Tài liệu Bộ đề thi Toán lớp 8 học kì 1 có đáp án năm học 2022- 2023 gồm 20 đề thi tổng hợp từ đề thi môn Toán 8 của các trường THCS trên cả nước đã được biên soạn đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi học kì 1 Toán lớp 8. Mời các bạn cùng đón xem:
Đề thi Học kì 1 Toán lớp 8 năm học 2022 - 2023 có đáp án (20 Đề) - Đề 1
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Môn: Toán 8
Thời gian làm bài: 90 phút
(Đề 1)
Bài 1: (1,5 điểm) Phân tích đa thức thành nhân tử:
a) x2 + xy –x – y
b) a2 – b2 + 8a + 16
Bài 2: (2 điểm) Tìm x, biết:
a) 4x(x + 1) + (3 – 2x)(3 + 2x) = 15
b) 3x(x – 20012) – x + 20012 = 0
Bài 3: (1,5 điểm) Cho biểu thức:
a) Tìm điều kiện của x để biểu thức A xác định
b) Rút gọn biểu thức A
Bài 4: (1 điểm) Tính tổng x4 + y4 biết x2 + y2 = 18 và xy = 5.
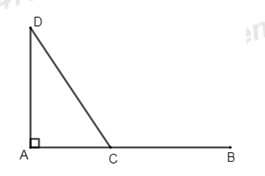
Bài 5: (4 điểm) Cho tam giác ABC vuông tại A (AB < AC) . M là trung điểm cạnh BC. Vẽ MD vuông góc với AB tại D và ME vuông góc với AC tại E.
a) Chứng minh tứ giác ADME là hình chữ nhật.
b) Chứng minh E là trung điểm của đoạn thẳng AC và tứ giác CMDE là hình bình hành.
c) Vẽ đường cao AH của tam giác ABC. Chứng minh tứ giác MHDE là hình thang cân
d) Qua A vẽ đường thẳng song song với DH cắt DE tại K. Chứng minh HK vuông góc với AC.
Đáp án và Hướng dẫn giải
Bài 1
a) x2 + xy –x – y = x(x + y) – (x + y) = (x + y)(x -1 ).
b) a2 – b2 + 8a + 16 = (a2 + 8a + 16) – b2 = (a + 4)2 – b2
= (a + 4 – b)(a + 4 + b).
Bài 2
a) 4x(x + 1) + (3 – 2x)(3 + 2x) = 15
⇔4x2 + 4x + (9 – 4x2) = 15
⇔ 4x2 + 4x + 9 – 4x2 = 15
⇔4x = 15 – 9
⇔4x = 6
⇔x = 3/2
b)3x(x – 20012) – x + 20012 = 0
⇔3x(x – 20012) – (x – 20012) = 0
⇔(x – 20012)(3x – 1) = 0
⇔x – 20012 = 0 hay 3x – 1 = 0
⇔x = 20012 hoặc x = 1/2
Bài 3
a) Ta có: x - 1 ≠ 0 ⇒ x ≠ 1
x2 - 1 = (x + 1)(x - 1) ≠ 0 ⇔ x ≠ -1 và x ≠ 1
x2 - 2x + 1 = (x - 1)2 ≠ 0 ⇔ x - 1 ≠ 0 ⇔ x ≠ 1
ĐKXĐ: x ≠ -1 và x ≠ 1
Bài 4
x4 + y4 = (x2 + y2)2-2x2 y2 = 182-2.52 = 274
Bài 5
a) Xét tứ giác ADME có:
∠(DAE) = ∠(ADM) = ∠(AEM) = 90o
⇒ Tứ giác ADME là hình chữ nhật (có ba góc vuông).
b) Ta có ME // AB ( cùng vuông góc AC)
M là trung điểm của BC (gt)
⇒ E là trung điểm của AC.
Ta có E là trung điểm của AC (cmt)
Chứng minh tương tự ta có D là trung điểm của AB
Do đó DE là đường trung bình của ΔABC
⇒ DE // BC và DE = BC/2 hay DE // MC và DE = MC
⇒ Tứ giác CMDE là hình bình hành.
c) Ta có DE // HM (cmt) ⇒ MHDE là hình thang (1)
Lại có HE = AC/2 (tính chất đường trung tuyến của tam giác vuông AHC)
DM = AC/2 (DM là đường trung bình của ΔABC) ⇒ HE = DM (2)
Từ (1) và (2) ⇒ MHDE là hình thang cân.
d) Gọi I là giao điểm của AH và DE. Xét ΔAHB có D là trung điểm của AB, DI // BH (cmt) ⇒ I là trung điểm của AH
Xét ΔDIH và ΔKIA có
IH = IA
∠DIH = ∠AIK (đối đỉnh),
∠H1 = ∠A1(so le trong)
ΔDIH = ΔKIA (g.c.g)
⇒ ID = IK
Tứ giác ADHK có ID = IK, IA = IH (cmt) ⇒ DHK là hình bình hành
⇒ HK // DA mà DA ⊥ AC ⇒ HK ⊥ AC

.................................................................................
Đề thi Học kì 1 Toán lớp 8 năm học 2022 - 2023 có đáp án (20 Đề) - Đề 2
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Môn: Toán 8
Thời gian làm bài: 90 phút
(Đề 2)
Câu 1: Gía trị của x thỏa mãn x2 + 16 = 8x là
A. x = 8 B. x = 4
C. x = -8 D. x= -4
Câu 2: Kết quả phép tính: 15 x3y5z : 3 xy2z là
A. 5x2 y3 B. 5xy
C. 3x2y3 D. 5xyz
Câu 3: Kết quả phân tích đa thức -x2 + 4x - 4 là:
A. -(x + 2)2 B. -(x - 2)2
C. (x-2)2 D. (x + 2)2
Câu 4: Mẫu thức chung của 2 phân thức: là:
A. 2(x - 1)2 B. x(x - 1)2
C. 2x(x-1) D. 2x (x-1)2
Câu 5: Điều kiện xác định của phân thức: 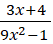
A. x≠1/3 B. x≠±1/3
C. x≠-1/3 D. x≠9
Câu 6: Khẳng định nào sau đây là sai:
A. Tứ giác có 2 đường chéo vuông góc với nhau tại trung điểm mỗi đường là hình thoi.
B. Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành
C. Hình chữ nhật có 2 đường chéo bằng nhau là hình vuông.
D. Hình chữ nhật có 2 đường chéo vuông góc với nhau là hình vuông.
Câu 7: Cho tứ giác MNPQ. Gọi E, F , G, H lần lượt là trung điểm các cạnh MN, NP, PQ, QM. Tứ giác EFGH là hình thoi nếu 2 đường chéo MP, NQ của tứ giác MNPQ:
A. Bằng nhau
B. Vuông góc
C. Vuông góc với nhau tại trung điểm mỗi đường
D. Cắt nhau tại trung điểm mỗi đường.
Câu 8: Độ dài 2 đường chéo của hình thoi lần lượt là 6 cm và 4 cm. Độ dài cạnh của hình thoi là:
A. 13 cm B. √13 cm
C. 52 cm D. √52 cm
Bài 1: (1 điểm) Phân tích thành nhân tử:
a) x2 + 4y2 + 4xy – 16
b) 5x2 - 10xy + 5y2
Bài 2: (2 điểm)
Cho biểu thức
a) Tìm điều kiện của x để biểu thức A xác định.
b) Rút gọn A
c) Tính giá trị của A khi x= -1
Bài 4: (1điểm )
Cho a + b = 1. Tính giá trị của các biểu thức sau:
M = a3 + b3 + 3ab(a2 + b2) + 6a2b2(a + b).
Bài 5: (4 điểm) Cho tam giác ABC vuông tại A (AB < AC).Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.
a) Chứng minh tứ giác AMIN là hình chữ nhật.
b) Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác ADCI là hình thoi.
c) Cho AC = 20cm, BC = 25cm.Tính diện tích ΔABC
d) Đường thẳng BN cắt cạnh DC tại K. Chứng minh:
Đáp án và Hướng dẫn giải
| 1.B | 2.A | 3.B | 4.D |
| 5.B | 6.C | 7.A | 8.B |
Bài 1
a) x2 + 4y2 + 4xy – 16 = (x + 2y)2 -16 = (x + 2y – 4)(x + 2y + 4).
b) 5x2 - 10xy + 5y2 = 5(x2 - 2xy + y2) = 5(x - y)2
Bài 2
a) x2 - 4 ≠ 0 ⇔ (x + 2)(x - 2) ≠ 0
ĐKXĐ: x ≠ - 2 và x ≠ 2
Bài 4: Ta có: a + b = 1
M = a3 + b3 + 3ab(a2 + b2) + 6a2b2(a + b)
= (a + b)3 - 3ab(a + b) + 3ab[(a + b)2 - 2ab] + 6a2 b2 (a + b)
= 1 - 3ab + 3ab(1 - 2ab) + 6a2 b2
= 1 - 3ab + 3ab - 6a2 b2 + 6a2 b2
= 1
Bài 5:
a) Xét tứ giác AMIN có:
∠(MAN) = ∠(ANI) = ∠(IMA) = 90o
⇒ Tứ giác AMIN là hình chữ nhật (có 3 góc vuông).
b) ΔABC vuông có AI là trung tuyến nên AI = IC = BC/2
do đó ΔAIC cân có đường cao IN đồng thời là đường trung tuyến
⇒ NA = NC.
Mặt khác ND = NI (t/c đối xứng) nên ADCI là hình bình hành
Lại có AC ⊥ ID (gt). Do đó ADCI là hình thoi.
c) Ta có: AB2 = BC2 – AC2 (định lí Py-ta-go)
= 252 – 202 ⇒ AB = √225 = 15 (cm)
Vậy SABC = (1/2).AB.AC = (1/2).15.20 = 150 (cm2)
d) Kẻ IH // BK ta có IH là đường trung bình của ΔBKC
⇒ H là trung điểm của CK hay KH = HC (1)
Xét ΔDIH có N là trung điểm của DI, NK // IH (BK // IH)
Do đó K là trung điểm của DH hay DK = KH (2)
Từ (1) và (2) ⇒ DK = KH = HC ⇒ DK/DC= 1/3.

.................................................................................
Đề thi Học kì 1 Toán lớp 8 năm học 2022 - 2023 có đáp án (20 Đề) - Đề 3
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Môn: Toán 8
Thời gian làm bài: 90 phút
(Đề 3)
Bài 1: (2 điểm)
a) Phân tích nhân tử
i) xy - 6y + 2x - 12
ii) 2x(y - z) + (z - y)(x + y)
b) Tìm x biết: x + 3 = (x + 3)2
Bài 2: (1 điểm) Rút gọn và tính giá trị của biểu thức:
Bài 3: (2 điểm) Cho biểu thức:
a) Tìm điều kiện xác định của biểu thức P.
b) Chứng minh giá trị của P luôn âm với x ≠ ±1
Bài 4: (1 điểm) Chứng minh rằng biểu thức
Bài 5: (4 điểm) Cho tam giác ABC vuông tại A. Gọi M, N lần lượt là trung điểm của hai cạnh AB và BC.
a) Gọi D là điểm đối cứng của A qua N. Chứng minh tứ giác ABCD là hình chữ nhật.
b) Lấy I là trung điểm của cạnh AC và E là điểm đối xứng của N qua I.
Chứng minh tứ giác ANCE là hình thoi.
c) Đường thẳng BC cắt DM và DI lần lượt tại G và G’. Chứng minh BG = CG’.
d) Cho AB = 6cm, AC = 8cm. Tính diện tích ΔDGG’.
Đáp án và Hướng dẫn giải
Bài 1
i) xy - 6y + 2x - 12
= (xy - 6y) + (2x - 12)
= y(x - 6) + 2(x - 6)
= (x - 6)(y + 2)
ii) 2x(y - z) + (z - y)(x + y)
= 2x(y - z) - (y - z)(x + y)
= (y - z)(2x - x - y)
= (y - z)(x - y)
b) x + 3 = (x + 3)2 ⇔ (x + 3)2 - (x + 3) = 0 ⇔ (x + 3)(x + 3 - 1) = 0
⇔ (x + 3)(x + 2) = 0
Vậy x = -3; x = -2
Bài 2: Điều kiện: x ≠ 1; x ≠ 0.
Bài 3
a) Ta có: x4 - 1 = (x2 + 1)(x2-1), trong đó : x2 + 1 > 0, với mọi x.
Vậy điều kiện : x2 – 1 ≠ 0
x2 – 1 = (x – 1)(x + 1) ≠ 0 ⇒ x ≠ ±1
b)
Do x2 + 1 > 0 với mọi x nên P < 0 với mọi x ≠ ±1
Bài 4
Do x2≥ 0 ∀ x ≠ ±1 nên Q=x2 + 1 ≥ 1 ∀ x ≠ ±1
Bài 5
a) Ta có: NB = NC (gt); ND = NA (gt)
⇒ Tứ giác ABDC là hình bình hành
có ∠A = 90o (gt) ⇒ ABDC là hình chữ nhật.
b) Ta có: AI = IC (gt); NI = IE (gt)
⇒ AECN là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).
mặt khác ΔABC vuông có AN là trung tuyến nên AN = NC = BC/2.
Vậy tứ giác AECN là hình thoi.
c) BN và DM là 2 đường trung tuyến của tam giác ABD; BN và MD giao nhau tại G nên G là trọng tâm tam giác ABD.
Tương tự G’ là trọng tâm của hai tam giác ACD
⇒ BG = BN/3 và CG’ = CN/3 mà BN = CN (gt) ⇒ BG = CG’
d) Ta có: SABC = (1/2).AB.AC = (1/2).6.6 = 24 (cm2)
Lại có: BG = GG’ = CG’ (tính chất trọng tâm)
⇒ SDGB = SDGG' = SDG'C = 1/3 SBCD
(chung đường cao kẻ từ D và đáy bằng nhau)
Mà SBCD = SCBA (vì ΔBCD = ΔCBA (c.c.c))
⇒SDGG' = 24/3 = 8(cm2)
.................................................................................
Đề thi Học kì 1 Toán lớp 8 năm học 2022 - 2023 có đáp án (20 Đề) - Đề 4
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Môn: Toán 8
Thời gian làm bài: 90 phút
(Đề 4)
Câu 1: Kết quả của phép tính: (2x2 – 32) : (x – 4 ) là:
A. 2(x – 4) B. 2(x + 4)
C. x + 4 D. x – 4
Câu 2: Mẫu thức chung của 2 phân thức là:
A. x(x + 2)2 B. 2(x + 2)2
C. 2x(x + 2)2 D. 2x(x + 2)
Câu 3: Kết quả của phép tính là
Câu 4: Tập hợp các giá trị của x để 3x2=2x là :
Câu 5: Với x = 105 thì giá trị của biểu thức x2-10x + 25 là:
A. 1000 B. 1025
C. 10000 D. 10025
Câu 6: Trong các khẳng định sau, khẳng định nào sai?
A. Hình thang có 2 cạnh bên bằng nhau là hình thang cân
B. Tứ giác có 2 cạnh đối song song là hình thang
C. Hình thang cân có 1 góc vuông là hình chữ nhật
D. Hình chứ nhật có 2 đường chéo vuông góc là hình vuông.
Câu 7: Cho hình chữ nhật ABCD có AB = 6 cm, BC = 8cm. M, N, P, Q là trung điểm các cạnh của hình chữ nhật. Tổng diện tích các tam giác có trong hình là:
A. 4 cm2 B. 6 cm2
C. 12 cm2 D. 24 cm2
Câu 8: Trong hình dưới, biết ABCD là hình thang vuông, tam giác BMC đều. Số đo của góc ABC là:
A. 60o B. 130o
C. 150o D. 120o
Bài 1: (2 điểm) Phân tích thành nhân tử
a) x6 – x4 + 2x3 + 2x2
b) 4x4 + y4
Bài 2: (2 điểm) Cho biểu thức :
a) Rút gọn biểu thức P
b) Tính giá trị biểu thức P với x = 1/2
Bài 3: (1 điểm)
Chứng tỏ rằng đa thức : P = x2 - 2x + 2 luôn luôn lớn hơn 0 với mọi x
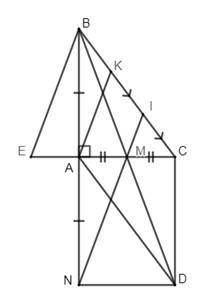
Bài 4: (3 điểm) Cho ΔABC cân tại A có AB = 5cm; BC = 6cm. Kẻ phân giác trong AM (M ∈ BC) . Gọi O là trung điểm của AC và K là điểm đối xứng của M qua O.
a) Tính diện tích tam giác ABC.
b) Tứ giác ABMO là hình gì? Vì sao?
c) Để tứ giác AMCK là hình vuông thì tam giác ABC phải có thêm điều kiện gì?
Đáp án và Hướng dẫn giải
| 1.B | 3.C | 5.C | 7.D |
| 2.C | 4.B | 6.A | 8.D |
Bài 1
a) x6 – x4 + 2x3 + 2x2
= x2(x4 – x2 + 2x + 2)
= x2[x2(x2 – 1) + 2(x + 1)]
= x2. [x2.(x -1).(x + 1) + 2(x+ 1)]
= x2 (x+ 1).[x2(x- 1)+ 2]
= x2(x + 1)(x3 – x2 + 2)
= x2(x + 1)[(x3 + 1) – (x2 – 1)]
= x2(x + 1).[(x + 1).(x2 – x + 1) - (x - 1).(x + 1)]
= x2(x + 1)(x + 1)( x2 – x + 1 – x + 1)
= x2(x + 1)2(x2 – 2x + 2).
b) 4x4 + y4 = 4x4 + 4x2y2 + y4 - 4x2y2
= (2x2 + y2)2 - (2xy)2
= (2x2 + y2 + 2xy)(2x2 + y2 - 2xy)
Bài 2
a) Ta có: 2x2 + 8 = 2(x2 + 4).
8 – 4x + 2x2 – x3
= (8 – x3) - ( 4x - 2x2)
= (2 – x).(4 + 2x + x2) - 2x.(2 - x)
= (2 – x).(4 + 2x + x2 – 2x)
= (2 - x). (4 + x2 )
* Do đó:
b) Tại 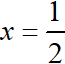
vào biểu thức rút gọn của P ta được:
Bài 3
P = x2 - 2x + 2 = (x – 1)2 + 1
Do (x – 1)2 ≥ 0 ∀x nên (x – 1)2 + 1 ≥ 1 ∀x
Vậy P luôn lớn hơn 0 với mọi x.
Bài 4: (3 điểm)
a) Vì M là trung điểm của BC nên:
BM = BC/2 = 6/2 = 3(cm)
Tam giác ABC cân tại A, lại có AM là đường phân giác nên AM cũng là đường cao. Do đó tam giác AMB vuông tại M.
Suy ra: AM2 = AB2 - BM2 (Định lí Pytago)
= 52 - 32 = 16(cm)
Suy ra AM = 4cm
b) ΔAMC vuông tại M có MO là đường trung tuyến nên OM = OA.
Suy ra ∠OAM = ∠OMA ( ΔAMO cân tại O)
Lại có ∠OAM = ∠MAB (AM là tia phân giác góc BAC)
Suy ra ∠OMA = ∠MAB
Mà đây là 2 góc ở vị trí so le trong
Suy ra OM // AB
Vậy tứ giác ABMO là hình thang.
c) Tứ giác AMCK có OA = OC; OM = OK nên tứ giác AMCK là hình bình hành . Lại có ∠AMC = 90o (chứng minh trên) nên tứ giác AMCK là hình chữ nhật.
Hình chữ nhật AMCK là hình vuông
⇔ AM = MC = BM
⇔ AM = BC/2
⇔ ΔABC vuông cân tại A.
Đề thi Học kì 1 Toán lớp 8 năm học 2022 - 2023 có đáp án (20 Đề) - Đề 5
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Môn: Toán 8
Thời gian làm bài: 90 phút
(Đề 5)
A. TRẮC NGHIỆM: (2,5 điểm)
Câu 1. Biểu thức còn thiếu của hằng đẳng thức: là:
A. 4 xy
B. - 4xy
C. 2 xy
D. -2 x y
Câu 2. Kết quả của phép nhân: bằng:
A.
B.
C.
D.
Câu 3. Kết quả của rút gọn biểu thức :
A. x2 + 4x - 2
B. x2 - 4x + 4
C. x2 + 4x + 4
D. x2 - 4x - 4
Câu 4 . Phân thức nghịch đảo của phân thức là phân thức nào sau đây :
A.
B.
C.
D.
Câu 5 . Phân thức đối của phân thức là :
A.
B.
C.
D. Cả A, B, C đều đúng
Câu 6 . Hình nào sau đây có 4 trục đối xứng ?
A. Hình thang cân
B. Hình bình hành
C. Hình chữ nhật
D. Hình vuông
Câu 7 . Cho hình thang ABCD có AB/ / CD, thì hai cạnh đáy của nó là :
A. AB ; CD
B. AC ;BD
C. AD; BC
D. Cả A, B, C đúng
Câu 8 . Cho hình bình hành ABCD có số đo góc , vậy số đo góc D bằng:
A. 700
B. 750
C. 800
0.850
Câu 9. Một miếng đất hình chữ nhật có độ dài 2 cạnh lần lượt là 4m và 6m ; người ta làm bồn hoa hình vuông cạnh 2m, phần đất còn lại để trồng cỏ, hỏi diện tích trồng cỏ là bao nhiêu m2?
A. 24
B. 16
C. 20
D. 4
Câu 10. Số đo một góc trong của ngũ giác đều là bao nhiêu độ ?
A. 1200
B. 1080
C. 720
D. 900
B. TỰ LUẬN (7,5 điểm)
Bài 1 (1,25 điểm) Phân tích các đa thức sau thành nhân tử
a)
b)
Bài 2 (1,25 điểm) Cho 2 đa thức : và B=2 x+1
a) Tìm đa thức thương và dư trong phép chia A cho B
b) Tìm m để A chia hết cho B
Bài 3. (1,5 điểm) Thực hiện rút gọn các biểu thức:
a)
b)
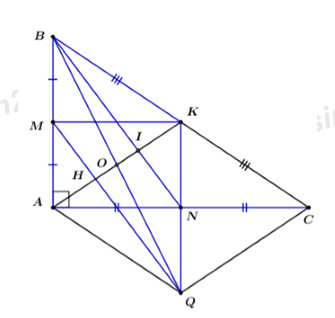
Bài 4. (3,5 điểm) Cho tam giác ABC, gọi D, E, F lần lượt là trung điểm của các cạnh AB, AC, BC; và M, N, P, Q theo thứ tự là trung điểm các đoạn thẳng DA, AE, EF, FD.
a) Chứng minh: EF là đường trung bình của tam giác ABC
b) Chứng minh: Các tứ giác DAEF; MNPQ là hình bình hành
c) Khi tam giác ABC vuông tại A thì các tứ giác DAEF; MNPQ là hình gì ? Chứng minh?
d)Tìm điều kiện của tam giác ABC để tứ giác MNPQ là hình vuông?
Đề thi Học kì 1 Toán lớp 8 năm học 2022 - 2023 có đáp án (20 Đề) - Đề 6
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Môn: Toán 8
Thời gian làm bài: 90 phút
(Đề 6)
A. TRẮC NGHIỆM (2,5 điểm)
Câu 1. Vế phải của hằng đẳng thức: . . là:
A.
B.
C.
D.
Câu 2 Kết quả của phép chia bằng :
A.
B. 3 xy
C. -3 xy
D.
Câu 3: Rút gọn biểu thức được kết quả nào sau đây?
A.
B.
C.
D.
Câu 4 . Phân thức đối của phân thức là phân thức :
A.
B.
C.
D.
Câu 5 . Điều kiện xác định của phân thức là
A.
B.
C.
D.
Câu 6. Hình nào sau đây không có trục đối xứng ?
A. Hình thang cân
B. Hình bình hành
C. Hình chữ nhật
D. Hình vuông
Câu 7. Cho hình thang ABCD có AB // CD, thì độ dài đường trung bình của hình thang được tính theo công thức nào sau đây ?
A.
B.
C.
D.
Câu 8 . Tứ giác ABCD có số đo góc A =750 ; góc B =1150 ; góc C =1000. Vậy số đo góc D bằng
A. 700
B. 750
C. 800
D. 850
Câu 9. Một hình vuông có diện tích bằng diện tích một hình chữ nhật có chiều rộng 2 m và chiều dài 8 m, độ dài cạnh hình vuông là:
A. 2 m
B. 4 m
C. 6 m
D. 8 m
Câu 10. Hình đa giác lồi 6 cạnh có bao nhiêu đường chéo
A. 6
B. 7
C. 8
D. 9
B. TỰ LUẬN (7,5 điểm)
Bài 1: (1.5 điểm) Phân tích các đa thức sau thành nhân tử:
a)
b)
Bài 2: (2,0 điểm)
Bài 3: (3,5 điểm ) Cho trung tuyến AD, gọi E là trung điểm của AB,
là điểm đối xứng của điểm D qua E.
1. Chứng minh: Tứ giác ANBD là hình bình hành
2. Tìm điều kiện của tam giác ABC để tứ giác ANBD là :
a) Hình chữ nhật
b) Hình thoi
c) Hình vuông
3. Gọi M là giao điểm của NC với AD, chứng minh
Bài 4 (0,5 điểm) Cho x, y , z là ba số khác 0 và . Tính giá trị của biểu thức :
Đề thi Học kì 1 Toán lớp 8 năm học 2022 - 2023 có đáp án (20 Đề) - Đề 7
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Môn: Toán 8
Thời gian làm bài: 90 phút
(Đề 7)
A. TRẮC NGHIỆM.
Câu 1 . Vế còn lại của hằng đẳng thức : là
Câu 2. Phân tích đa thức : thành nhân tử ta được kết quả là:
Câu 3. Kết quả của phép tính: bằng :
Câu 4. Điều kiện xác định của phân thức là :
D. Cả B và C
Câu 5. Phân thức nghịch đảo của phân thức là :
Câu 6. Hình nào sau đây có 2 trục đối xứng:
A. Hình thang cân
B. Hình bình hành
C. Hình chữ nhật
D. Hình vuông
Câu 7. Hình bình hành ABCD cần có thêm điều kiện gì để trở thành hình thoi
A. Hai đường chéo vuông góc
B. Hai cạnh liên tiếp bằng nhau
C. Có một góc vuông
D. Cả A và B đều đúng
Câu 8. Hình thang MNPQ có 2 đáy MQ = 12 cm, NP = 8 cm thì độ dài đường trung bình
của hình thang đó bằng:
A. 8 cm
B. 10 cm
C. 12 cm
D. 20 cm
Câu 9. Diện tích hình vuông tăng lên gấp 4 lần, hỏi độ dài mỗi cạnh hình vuông đã tăng
lên gấp mấy lần so với lúc ban đầu ?
A.2
B. 4
C. 8
D. 16
Câu 10. Một hình thoi có độ dài hai đường chéo lân lượt bằng 8 cm và 6 cm, hỏi độ dài
cạnh hình thoi bằng bao nhiêu cm
A. 5cm
B. 10 cm
C. 12 cm
D. 20 cm
B. TỰ LUẬN : (7,5 điểm)
Bài 1 : (1,5 điểm) Phân tích đa thức thành nhân tử
Bài 2:(1,0 điểm) Đặt phép chia để tính
Bài 3:(1,5 điểm) Rút gọn biểu thức
Bài 4 : (3,5 điểm) Cho tam giác ABC vuông tại A, AB < AC. Gọi D, E, F lần lượt là trung điểm của các cạnh AB, AC, BC.
1. Chứng minh : Tứ giác FDEC là hình bình hành
2. Chứng minh : AF = DE
3. Gọi K là hình chiếu của điểm A trên cạnh BC, chứng minh tứ giác KDEF là hình thang cân.
Đề thi Học kì 1 Toán lớp 8 năm học 2022 - 2023 có đáp án (20 Đề) - Đề 8
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Môn: Toán 8
Thời gian làm bài: 90 phút
(Đề 8)
A. TRẮC NGHIỆM (2 Điểm) Chọn câu trả lời đúng cho mỗi câu sau:
Câu 1. Trong hằng đẳng thức Số hạng còn thiếu chỗ .........là:
A. xy
B. 2xy
C. -xy
D. -2xy
Câu 2. Phân thức bằng:
D. Cả A, B, C đúng
Câu 3. Rút gọn phân thức , ta được:
A. x+2
B. x-2
C. x
D. -2
Câu 4. Điều kiện của biến x để giá trị của biểu thức xác định là:
A. Mọi x
B.
C.
D.
Câu 5. Tứ giác có hai đường chéo bằng nhau và giao nhau tại trung điểm mỗi đường là hình gì?
A. Hình chữ nhật
B. Hình thoi
Câu 6. Hình chữ nhật có mấy trục đối xứng?
A. 1
B. 2
C. 3
D. 4
Câu 7. Hình nào sau đây là đa giác đều
A. Hình chữ nhật
B. Hình thoi
C. Hình vuông
D. Cả A, B, C đúng
Câu 8. Tăng độ dài cạnh hình vuông lên ba lần thì diện tích của nó tăng mấy lần?
A. 3
B. 6
C. 9
D. Một số khác
B. TỰ LUẬN (8 điểm)
Câu 1. (1,5 điểm)
Phân tích các đa thức thành nhân tử:
Câu 2. (1,5 điểm)
Tính:
Câu 3. (1.5 điểm)
Cho biểu thức
a. Rút gọn M
b. Tìm các giá trị nguyên của x để M có giá trị nguyên
Câu 4 .
Hình thang . Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a. Chứng minh các tứ giác ABPD, MNPQ là hình bình hành
b. Tìm điều kiện của hình thang ABCD để MNPQ là hình thoi.
c. Gọi E là giao điểm của BD và AP. Chứng minh ba điểm Q, N, E thẳng hàng
Đề thi Học kì 1 Toán lớp 8 năm học 2022 - 2023 có đáp án (20 Đề) - Đề 9
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Môn: Toán 8
Thời gian làm bài: 90 phút
(Đề 9)
I. TRẮC NGHIỆM (3 Điểm)
Hãy chọn ý trả lời đúng trong các câu sau đây. Ví dụ: Nếu chọn ý \mathbf{A} của câu \mathbf{1} thì ghi là 1.A
Câu 1: Viết đa thức dưới dạng bình phương của một tổng ta được kết quả nào sau đây:
Câu 2: Phân tích đa thức: thành nhân tử ta được kết quả nào sau đây:
B. 5 x(x-2)
D. 5 x(2-x)
Câu 3: Hình chữ nhật ABCD có . Khi đó, diện tích hình chữ nhật ABCD là:
B. 40
C. 20
D. 3
Câu 4: Giá trị của biểu thức khi x=-2 là:
A. 0
B. -1
C. 4
D. Không xác định
Câu 5: Mẫu thức chung của hai phân thức: là:
Câu 6: Hiệu của biểu thức bằng:
D. 1 kết quả
Câu 7: Phân thức sau khi rút gọn được:
Câu 8: Cho . Đa thức P là:
Câu 9: Tam giác ABC vuông tại A. Gọi M là trung điểm AB, N là trung điểm BC; biết thì MN bằng:
A. 1,5cm
B. 2,5 cm
C. 2cm
D. 5 cm
Câu 10: Trong tất cả các tứ giác đã học, hình có 2 trục đối xứng là:
A. Hình thang
B. Hình thang cân
C. Hình chữ nhật
D. Hình vuông
Câu 11: Một hình thang có đáy lớn bằng 10 cm đường trung bình của hình thang bằng 8 cm. Đáy nhỏ của hình thang có độ dài là:
A. 6 cm
B. 8 cm
C. 10 cm
D. 12 cm
Câu 12: Hai đường chéo hình thoi có độ dài 8 cm và 10 cm. Cạnh của hình thoi có độ dài là:
A. 6 cm
D. 9cm
II. TỰ LUẬN (7 Điểm)
Bài 1: (1,5đ) Phân tích đa thức thành nhân tử:
a/ 2x-6 y
Bài 2: (2đ) Thực hiện phép tính:
Bài 3: (0,5 điểm) Tìm giá trị của x để giá trị phân thức bằng 0 .
Bài 4: (3đ) Cho hình bình hành ABCD có AB = AC. Gọi I là trung điểm của BC, E là điểm
đối xứng của A qua I.
a) Chứng minh ABEC là hình thoi.
b) Chưng minh D, C, E thẳng hàng.
c) Tính số đo góc DAE.
d) Tìm điều kiện của tam giác ADE để tứ giác ABEC trở thành hình vuông
Đề thi Học kì 1 Toán lớp 8 năm học 2022 - 2023 có đáp án (20 Đề) - Đề 10
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Môn: Toán 8
Thời gian làm bài: 90 phút
(Đề 10)
Bài 1 (2 điểm): Thực hiện phép tính
|
a) |
b) |
Bài 2 (2,5 điểm):
1. Phân tích các đa thức sau thành nhân tử
|
a) |
b) |
2. Tìm x:
Bài 3 (1 điểm): Trong một cuộc thi, học sinh cần trả lời 50 câu hỏi trắc nghiệm, mỗi câu trả lời đúng được 5 điểm, mỗi câu trả lời sai (hoặc không trả lời) bị trừ 2 điểm. An đã tham gia cuộc thi trên và đã ghi được tổng cộng là 194 điểm. Hỏi An trả lời đúng mấy câu?
Bài 4: (0,75 điểm)
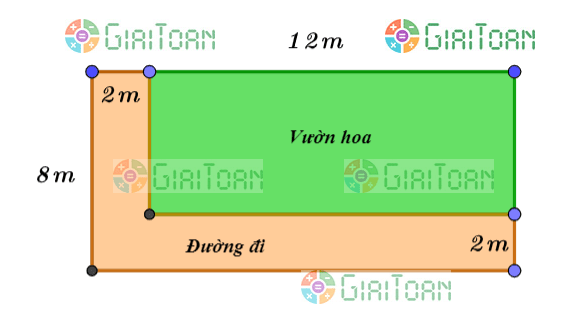
Bác Bình có một miếng đất hình chữ nhật có chiều dài là 12m, chiều rộng là 8m. Bác dự định làm một vườn hoa, và chừa ra một phần đường đi (như hình vẽ), để tiện cho việc chăm sóc các cây. Bác đã thực hiện việc lát những viên gạch chống trượt hình vuông có cạnh 40cm trên phần đường đi. biết rằng diện tích các mối nối và sự hao hụt là không đáng kể.
Em hãy tính xem bác Bình đã dùng bao nhiêu viên gạch cho việc lát đường đi trên.
Bài 5 (0,75 điểm): Theo cuộc tổng điều tra dân số và nhà ở của Thành phố Hồ Chí Minh giai đoạn 2009 - 2019, dân số thành phố hiện nay (tính đến ngày 11/10/2019) trong khoảng 8990000 người, với tỷ lệ tăng dân số hàng năm là khoảng 2%/1 năm. Hỏi nếu tỷ lệ tăng dân số trung bình hàng năm vẫn giữ như mức trên thì sau 2 năm dân số của Thành phố là bao nhiêu người?
Bài 6 (2,5 điểm): Cho ∆ABC cân tại A có D; E; M lần lượt là trung điểm của AB; AC; BC
a) Chứng minh: BDEC là hình thang cân.
b) Gọi K là đối xứng của M qua E. Chứng minh: AMCK là hình chữ nhật.
c) Gọi N là giao điểm của AM và DE. Chứng minh: B; N; K thẳng hàng.
Bài 7 (0,5 điểm): Một công nhân của một công ty được trả lương cơ bản là 250000 đồng cho một ngày làm việc bình thường trong tháng, nếu có tăng ca vào thứ 7 hoặc chủ nhật thì mức lương tính riêng cho những ngày này tăng thêm 50% trên mức lương cơ bản. Biết rằng trong tháng 11/2019 (có 30 ngày) công ty có rất nhiều công việc cần giải quyết nên anh công nhân trên đã quyết định làm thêm tất cả các ngày thứ 7, chủ nhật trong tuần của tháng để giúp công ty và ngày 30/11 rơi vào ngày thứ 7. Em hãy tính xem sau tháng 11, anh công nhân nhận được bao nhiêu tiền lương?
Đề thi Học kì 1 Toán lớp 8 năm học 2022 - 2023 có đáp án (20 Đề) - Đề 11
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Môn: Toán 8
Thời gian làm bài: 90 phút
(Đề 11)
Câu 1 (2 điểm):
1. Phân tích đa thức thành nhân tử
| a. |
b. |
2. Tìm x biết:
Câu 2 (2 điểm): Thực hiện phép tính
| a. |
b. |
| c. |
d. |
Câu 3 (2 điểm)
a) Tính giá trị nhỏ nhất của biểu thức:
b) Tính giá trị của biểu thức
Biết a, b, c thỏa mãn:
Câu 4 (3 điểm): Cho tam giác ABC cân tại A có đường cao AH. Gọi M là trung điểm của AC, D đối xứng với H qua M. Gọi K là giao điểm của AH và BD, I là giao điểm của CK và DH. Chứng minh rằng:
a) Tứ giác DCHA là hình chữ nhật.
b) Tứ giác BHDA là hình bình hành.
c) KB = 3IK.
Câu 5 (1 điểm): Bác Hùng một mảnh đất hình chữ nhật, bác muốn cải tạo mảnh đất để làm sân lát bằng gạch đỏ và trồng hoa xen kẽ. Tính diện tích phần trồng hoa và số tiền mua hoa. Biết diện tích trồng hoa bằng diện tích mảnh đất và bác phải dùng hết 96 viên gạch vuông kích thước 60cm x 60cm để lát sân, giá loại hoa bác trồng là 40000 đồng/m2
Đề thi Học kì 1 Toán lớp 8 năm học 2022 - 2023 có đáp án (20 Đề) - Đề 12
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Môn: Toán 8
Thời gian làm bài: 90 phút
(Đề 12)
Câu 1 (2 điểm): Phân tích đa thức thành nhân tử
| a) |
b) |
| c) |
|
Câu 2 (2 điểm): Thực hiện phép tính
| a) |
b) |
| c) |
d) |
Câu 3 (2 điểm)
a) Tìm x biết:
b) Tính giá trị nhỏ nhất của biểu thức:
Câu 4 (3 điểm) Cho tam giác ABC cân tại A có AH là đường cao. Gọi M là trung điểm của cạnh AB. Gọi E là điểm đối xứng của H qua M, F là điểm đối xứng của A qua H. Gọi K là hình chiếu của H lên cạnh FC. Gọi I, Q lần lượt là trung điểm của HK, KC.
a) Tính diện tích tam giác ABC biết AH = 6cm, BC = 8cm.
b) Chứng minh tứ giác AHBE là hình chữ nhật.
c) Chứng minh tứ giác ABFC là hình thoi.
d) Chứng minh BK vuông góc IF.
Câu 5 (1 điểm) Tính giá trị biểu thức:
Biết a, b, c là ba số khác 0 thỏa mãn điều kiện và
Đề thi Học kì 1 Toán lớp 8 năm học 2022 - 2023 có đáp án (20 Đề) - Đề 13
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Môn: Toán 8
Thời gian làm bài: 90 phút
(Đề 13)
Câu 1 (2 điểm): Phân tích đa thức thành nhân tử
|
a. |
b. |
|
c. |
d. |
Câu 2 (2 điểm): Cho biểu thức:
a) Rút gọn biểu thức A
b) Tính giá trị x biết A = 4
Câu 3 (2 điểm):
1. Tìm x:
|
a) |
b) |
2.
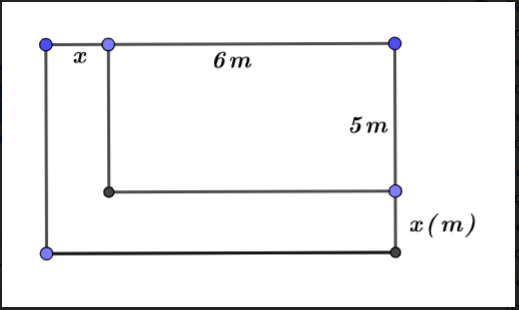
Người ta làm một lối đi theo chiều dài và chiều rộng của một mảnh vườn hình chữ nhật (như hình vẽ). Tính chiều rộng của lối đi, biết lối đi có diện tích bằng 26m2
Câu 4 (1 điểm) Bà Hoa dự định mua một chiếc xe máy với giá 30 triệu đồng, vì không đủ tiền nên bà mua trả góp trong vòng một năm với lãi suất là 6% trên một năm. Ban đầu bà trả trước 20% giá trị chiếc xe đó. Biết rằng số tiền mỗi tháng bà phải trả là như nhau và tiền lãi cửa hàng chỉ tính trên số tiền trả sau. Hỏi mỗi tháng bà Hoa phải trả cho cửa hàng bao nhiêu tiền?
Câu 5 (2 điểm) Cho tam giác ABC nhọn có trực tâm H. Các đường vuông góc với AB tại B và vuông góc với AC tại C cắt nhau tại D.
a) Chứng minh tứ giác BDCH là hình bình hành.
b) Chứng minh BAC + BHC = 180°.
c) Chứng minh bốn điểm A, B, D, C cách đều một điểm
Câu 6 (1 điểm) Cho hai số dương và b thỏa mãn . Tính giá trị của biểu thức:
Đề thi Học kì 1 Toán lớp 8 năm học 2022 - 2023 có đáp án (20 Đề) - Đề 14
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Môn: Toán 8
Thời gian làm bài: 90 phút
(Đề 14)
Bài 1 (1,5 điểm) Phân tích các đa thức sau thành nhân tử:
Bài 2 (3 điểm) Thực hiện phép tính:
a)
b)
c)
d)
Bài 3 (1,5 điểm)
a) Thực hiện phép chia đa thức cho đa thức .
b) Gọi Q là thương của phép chia A cho B. Chứng minh luôn nhận giá trị dương với mọi
Bài 4 (3 điểm) Cho vuông tại A . Gọi thứ tự là trung điểm của và .
a) Chứng minh và là hình thang vuông.
b) Qua kẻ đường thẳng song song với , cắt tia tại . Chứng minh là hình thoi.
c) cắt tại , cắt tại . Biết . Tính độ dài .
Bài 5 (1 điểm) Trong hình vẽ sau, hai địa điểm A và B cách nhau . Một xe ô tô khởi hành từ B đến A với vận tốc . Cùng lúc đó, một xe đạp điện cũng khởi hành từ A trên đoạn đường vuông góc với AB với vận tốc . Gọi C, D thứ tự là vị trí của xe ô tô và xe đạp điện vào thời điểm t(h) sau khi khởi hành. Giả sử vận tốc của hai xe không thay đổi trong quá trình di chuyển.
a) Viết biểu thức đại số biểu diễn độ dài theo .
b) Hỏi sau bao lâu (tính từ lúc khởi hành) khoảng cách là ngắn nhất? Giải thích.
Đáp án đề kiểm tra Học kì Toán 8
Bài 1:
a)
b)
Bài 2:
Bài 3:
a) Thực hiện phép chia đa thức cho đa thức .
b) Ta có:
Vì
Bài 4:
a) Vì lần lượt là trung điểm của và (gt)
là đường trung bình của (dấu hiệu nhận biết đường trung bình của tam giác)
(tính chất đường trung bình của tam giác)
Ta có: tứ giác là hình thang (dấu hiệu nhận biết hình thang)
Lại có: hình thang là hình thang vuông (dấu hiệu nhận biết hình thang vuông)
b)Ta có: mà tứ giác là hình bình hành (dấu hiệu nhận biết hình bình hành)
(tính chất hình bình hành)
Từ và , lại có là hình bình hành (dấu hiệu nhận biết hình bình hành)
Mặt khác, xét có là trung tuyến (gt) suy ra (trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy)
Mà
hình bình hành là hình thoi (dấu hiệu nhận biết hình thoi)
c)Gọi là giao điểm của và
Vì là hình bình hành (cmt)
(tính chất hình bình hành) (so le trong)
Xét và có:
(cmt)
(đối đỉnh)
(2 cạnh tương ứng)
Xét có:
(do )
là trung điểm của
là trung điểm của (trong tam giác, đường thẳng đi qua trung điểm của cạnh thứ nhất và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba)
(tính chất trung điểm của đoạn thẳng)
Vì là hình thoi (cmt) mà là trung điểm của và là trung điểm của (tính chất hình thoi)
Xét có:
(do )
là trung điểm của
là trung điểm của (trong tam giác, đường thẳng đi qua trung điểm của cạnh thứ nhất và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba)
(tính chất trung điểm của đoạn thẳng)
Từ và
Xét có: (trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy)
Ta có:
Do là hình thoi (cmt) và là giao điểm của hai đường chéo và (tính chất hình thoi)
Mà
Từ và là hình bình hành (dấu hiệu nhận biết hình bình hành)
là trung điểm của (tính chất hình bình hành)
(tính chất trung điểm)
Lại có
Mà
Bài 5:
a) Quãng đường BC mà ô tô đi được trong thời gian t giờ là: 40t (km)
Vậy độ dài của quãng đường AC là:
Quãng đường AD mà xe đạp điện đi được trong thời gian t giờ là:
b) Áp dụng định lí Py-ta-go cho tam giác ADC vuông tại A ta có:
Để độ dài đoạn DC ngắn nhất thì đạt giá trị nhỏ nhất. Ta có :
nên DC đạt giá trị nhỏ nhất
Vậy sau khi 2 xe khởi hành được 2 giờ thì khoảng cách CD ngắn nhất.
Đề thi Học kì 1 Toán lớp 8 năm học 2022 - 2023 có đáp án (20 Đề) - Đề 15
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Môn: Toán 8
Thời gian làm bài: 90 phút
(Đề 15)
Bài 1 (2 điểm) Phân tích các đa thức sau thành nhân tử:
a)
b)
c)
Bài 2 (1,5 điểm)
a. Làm tính chia:
b. Rút gọn biểu thức:
Bài 3 (2,5 điểm) Cho biểu thức: (với )
a) Rút gọn biểu thức .
b) Tính giá trị của khi
c) Tìm giá trị nguyên của để có giá trị nguyên.
Bài 4 (3,5 điểm) Cho vuông tại , gọi là trung điểm của . Gọi là điểm đối xứng với qua .
a) Chứng minh tứ giác là hình bình hành.
b) Gọi là điểm đối xứng với qua . Chứng minh tứ giác là hình chữ nhật.
c) Kéo dài cắt tại . Vẽ đường thẳng qua song song với cắt ở. Chứng minh:
d) Qua kẻ đường thẳng song song với cắt kéo dài tại . Tam giác cần có thêm điều kiện gì để tứ giác là hình vuông.
Bài 5 (0,5 điểm) Cho thỏa mãn: . Tính giá trị của biểu thức:
Đáp án đề kiểm tra Học kì Toán 8
Bài 1:
Bài 2:
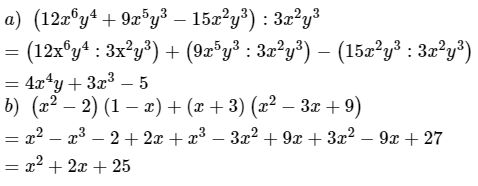
Bài 3:
Với thay vào A ta có: .
c) Ta có: , để nguyên
|
|
1 |
-1 |
3 |
-3 |
9 |
-9 |
|
|
-2 (tm) |
-4 (tm) |
0 (tm) |
-6 (tm) |
6 (tm) |
-12 (tm) |
Vậy với thì nguyên.
Bài 4:
a) Ta có: Vì và đối xứng với nhau qua (gt)(tính chất hai điểm đối xứng với nhau qua 1 điểm)
Xét tứ giác ta có:
Tứ giác là hình bình hành (dhnb)
b)Vì đối xứng với qua (gt)
(tính chất)
Lại có là hình bình hành (cmt)
(tính chất)
là hình bình hành (dhnb)
Mặt khác,
hình bình hành là hình chữ nhật (dhnb) (đpcm)
c)Xét có: (do )
là đường trung bình của (định lý)
(tính chất)
Xét có: (do )
(gt)
là đường trung bình của (dhnb)
(tính chất)
Mà (do )
d)Vì Tứ giác là hình thang (dấu hiệu nhận biết hình thang)
Lại có: K là trung điểm của BI (cmt) và là trung điểm của EM (trong hình thang, nếu một đường thẳng đi qua trung điểm của cạnh bên thứ nhất và song song với cạnh đáy thì đi qua trung điểm của cạnh bên thứ hai)
Xét tứ giác có hai đường chéo BN và EM cắt nhau tại trung điểm A của mỗi đường.
là hình bình hành (dhnb)
Mà hình bình hành BENM là hình thoi (dhnb)
Để hình thoi BENM là hình vuông khi và chỉ khi .
Bài 5:
Theo đề bài ta có:
Vậy
Đề thi Học kì 1 Toán lớp 8 năm học 2022 - 2023 có đáp án (20 Đề) - Đề 16
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Môn: Toán 8
Thời gian làm bài: 90 phút
(Đề 16)
Bài 1 (2 điểm)
a) Phân tích đa thức sau thành nhân tử:
b) Tính nhanh giá trị của biểu thức: tại
c) Tìm x, biết:
Bài 2 (2 điểm)
a) Rút gọn biểu thức:
b) Thực hiện phép tính:
c) Thực hiện phép tính:
Bài 3 (1,5 điểm)Cho hai đa thức và .
a) Thực hiện phép chia A cho B.
b) Tìm các giá trị nguyên của x để giá trị của đa thức A chia hết cho giá trị của đa thức B.
Bài 4 (4 điểm) Cho cân tại A. Gọi lần lượt là trung điểm của và .
a) Chứng minh tứ giác là hình thang.
b) Trên tia đối của tia lấy điểm sao cho là trung điểm của cạnh . Chứng minh tứ giác là hình thoi.
c) Qua A vẽ đường thẳng vuông góc với cắt tia tại . Chứng minh .
d) Vẽ , gọi I là trung điểm của AN. Trên tia đối của tia BH lấy điểm M sao cho B là trung điểm của HM. Chứng minh:
Bài 5 (0,5 điểm)
Cho là ba số thỏa mãn điều kiện:
Tính:
Đáp án đề kiểm tra Học kì Toán 8
Bài 1:
Thay vào đa thức trên ta được: .
Vậy
Bài 2:
Bài 3:
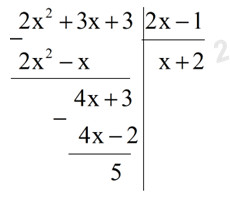
Để A chia hết cho B Ta có:
|
|
1 |
-1 |
5 |
-5 |
|
|
1 |
0 |
3 |
-2 |
Vậy thì chia hết cho .
Bài 4:
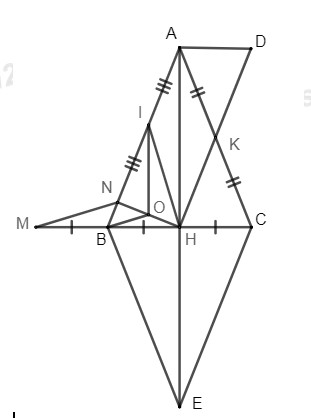
a)Xét có: lần lượt là trung điểm của và (gt)
là đường trung bình của (dấu hiệu nhận biết đường trung bình của tam giác)
(tính chất đường trung bình của tam giác)
tứ giác là hình thang (dhnb)
b)Xét tứ giác có: là trung điểm của và (gt) nên suy ra tứ giác là hình bình hành (dhnb)
Lại có, cân tại (tính chất tam giác cân)
Hình bình hành có hai cạnh bên bằng nhau nên là hình thoi (dhnb)
c)Vì cân tại (gt), mà là trung tuyến
cũng là đường cao của
Mà
Lại có: (do thẳng hàng)
Tứ giác là hình bình hành (dhnb)
(tính chất)
d)Gọi là trung điểm của và là trung điểm của là đường trung bình của (dhnb)
(tính chất)
Mà hay là đường cao của tam giác
Xét có đường cao HN và IO cắt nhau tại O nên O là trực tâm của
là đường cao của
Hay
Xét có: là trung điểm của là trung điểm của
là đường trung bình của (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra .
Bài 5:
Ta có:
Dấu “=” xảy ra
Thay vào ta có:
Đề thi Học kì 1 Toán lớp 8 năm học 2022 - 2023 có đáp án (20 Đề) - Đề 17
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Môn: Toán 8
Thời gian làm bài: 90 phút
(Đề 17)
Bài 1 (1 điểm) Chọn đáp án đúng nhất.
1. Thu gọn biểu thức: được kết quả là:
A.
B.
C.
D.
2. Giá trị của phân thức: không xác định tại các giá trị của biến là:
A.
B.
C.
D.
3. Tam giác vuông cân có độ dài đường trung tuyến ứng với cạnh huyền bằng thì độ dài cạnh góc vuông của tam giác đó bằng:….
4. Xét 4 khẳng định sau:
a) Biểu thức là bình phương của một tổng khi .
b) Dư trong phép chia đa thức cho đa thức là.
c) Hình thang có hai góc bằng nhau là hình thang cân.
d) Hai đỉnh và của hình thoi đối xứng với nhau qua đường thẳng .
Trong 4 khẳng định trên, có bao nhiêu khẳng định đúng?
A. Một
B. Hai
C. Ba
D. Bốn
Bài 2 (3 điểm)
1. Phân tích đa thức thành nhân tử:
a)
b)
2. Tìm biết:
3. Chứng minh giá trị biểu thức là số nguyên tố với mọi giá trị của .
Bài 3 (2,5 điểm)
Bài 4 (1,5 điểm)Cho vuông tại , có là trung điểm của . Gọi lần lượt là hình chiếu của trên và .
Bài 5 (1 điểm)
Đáp án đề kiểm tra Học kì Toán 8
Bài 1.
1. Chọn D
2. Chọn C
3.
Cho vuông cân tại , có là đường trung tuyến, .
Vì vuông cân tại , có là đường trung tuyến (gt)
(trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy)
Áp dụng định lý Py-ta-go có:
4. Chọn B.
Bài 2:
1. Ta có:
2. Ta có:
Vậy
Bài 3:
1. Phân thức xác định khi và chỉ khi
Thay vào biểu thức ta được:
2.
Biến đổi vế trái của đẳng thức ta có:
3. Ta có:
Vì là số nguyên tố nên là số nguyên tố với mọi
Bài 4:
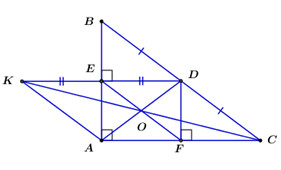
1. Xét tứ giác có: là hình chữ nhật (dhnb)
(tính chất hình chữ nhật)
2. Gọi là giao điểm của và là trung điểm của và (tính chất hình chữ nhật) (1)
(tính chất trung điểm)
Do D và K đối xứng nhau qua E nên suy ra (tính chất đối xứng)
Mà (từ vuông góc đến song song)
Ta có: là đường trung bình của (E, D là trung điểm của AB, BC (gt))
Xét tứ giác ta có:
là hình bình hành (dhnb)
cắt nhau tại trung điểm của mỗi đường (tính chất)
Mà O là trung điểm của EF (cách gọi)
đồng quy tại (đpcm)
Bài 5:
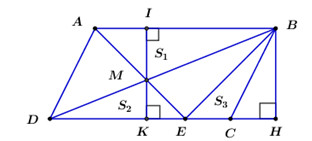
1. Kẻ như hình vẽ. Ta có:
2. Ta có:
- TH1: Nếu
- TH2: Nếu
Khi
Do đó (1)
Ta có: (2)
Cộng vế với vế của (1) và (2) ta được:
Dấu “=” xảy ra khi và chỉ khi
Vậy .
Đề thi Học kì 1 Toán lớp 8 năm học 2022 - 2023 có đáp án (20 Đề) - Đề 18
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Môn: Toán 8
Thời gian làm bài: 90 phút
(Đề 18)
Bài 1: (2 điểm)Chọn chữ cái trước đáp án đúng:
1. Đa thức bằng:
A.
B.
C.
D.
2. Kết quả của phép cộng: là:
A.
B.
C.
D.
3. Kết quả rút gọn biểu thức: là:
A.
B.
C.
D.
4. Số dư khi chia đa thức: cho đa thức là:
A.
B.
C.
D.
5. Hình vuông có độ dài đường chéo là . Độ dài cạnh hình vuông đó là:
A.
B.
C.
D.
6. Một hình chữ nhật có diện tích . Nếu tăng chiều dài lên hai lần, chiều rộng lên ba lần thì diện tích của hình chữ nhật mới là:
A.
B.
C.
D.
7. Cho hình thang cân có thì bằng:
A.
B.
C.
D. Không tính được.
8. Tứ giác có các đỉnh là trung điểm các cạnh của một tứ giác có hai đường chéo bằng nhau là:
A. Hình thang cân
B. Hình chữ nhật
C. Hình thoi
D. Hình vuông
Bài 2: (1,0 điểm)Phân tích đa thức sau thành nhân tử:
a)
b)
Bài 3: (1,5 điểm)
a) Chứng minh rằng giá trị biểu thức sau không phụ thuộc vào giá trị của biểu thức:
b) Tìm biết:
Bài 4: Thực hiện phép tính:
a)
b)
Bài 5: Cho có là phân giác của . Từ kẻ các đường thẳng song song với và , chúng cắt tại và .
a) Chứng minh: Tứ giác là hình thoi.
b) Trên tia lấy điểm sao cho là trung điểm . Chứng minh: Tứ giác là hình bình hành.
c) Gọi là điểm đối xứng của qua , tia cắt tia tại . Gọi là giao điểm của và . Chứng minh: đối xứng với qua .
d) Tìm điều kiện của để tứ giác là hình vuông.
Bài 6: Tính giá trị của biểu thức:
Đáp án đề kiểm tra Học kì Toán 8
Bài 1:
|
1D |
2C |
3A |
4B |
|
5A |
6C |
7B |
8C |
Bài 2:
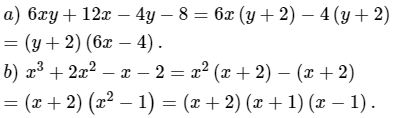
Bài 3:

Bài 4:
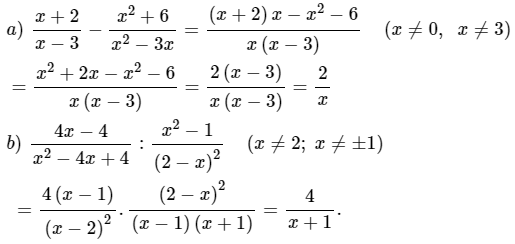
Bài 5:
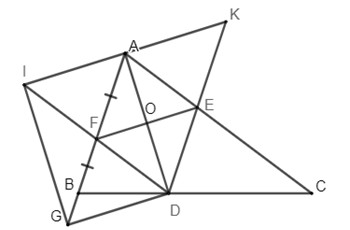
a) Xét tứ giác có: là hình bình hành (dhnb)
Lại có, là phân giác của hình bình hành là hình thoi (dhnb)
b) Vì là hình thoi (cmt)
(tính chất hình thoi)
Mà là trung điểm của (tính chất trung điểm)
Mà là hình hình hành (dhnb)
c) Vì là điểm đối xứng của qua (gt) là trung điểm của (tính chất hai điểm đối xứng qua một điểm)
Xét tứ giác có và cắt nhau tại trung điểm của mỗi đường (cmt)
là hình bình hành (dhnb)
(tính chất)
(do thẳng hàng) (1)
Lại có, (2)
Từ (1) và (2) là hình bình hành (dhnb)
Mà hai đường chéo cắt nhau tại trung điểm O nên suy ra đối xứng với qua . (đpcm)
d) Hình thoi là hình vuông khi và chỉ vuông tại .
Thật vậy, ta có: là hình vuông nên suy ra
mà AD là phân giác của vuông tại A.
Bài 6:
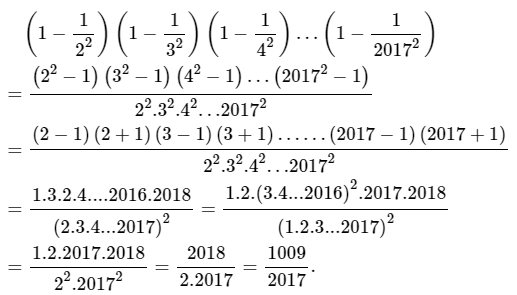
Đề thi Học kì 1 Toán lớp 8 năm học 2022 - 2023 có đáp án (20 Đề) - Đề 19
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Môn: Toán 8
Thời gian làm bài: 90 phút
(Đề 19)
Bài 1 (2 điểm) Phân tích các đa thức sau thành nhân tử:
a)
b)
Bài 2 (1 điểm) Thực hiện phép tính:
a)
b)
Bài 3 (2,5 điểm) Tìm số thực, biết:
a)
b)
Bài 4 (2,5 điểm) Cho biểu thức
a) Tìm điều kiện của để biểu thức xác định.
b) Rút gọn biểu thức A.
c) Tính giá trị của biểu thức A khi .
Bài 5 (4 điểm) Cho vuông tại , đường cao . Biết . Gọi lần lượt là chân các đường vuông góc hạ từ xuống và .
a) Tính diện tích .
b) Chứng minh tứ giác là hình chữ nhật.
c) Tính độ dài đoạn .
d) Gọi là trung điển của . Tính .
Bài 6 (0,5 điểm) Cho . Tính giá trị của biểu thức:
Đáp án đề kiểm tra Học kì Toán 8
Bài 1:
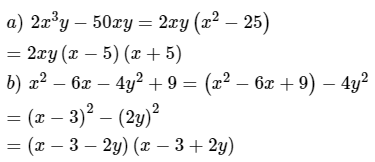
Bài 2:
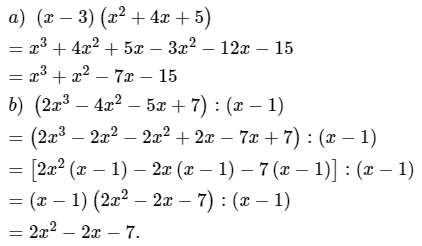
Bài 3:

Bài 4:
Điều kiện xác định:
c) Ta có:
Thay vào ta có:
Thay vào ta có:
Bài 5:
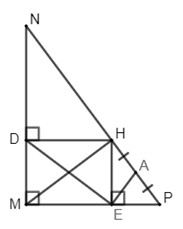
a) Xét , áp dụng định lý Py-ta-go ta có:
Diện tích có:
b) Ta có:
Xét tứ giác có: là hình chữ nhật (dhnb)
c) Ta có:
Lại có là hình chữ nhật (cmt) (hai đường chéo hình chữ nhật).
d)Vì là hình chữ nhật (cmt)
(tính chất hình chữ nhật)
Xét có là trung điểm của là đường trung tuyến của tam giác
(tính chất trong tam giác vuông có đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy)
là tam giác cân tại A (dấu hiệu nhận biết tam giác cân)
(tính chất tam giác cân)
Mà
Bài 6:
Vì nên ta có:
Đề thi Học kì 1 Toán lớp 8 năm học 2022 - 2023 có đáp án (20 Đề) - Đề 20
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Môn: Toán 8
Thời gian làm bài: 90 phút
(Đề 20)
I. TRẮC NGHIỆM (2 điểm)
Câu 1 : Phân thức: xác định với:
A. B.
C. D.
Câu 2 : Biểu thức P trong đẳng thức: là:
A. B.
C. D.
Câu 3 : Hình vuông có đường chéo bằng thì cạnh bằng:
A. B.
C. D.
Câu 4 : Hình thoi có hai đường chéo bằng và thì cạnh bằng:
A. B.
C. D.
II. TỰ LUẬN (8 điểm)
Bài 1: Phân tích đa thức thành nhân tử:
a)
b)
Bài 2: Thực hiện phép tính:
a)
b)
Bài 3: (2,0 điểm) Cho biểu thức:
a)Tìm giá trị của để giá trị của biểu thức A xác định.
b)Rút gọn A.
Bài 4: Cho hình vuông . Trên các cạnh lần lượt lấy các điểm sao cho .
a) Chứng minh tứ giác là hình bình hành.
b) Chứng minh tứ giác là hình chữ nhật.
c) Gọi là hình chiếu của trên . Tính .
Bài 5: Cho chứng minh:
Đáp án đề kiểm tra Học kì Toán 8
I. Trắc nghiệm
|
Câu 1 |
Câu 2 |
Câu 3 |
Câu 4 |
|
D |
B |
C |
A |
II. Tự luận
Bài 1:
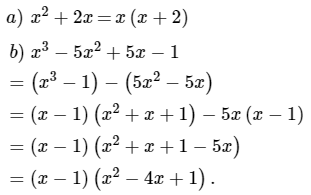
Bài 2:
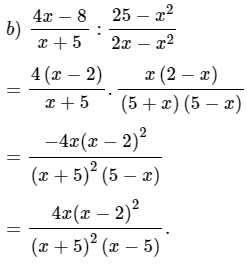
Bài 3:
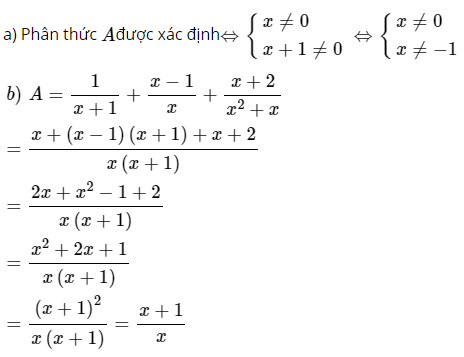
Bài 4:
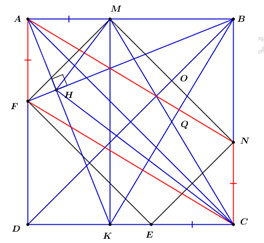
a)Vì là hình vuông (gt)
(tính chất hình vuông)
mà là hình bình hành (dhnb)
b)Vì là hình vuông (gt)
(tính chất hình vuông)
Mà (định lý Ta-let )(1)
Xét và có:
(2 cạnh góc vuông)
(2 cạnh tương ứng) (2)
Từ (1) và (2) là hình bình hành (dhnb)
Vì là hình vuông (gt) là phân giác của (tính chất hình vuông)
(tính chất tia phân giác) hay
Ta có:
Gọi
Xét và có:
(2 góc tương ứng)
Mà
Mà
Do đó hình bình hành là hình chữ nhật (dhnb)
c) Gọi cắt tại .
Xét có: (2 góc nhọn phụ nhau)
Xét có: (2 góc nhọn phụ nhau)
Xét và có:
(cạnh góc vuông – góc nhọn)
(2 cạnh tương ứng)
Mà
Lại có: (3)
Mà (4)
Từ (3) và (4) suy ra là hình bình hành (dhnb)
Lại có, hình bình hành là hình chữ nhật (dhnb)
(tính chất)
Gọi là giao điểm của và là trung điểm của mỗi đường.
Xét có: (trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy)
vuông tại (trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy)
Bài 5:
Vì nên ta có:
Bất đẳng thức luôn đúng với mọi thỏa mãn