Bộ 10 Đề thi Toán lớp 8 Học kì 2 có đáp án năm 2023

Quý Lê Xuân Ngày: 08-03-2024 Lớp 8

Mua tài liệu 24 8.3 K 51

Tài liệu Bộ đề thi Toán lớp 8 học kì 2 có đáp án năm học 2022 - 2023 gồm 4 đề thi tổng hợp từ đề thi môn Toán 8 của các trường THCS trên cả nước đã được biên soạn đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi học kì 2 Toán lớp 8. Mời các bạn cùng đón xem:

Chỉ 100k mua trọn bộ Đề thi học kì 2 Toán 8 bản word có lời giải chi tiết (chỉ 20k cho 1 đề thi bất kì):

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi Toán lớp 8 Học kì 2 có đáp án năm 2023 - Đề 1

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 1)

Phần trắc nghiệm (2 điểm)

Câu 1: x = 4 là nghiệm của phương trình

A/ 3x - 1 = x - 5 B/ 2x - 1 = x + 3

C/ x - 3 = x - 2 D/ 3x + 5 =-x - 2

Câu 2: Cho hai phương trình : x(x - 1) (I) và 3x - 3 = 0(II)

A/ (I)tương đương (II)

B/ (I) là hệ quả của phương trình (II)

C/ (II) là hệ quả của phương trình (I)

D/ Cả ba đều sai

Câu 3: Cho biết 2x - 4 = 0.Tính 3x - 4 bằng:

A/ 0 B/ 2 C/ 17 D/ 11

Câu 4: Phương trình có nghiệm là :

A/{-1} B/ {-1; 3} C/ {-1; 4} D/ S = R

Câu 5: Bất phương trình :x² + 2x + 3 > 0 có tập nghiệm là :

A/ Mọi x ∈ R B/ x ∈ φ C/ x > -2 D/ x ≥ -2

Câu 6: Để biểu thức (3x + 4) - x không âm giá trị của x phải là :

A/ x ≥ -2 B/ -x ≥ 2 C/ x ≥ 4 D/ x ≤ -4

Câu 7: Cho hình vẽ : NQ//PK ; Biết MN = 1cm ;MQ = 3cm ; MK = 12cm. Độ dài NP là:

Bộ Đề thi Toán lớp 8

A/ 0,5 cm B/ 2cm C/ 4cm D/ 3cm

Câu 8: ΔABC đồng dạng với Δ DEF theo tỉ số đồng dạng k₁ ;ΔDEF đồng dạng với ΔGHK theo tỉ số đồng dạng k₂ . ΔABC đồng dạng với Δ GHK theo tỉ số :

A/ k₁/k₂ B/ k₁ + k₂ C/ k₁ - k₂ D/ k₁ .k₂

Phần tự luận (8 điểm)

Bài 1: (2 điểm) Giải phương trình và bất phương trình sau:

a) |3x| = x + 6

c) (x + 1)(2x – 2) – 3 > –5x – (2x + 1)(3 – x)

Bài 2: (2 điểm) Một tổ sản xuất theo kế hoạch mỗi ngày phải sản xuất 50 sản phẩm. Khi thực hiện mỗi ngày tổ sản xuất 57 sản phẩm. Do đó, tổ đã hoàn thành trước kế hoạch 1 ngày và còn vượt mức 13 sản phẩm. Hỏi theo kế hoạch, tổ phải sản xuất bao nhiêu sản phẩm?

Bài 3: (0,5 điểm) Chứng minh rằng nếu a > 0, b > 0, c > 0 và a < b thì

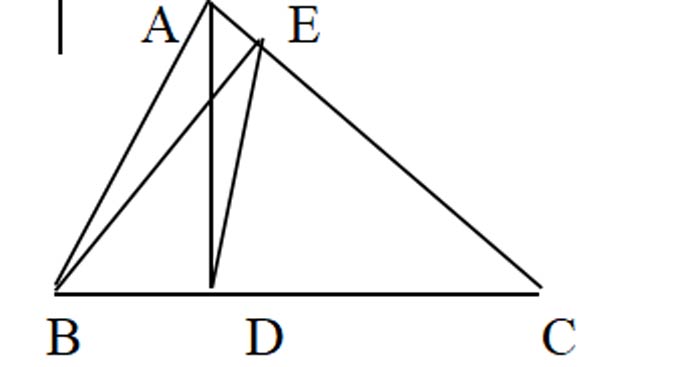
Bài 4: (3,5 điểm) Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H.

a) Chứng minh ΔAEB và ΔAFC đồng dạng. Từ đó suy ra: AF.AB = AE.AC

b) Chứng minh ∠AEF = ∠ABC

c) Cho AE = 3cm, AB = 6cm. Chứng minh rằng SABC = 4SAEF

d) Chứng minh Bộ Đề thi Toán lớp 8

Đáp án và Hướng dẫn giải

Phần trắc nghiệm (2 điểm)

1.B	3.B	5.A	7.D
2.C	4.A	6.A	8.D

Phần tự luận (8 điểm)

Bài 1

a) |3x| = x + 6 (1)

Ta có 3x = 3x khi x ≥ 0 và 3x = -3x khi x < 0

Vậy để giải phương trình (1) ta quy về giải hai phương trình sau:

+ ) Phương trình 3x = x + 6 với điều kiện x ≥ 0

Ta có: 3x = x + 6 ⇔ 2x = 6 ⇔ x = 3 (TMĐK)

Do đó x = 3 là nghiệm của phương trình (1).

+ ) Phương trình -3x = x + 6 với điều kiện x < 0

Ta có -3x = x + 6 ⇔ -4x + 6 ⇔ x = -3/2 (TMĐK)

Do đó x = -3/2 là nghiệm của phương trình (1).

Vậy tập nghiệm của phương trình đã cho S = {3; -3/2}

ĐKXĐ: x ≠ 0, x ≠ 2

Quy đồng mẫu hai vễ của phương trình, ta được:

Bộ Đề thi Toán lớp 8

Vậy tập nghiệm của phương trình là S = {-1}

c) (x + 1)(2x – 2) – 3 > –5x – (2x + 1)(3 – x)

⇔ 2x² – 2x + 2x – 2 – 3 > –5x – (6x – 2x² + 3 – x)

⇔ 2x² – 5 ≥ –5x – 6x + 2x² – 3 + x

⇔ 10x ≥ 2 ⇔ x ≥ 1/5

Tập nghiệm: S = {x | x ≥ 1/5}

Bài 2

Gọi số sản phẩm theo kế hoạc tổ sản xuất là x (sản phẩm)

Điều kiện: x nguyên dương, x > 57

Thời gian dự dịnh theo kế hoạch là: x/50 (ngày)

Số sản phẩm về sau là: x + 13 (sản phẩm)

Thời gian thực tế tổ sản xuất là:

Theo đề ta có phương trình:

⇔ 57x - 50(x + 13) = 2850

⇔ 57x - 50x - 650 = 2850

⇔ 7x = 3500 ⇔ x = 500 (TMĐK)

Vậy theo kế hoạch tổ sản xuất là 500 sản phẩm.

Bài 3

Ta có:

⇔ a(b + c) < (a + c)b

(vì a > 0, b > 0 và c > 0 ⇔ b + c > 0 và a + c > 0)

⇔ ab + ac < ab + bc

⇔ ac < bc ⇔ a < b (luôn đúng, theo gt)

Bài 4

Bộ Đề thi Toán lớp 8

a) Xét ΔAEB và ΔAFC có:

∠AEB = ∠AFC = 90^o (gt)

∠A chung

Vậy ΔAEB ∼ ΔAFC (g.g)

b) Xét ΔAEF và ΔABC có

∠A chung

AF.AB = AE.AC (Cmt)

⇒ ΔAEF ∼ ΔABC (c.g.c)

⇒ ∠AEF = ∠ABC

c) ΔAEF ∼ ΔABC (cmt)

Bộ Đề thi Toán lớp 8

......................................................................

Đề thi Toán lớp 8 Học kì 2 có đáp án năm 2023 - Đề 2

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 2)

Bài 1: (3 điểm) Giải phương trình và bất phương trình:

Bộ Đề thi Toán lớp 8

C) x – 2)² + 2(x – 1) ≤ x² + 4

Bài 2: (2 điểm) Một ô tô đi từ A đến B với vận tốc 60km/h và đi từ B về A với vận tốc 45km/h. Thời gian cả đi và về hết 7 giờ. Tính quãng đường AB.

Bài 3: (1 điểm)Chứng minh rằng nếu a + b = 1 thì a² + b2 ≥ 1/2

Bài 4: (4 điểm) Cho hình thang ABCD (AB // CD) có AB = AD = CD/2. Gọi M là trung điểm của CD và H là giao điểm của AM và BD.

a) Chứng minh tứ giác ABMD là hình thoi

b) Chứng minh BD ⊥ BC

c) Chứng minh ΔAHD và ΔCBD đồng dạng

d) Biết AB = 2,5cm; BD = 4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD.

Đáp án và Hướng dẫn giải

Bài 1

a) Điều kiện: x + 2 ≠ 0 và x – 2 ≠ 0 ⇔ x ≠ ± 2

(Khi đó: x² – 4 = (x + 2)(x – 2) ≠ 0)

Bộ Đề thi Toán lớp 8

Vậy tập nghiệm của pt là: S = {-1; 1}

b) Điều kiện: 2x ≥ 0 ⇔ x ≥ 0

Khi đó: |x – 5| = 2x ⇔ x – 5 = 2x hoặc x – 5 = -2x

⇔ x = -5 hoặc x = 5/3

Vì x ≥ 0 nên ta lấy x = 5/3 . Tập nghiệm : S = {5/3}

c) x – 2)² + 2(x – 1) ≤ x² + 4

⇔ x² – 4x + 4 + 2x – 2 ≤ x² + 4

⇔ -2x ≤ 2

⇔ x ≥ -1

Tập nghiệm S = {x | x ≥ -1}

Bài 2

Gọi x (km) là quãng đường AB (x > 0)

Thời gian đi từ A đến B là: x/60 (giờ)

Thời gian đi từ B về A là: x/45 (giờ)

Theo đề ra, ta có phương trình:

⇔ 3x + 4x = 7.180 ⇔ 7x = 7.180 ⇔ x = 180 (nhận)

Trả lời: Quãng đường AB dài 180km.

Bài 3

Ta có: a + b = 1 ⇔ b = 1 – a

Thay vào bất đẳng thức a² + b² ≥ 1/2 , ta được:

a² + (1 – a)² ≥ 1/2 ⇔ a² + 1 – 2a + a² ≥ 1/2

⇔ 2a² – 2a + 1 ≥ 1/2 ⇔ 4a² – 4a + 2 ≥ 1

⇔ 4a² – 4a + 1 ≥ 0 ⇔ (2a – 1)² ≥ 0 (luôn đúng)

Vậy bất đẳng thức được chứng minh

Bài 4

Bộ Đề thi Toán lớp 8

a) Ta có: AB = AD = CD/2 và M là trung điểm của CD (gt)

⇔ AB = DM và AB // DM

Do đó tứ giác ABMD là hình bình hành có AB = AD. Vậy ABMD là hình thoi.

b) M là trung điểm của CD nên BM là trung tuyến của ΔBDC mà MB = MD = MC. Do đó ΔBDC là tam giác vuông tại B hay DB ⊥ BC

c) ABMD là hình thoi (cmt) ⇔ ∠D1 = ∠D₂

Do đó hai tam giác vuông AHD và CBD đồng dạng (g.g)

d) Ta có :

Xét tam giác vuông AHB, ta có :

Bộ Đề thi Toán lớp 8

Dễ thấy tứ giác ABCM là hình bình hành (AB // CM và AB = CM)

⇒ BC = AM = 3 (cm)

Ta có:

M là trung điểm của DC nên

S_BMD = S_BMC = S_BCD/2 = 3 (cm²) (chung đường cao kẻ từ B và MD = MC)

Mặt khác ΔABD = ΔMDB (ABCD là hình thoi)

⇔ S_ABD = S_BMD = 3 (cm²)

Vậy S_ABCD = S_ABD + S_BMD + S_BMC = 9 (cm²)

......................................................................

Đề thi Toán lớp 8 Học kì 2 có đáp án năm 2023 - Đề 3

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 3)

Phần trắc nghiệm (2 điểm)

Câu 1: Trong các phương trình sau; phương trình nào là bậc nhất một ẩn?

A/ x – 5 = x + 3 B/ ax + b = 0

C/ (x - 2)( x + 4) = 0 D/ 2x + 1 = 4x + 3

Câu 2: Phương trình : x2 =-9 có nghiệm là :

A/ Một nghiệm x = 3 B/ Một nghiệm x = -3

C/ Có hai nghiệm : x = -3; x = 3 D/ Vô nghiệm

Câu 3: Giá trị của b để phương trình 3x + b =0 có nghiệm x = -3 là :

A/ 4 B/ 5 C/9 D/ KQ khác

Câu 4: Phương trình : có nghiệm là :

A/ 0 B/ 1 C/ 2 D/Kết quả khác

Câu 5: x ≥ 0 và x > 4 thì

A/ 0 ≤ x < 4 B/ x > 4 C/ x ≥ 4 D/ x ∈ ∅

Câu 6: Bất phương trình có nghiệm là :

A/ x < 1 B/ x < 2 C/ x > 2 D/ KQ khác

Câu 7: Cho các đoạn thẳng AB=8cm ;CD = 6cm ; MN = 12mm. PQ = x. Tìm x để AB và CD tỉ lệ với MN;PQ

A/ x = 9 cm B/ x = 0,9cm C/ x = 18 cm D/ Cả ba đều sai

Câu 8: Cho ΔABC đồng dạng với ΔA’B’C’. Biết và hiệu số chu vi của ΔA’B’C’và chu vi của ΔABC là 30. Phát biểu nào đúng

A/ C_ΔABC =20 ;C_{ΔA’B’C’}= 50 B/ C_{ΔABC =50} ;C_{ΔA’B’C’= 20}

C/ C_ΔABC = 45 ;C_{ΔA’B’C’}= 75 D/ Cả ba đều sai

Phần tự luận (8 điểm)

Bài 1: (2,5 điểm) Giải phương trình và bất phương trình sau :

Bộ Đề thi Toán lớp 8

Bài 2: (1,5 điểm) Hai người cùng làm chung một công việc hết 12 ngày. Năng suất trong một ngày của người thứ hai bằng 2/3 năng suất người thứ nhất. Hỏi nếu làm một mình thì mỗi người phải làm trong bao lâu mới xong công việc ?

Bài 3: (0,5 điểm) Cho a > 0 và b > 0. Chứng minh rằng:

Bộ Đề thi Toán lớp 8

Bài 4: (3,5 điểm) Cho tam giác ABC có ba góc nhọn, biết AB = 15cm, AC = 13cm và đường cao AH = 12cm. Gọi N, M lần lượt là hình chiếu vuông góc của H xuống AC và AB.

a) Chứng minh rằng ΔAHN ∼ ΔACH

b) Tính độ dài BC

c) Chứng minh ΔAMN ∼ ΔACB

d) Tính MN

Đáp án và Hướng dẫn giải

Phần trắc nghiệm (2 điểm)

1. D	2. D	3.C	4.A
5.B	6.C	7.B	8.A

Phần tự luận (8 điểm)

Bài 1

a) Điều kiện: x ≠ 0 và x ≠ 1

MTC: x(x – 1)

Bộ Đề thi Toán lớp 8

(thỏa mãn ĐKXD)

Tập nghiệm của (1): S = {3/5}

b) (2) ⇔ |1 – 2x| = 2x – 1 ⇔ |2x – 1| = 2x – 1

Ta biết |A| = A nếu A ≥ 0. Vậy 2x – 1 ≥ 0 ⇔ x ≥ 1/2

Tập nghiệm của (2) : S = {x | x ≥ 1/2}

Bộ Đề thi Toán lớp 8

⇔4(x + 1) – 12 ≥ 3(x – 2)

⇔ 4x + 4 – 12 ≥ 3x – 6

⇔ 4x – 3x ≥ 8 – 6

⇔ x ≥ 2

Tập nghiệm: S = {x | x ≥ 2}

Bài 2

Gọi x là số ngày để người thứ nhất làm một mình xong công việc (x ∈ N*)

Một ngày người thứ nhất làm được 1/x công việc

Một ngày người thứ hai làm được

Bộ Đề thi Toán lớp 8

Một ngày cả hai người làm được

Bộ Đề thi Toán lớp 8

Hai người làm chung thì xong công việc trong 12 ngày nên một ngày cả 2 người làm được 1/12 công việc

Do đó, ta có phương trình:

Bộ Đề thi Toán lớp 8

⇔ 12 + 8 = x ⇔ x = 20 (nhận)

Trả lời: Người thứ nhất làm trong 20 ngày; người thứ hai làm trong 30 ngày.

Bài 3

Bộ Đề thi Toán lớp 8

Vậy bất đẳng thức được chứng minh.

Bài 4

Bộ Đề thi Toán lớp 8

a) Xét ΔANH và ΔAHC có:

∠(NAH) chung

∠(ANH) = ∠(AHC) = 90^o

⇒ ΔANH ∼ ΔAHC (g.g)

b) Ta có :

Tương tự : CH = 5 (cm)

⇒ BC = BH + CH = 9 + 5 = 14 (cm)

c) Theo chứng minh trên ta có:

Bộ Đề thi Toán lớp 8

Chứng minh tương tự ta có :

ΔAMH ∼ ΔAHB ⇒ AH² = AM.AB (2)

Từ (1) và (2) ⇒ AN.AC = AM.AB nên 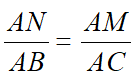Bộ Đề thi Toán lớp 8 (3)

Xét ΔAMN và ΔACB có :

∠A chung

Bộ Đề thi Toán lớp 8

⇒ ΔAMN ∼ ΔACB (c.g.c)

d) Ta có : ΔAMH ∼ ΔAHB

Lại có ΔAMN ∼ ΔACB (cmt)

......................................................................

Đề thi Toán lớp 8 Học kì 2 có đáp án năm 2023 - Đề 4

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 4)

Bài 1: ( 3đ ) Giải phương trình sau đây :

a) 8( 3x - 2 ) - 14x = 2( 4 – 7x ) + 15x

b) ( 3x – 1 )( x – 3 ) – 9 + x² = 0

c) |x-2| = 2x-3

Bài 2: ( 1đ ) : Giải bất phương trình sau đây và biểu diễn tập nghiệm trên trục số :

Bài 3: (1 điểm) Tìm giá trị lớn nhất của A = -x² + 2x + 9

Bài 4: ( 1,5đ ) : Giải bài toán bằng cách lập phương trình :

Một người đi xe máy dự định đi từ A đến B với vận tốc 36km/h. Nhưng khi thực hiện người ấy giảm vận tốc 6km/h nên đã đến B chậm hơn dự định là 24 phút. Tính quãng đường AB

Bài 5: ( 3,5đ ) :Cho tam giác ABC vuông tại A có AH là đường cao. Vẽ HD ⊥ AB ( D ∈ AB ). HE ⊥ AC ( E ∈ AC ). AB = 12cm, AC = 16 cm

a) Chứng minh : ΔHAC ∼ ΔABC

b) Chứng minh : AH² = AD.AB

c) Chứng minh : AD.AB = AE.AC.

d) Tính Bộ Đề thi Toán lớp 8

Đáp án và Hướng dẫn giải

Bài 1

a) 8( 3x - 2 ) - 14x = 2( 4 – 7x ) + 15x

⇔ 24x – 16 -14x = 8 – 14x + 15x

⇔ 10x -16 = 8 + x

⇔ 9x = 24

⇔ x = 24/9

b) ( 3x – 1 )( x – 3 ) – 9 + x² = 0

⇔ (3x -1)( x – 3) + (x - 3)( x + 3) = 0

⇔ (x - 3)(3x - 1 + x - 3) = 0

⇔ (x - 3)(4x - 4) = 0

Bộ Đề thi Toán lớp 8

c) |x - 2| = 2x - 3

TH1: x - 2 ≥ 0 ⇔ x ≥ 2

Khi đó: x - 2 = 2x – 3

⇔ 2x – x = -2 + 3

⇔ x = 1 (không TM điều kiện x ≥ 2)

TH2: x – 2 < 0 ⇔ x < 2

Khi đó: x-2 = -(2x – 3)

⇔ x – 2 = -2x + 3

⇔ 3x = 5

⇔ x = 5/3 ( TM điều kiện x < 2)

Bộ Đề thi Toán lớp 8

MTC: x(x-2)

ĐKXĐ: x ≠ 0;x ≠ 2

Bộ Đề thi Toán lớp 8

Đối chiếu với ĐKXĐ thì pt có nghiệm x = - 1

Bài 2

Bộ Đề thi Toán lớp 8

⇔ 2x - 2 - 9x - 15 ≥ 6 - 4x - 5

⇔ 2x - 9x + 4x ≥ 6 - 5 + 2 + 15

⇔ -3x ≥ 18

⇔ x ≤ -6

Vậy tập nghiệm của phương trình là S= {x|x ≤ -6}

Biểu diễn nghiệm trên trục số:

Bộ Đề thi Toán lớp 8

Bài 3: A = -x² + 2x + 9 = -(x² – 2x + 1) + 10 = - (x + 1)² + 10

Ta có: -(x - 1)² ≤ 0 ∀x

-(x - 1)² + 10 ≤ 10

Dấu bằng xảy ra khi (x - 1)² = 0 ⇔ x = 1

Vậy GTLN của A là 10, đạt được khi x = 1

Bài 4

Gọi quãng đường AB là x (km) (x > 0)

Thời gian người đó dự định đi là: x/36 (km)

Vận tốc đi thực tế là: 36 – 6 = 30 (km)

Thời gian thực tế người đó đi là: x/30 (km)

Do đến B chậm hơn dự tính 24’ = 2/5 h nên ta có phương trình:

Bộ Đề thi Toán lớp 8

⇔ 5x + 36 = 6x

⇔ x = 36

Vậy quãng đường AB là 36 km.

Bài 5

Bộ Đề thi Toán lớp 8

a) Xét ΔHAC và ΔABC có:

∠(ACH ) là góc chung

∠(BAC)= ∠(AHC) = 90^o

⇒ ΔHAC ∼ ΔABC (g.g)

b) Xét ΔHAD và ΔBAH có:

∠(DAH ) là góc chung

∠(ADH) = ∠(AHB) = 90^o

⇒ ΔHAD ∼ ΔBAH (g.g)

c) Tứ giác ADHE có 3 góc vuông ⇒ ADHE là hình chữ nhật.

⇒ ΔADH= ΔAEH ( c.c.c) ⇒ ∠(DHA)= ∠(DEA)

Mặt khác: ΔHAD ∼ ΔBAH ⇒ ∠(DHA)= ∠(BAH)

∠(DEA)= ∠(BAH)

Xét ΔEAD và ΔBAC có:

∠(DEA)= ∠(BAH)

∠(DAE ) là góc chung

ΔEAD ∼ ΔBAC (g.g)

Bộ Đề thi Toán lớp 8

d) ΔEAD ∼ ΔBAC

Bộ Đề thi Toán lớp 8

ΔABC vuông tại A, theo định lí Pytago:

Bộ Đề thi Toán lớp 8

Theo b, ta có:

Bộ Đề thi Toán lớp 8

Đề thi Toán lớp 8 Học kì 2 có đáp án năm 2023 - Đề 5

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 5)

Bài 1: Cho hai biểu thức:

$A = \frac{{x + 2}}{{x + 5}} + \frac{{ - 5x - 1}}{{{x^2} + 6x + 5}} - \frac{1}{{1 + x}}$ và $B = \frac{{ - 10}}{{x - 4}}$ với $x \ne - 5,x \ne - 1,x \ne 4$

a, Tính giá trị của biểu thức B tại x = 2

b, Rút gọn biểu thức A

c, Tìm giá trị nguyên của x để P = A.B đạt giá trị nguyên

Bài 2: Giải các phương trình và bất phương trình sau:

Bài 3: Giải bài toán bằng cách lập phương trình

Một vòi nước chảy vào bể không có nước. Cùng lúc đó một vòi nước khác chảy từ bể ra. Mỗi giờ lượng nước vòi chảy ra bằng 4/5 lượng nước chảy vào. Sau 5 giờ thì bên trong bể đạt tới 1/8 dung tích bể. Hỏi nếu bể không có nước mà chỉ mở vòi chảy vào thì sau bao lâu thì đầy bể?

Bài 4: Cho tam giác ABC vuông tại A có AH là đường cao (H thuộc BC). Gọi D và E lần lượt là hình chiếu của H trên AB và AC. Chứng minh rằng:

a, AEHD là hình chữ nhật

b, $\Delta ABH \sim \Delta AHD$

c, $H{E^2} = AE.EC$

d, Gọi M là giao điểm của BE và CD. Chứng minh rằng $\Delta DBM\sim\Delta ECM$

Bài 5: Giải phương trình: $\left| {x - 2017} \right| + \left| {2x - 2018} \right| + \left| {3x - 2019} \right| = x - 2020$

Đáp án đề thi học kì 2 môn Toán lớp 8

Bài 1:

a, Thay x = 2 (thỏa mãn điều kiện) vào B ta có: $B = \frac{{ - 10}}{{2 - 4}} = \frac{{ - 10}}{{ - 2}} = 5$

b, $A = \frac{{x + 2}}{{x + 5}} + \frac{{ - 5x - 1}}{{{x^2} + 6x + 5}} - \frac{1}{{1 + x}}$ (điều kiện: $x \ne - 5,x \ne - 1$ )

$= \frac{{x + 2}}{{x + 5}} + \frac{{ - 5x - 1}}{{\left( {x + 1} \right)\left( {x + 5} \right)}} - \frac{1}{{1 + x}}$

$= \frac{{\left( {x + 2} \right)\left( {x + 1} \right)}}{{x + 5}} + \frac{{ - 5x - 1}}{{\left( {x + 1} \right)\left( {x + 5} \right)}} - \frac{{x + 5}}{{1 + x}}$

$= \frac{{{x^2} + 3x + 2 - 5x - 1 - x - 5}}{{\left( {x + 1} \right)\left( {x + 5} \right)}}$

$= \frac{{{x^2} - 3x - 4}}{{\left( {x + 1} \right)\left( {x + 5} \right)}} = \frac{{\left( {x + 1} \right)\left( {x - 4} \right)}}{{\left( {x + 1} \right)\left( {x + 5} \right)}} = \frac{{x - 4}}{{x + 5}}$

$P = A:B = \frac{{x - 4}}{{x + 5}}.\frac{{ - 10}}{{x - 4}} = \frac{{ - 10}}{{x + 5}}$

Để P nhận giá trị nguyên thì $\frac{{ - 10}}{{x + 5}}$ nhận giá trị nguyên hay

$x + 5 \in U\left( {10} \right) = \left\{ { \pm 1; \pm 2; \pm 5; \pm 10} \right\}$

Ta có bảng:

x + 5	-10	-5	-2	-1	1	2	5	10
x	-15 (tm)	-10 (tm)	-7 (tm)	-6 (tm)	-4 (tm)	-3 (tm)	0 (tm)	5 (tm)

Vậy với $x \in \left\{ { - 15; - 10; - 7; - 6; - 4; - 3;0;5} \right\}$ thì P = A.B nhận giá trị nguyên

Bài 2:

a, $x \in \left\{ { - 7;2} \right\}$ b, $x \le \frac{{ - 1}}{{13}}$

Bài 3:

Gọi thời gian vòi chảy vào đầy bể là x (giờ, x > 0)

Trong 1 giờ, vòi đó chảy được số phần bể là: $\frac{1}{x}$ bể

Trong 1 giờ, vòi chảy ra chiếm số phần bể là: $\frac{1}{x}.\frac{4}{5} = \frac{4}{{5x}}$ bể

Sau 6 giờ thì bên trong bể đạt tới 1/8 dung tích bể. Ta có phương trình:

$5.\left( {\frac{1}{x} - \frac{4}{{5x}}} \right) = \frac{1}{8}$

Giải phương trình tính ra được x = 8

Vậy thời gian vòi chảy đầy bể là 8 giờ

Bài 4:

a, Có HD vuông góc với AB $\Rightarrow \widehat {ADH} = {90^0}$ , HE vuông góc AC $\Rightarrow \widehat {AEH} = {90^0}$

Tứ giác ADHE có 3 góc vuông nên tứ giác ADHE là hình chữ nhật

b, Hai tam giác vuông ADH và AHB có góc $\widehat {BAH}$ chung nên hai tam giác đồng dạng với nhau theo trường hợp góc góc

c, Chứng minh $\widehat {ACH} = \widehat {AHE}$ (cùng phụ với góc $\widehat {EAH}$ ) để suy ra hai tam giác AEH và HEC đồng dạng rồi suy ra tỉ số $\frac{{AE}}{{HE}} = \frac{{EH}}{{EC}}$

d, $\Delta ABH\sim\Delta AHD \Rightarrow \frac{{AB}}{{AH}} = \frac{{AH}}{{AD}} \Rightarrow A{H^2} = AB.AD$

$\Delta ACH\sim\Delta AHE \Rightarrow \frac{{AC}}{{AH}} = \frac{{AH}}{{AE}} \Rightarrow A{H^2} = AC.AE$

Do đó AB.AD = AC. AE

Suy ra hai tam giác ABE và tam giác ACD đồng dạng

$\Rightarrow \widehat {ABE} = \widehat {ACD} \Rightarrow \Delta DBM\sim\Delta ECM$

Bài 5:

Nhận thấy vế bên trái luôn dương nên $x - 2020 \ge 0 \Leftrightarrow x \ge 2020$

Với $x \ge 2020 \Rightarrow \left\{ \begin{array}{l} x - 2017 \ge 0\\ 2x - 2018 \ge 0\\ 3x - 2019 \ge 0 \end{array} \right.$

Phương trình trở thành: x – 2017 + 2x – 2018 + 3x – 2019 = x – 2020

Hay kết hợp với điều kiện $x = \frac{{4034}}{5}$ suy ra phương trình đã cho vô nghiệm

Đề thi Toán lớp 8 Học kì 2 có đáp án năm 2023 - Đề 6

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 6)

Câu 1 ( 2đ) : .Một giáo viên theo dõi thời gian làm một bài toán ( tính theo phút) của 30 học sinh lớp 7 (ai cũng làm được) và ghi lại bảng sau:

9 7 9 10 9 8 10 5 14 8 10 8 8 8 9 9 10 7 5 14 5 5 8 8 9 7 8 9 14 8

a/ Dấu hiệu ở đây là gì?

b/ Lập bảng “ tần số”

c/ Tính số trung bình cộng .

d/ Tìm mốt của dấu hiệu.

Câu 2 ( 1 điểm) :

a/ Tìm bậc của đơn thức -2x²y³

b/ Tìm các đơn thức đồng dạng trong các đơn thức sau:

5xy³ ; 5x²y³ ; -4x³y² ; 11 x²y³

Câu 3 (1,5điểm): Cho hai đa thức

P(x) = 4x³ + x²- x + 5.

Q(x) = 2 x²+ 4x - 1.

a/ Tính :P(x) + Q(x)

b/ Tính: P(x) - Q(x)

Câu 4 ( 1,5 điểm) : Cho đa thức A(x) = x² – 2x .

a/ Tính giá trị của A(x) tại x = 2.

b/ Tìm các nghiệm của đa thức A(x).

Câu 5 ( 2 điểm)

a/Trong các tam giác sau ,tam giác nào là tam giác vuông cân,tam giác đều .

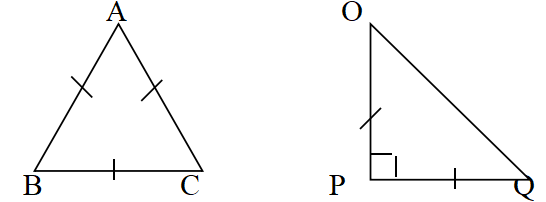
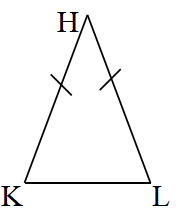
b/ Cho tam giác ABC có AB = 1 cm, AC = 6cm, . Tìm độ dài cạnh BC ,biết độ dài này là một số nguyên.

Câu 6 (2 đ) : Cho tam giác ABC vuông tại A, có AB = 3cm; AC = 4cm.

a/ Tính độ dài BC.

b/ Hai đường trung tuyến AM và BN cắt nhau tại G. Tính độ dài AG.

Đáp án đề kiểm tra học kì 2 môn Toán

Câu

Nội Dung

Thang điểm

Câu1

( 2đ)

a) Dấu hiệu: thời gian giải một bài toán.

0,5

b) Bảng “ tần số”

Thời gian(x)		7	8	9	10	14
Tần số(n)	4	3	9	7	4	3	N=30

0,5

c) Số trung bình cộng

X = ( 5.4+7.3+8.9+9.7+10.4+14.3) : 30 = 8,6

0.5

d) Mốt = 8

0,5

Câu 2

(1đ)

a) Bậc của đơn thức -2x²y³ là 5.

b) Các đơn thức đồng dạng là 5x²y³ và 11x²y³.

0,5

Câu 3

(1,5đ)

a) P(x) + Q(x) = 4x³ +3x² + 3x + 4

0,75

b) P(x) – Q(x) = 4x³ – x² -5x + 6

0,75

Câu 4 1,5đ)

a) A(2) = 2² – 2.2 = 0

0,5

Đề thi Toán lớp 8 Học kì 2 có đáp án năm 2023 - Đề 7

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 7)

Câu 1: (3 điểm) Giải các phương trình sau :

a) 2x - 3 = 5

b) (x + 2)(3x - 15) = 0

c) $\frac{3}{x+1}-\frac{2}{x-2}=\frac{4 x-2}{(x+1) \cdot(x-2)}$

Câu 2: (2 điểm)

a) Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số

$\frac{2 x+2}{3}<2+\frac{x-2}{2}$

b) Tìm x để giá trị của biểu thức 3x – 4 nhỏ hơn giá trị của biểu thức 5x – 6

Câu 3: (1,5 điểm) Một người đi xe máy từ Viên Thành đến Vinh với vận tốc 40 km/h. Lúc về người đó uống rượu nên đi nhanh hơn với vận tốc 70 km/h và thời gian về cũng ít hơn thời gian đi 45 phút. Tính quãng đường Viên Thành tới Vinh.

Câu 4:(3,5 điểm) Cho ABC vuông tại A, có AB = 12 cm ; AC = 16 cm. Kẻ đường cao AH, H∈BC).

a) Chứng minh: HBA ഗABC

b) Tính độ dài các đoạn thẳng BC, AH.

c) Trong ABC kẻ phân giác AD (D∈ BC). Trong ADB kẻ phân giác DE (E∈ AB); trong ADC kẻ phân giác DF (F∈ AC).

Chứng minh rằng: $\frac{E A}{E B}\cdot\frac{D B}{D C}\cdot\frac{F C}{F A}=1$

Đáp án đề thi học kì 2 lớp 8 môn Toán

Câu

Đáp án

Điểm

(3 đ)

a) 2x - 3 = 5

2x = 5 + 3

2x = 8

x = 4

Vậy tập nghiệm của phương trình là S = { 4}

b) $\begin{array}{l} \text { b) }(x+2)(3 x-15)=0 \\ \Leftrightarrow\left[\begin{array} { l } { x + 2 = 0 } \\ { 3 x - 1 5 = 0 } \end{array} \Leftrightarrow \left[\begin{array}{l} x=-2 \\ x=5 \end{array}\right.\right. \end{array}$

Vậy tập nghiệm của phương trình là S = {- 2; 5}

c) ĐKXĐ: x - 1; x 2

3(x – 2) – 2(x + 1) = 4x - 2

3x – 6 – 2x - 2 = 4x -2

– 3x = 6

x = -2 (thỏa mãn ĐKXĐ)

Vậy tập nghiệm của phương trình là S = {-2}

0,25

0.25

0,25

0,5

0,25

0,5

0,25

(2 đ)

a) $\frac{2 x+2}{3}<2+\frac{x-2}{2}$

2(2x + 2) < 12 + 3(x – 2)

4x + 4 < 12 + 3x – 6

4x – 3x < 12 – 6 – 4

x < 2

Biểu diễn tập nghiệm

b) 3x – 4 < 5x – 6

3x – 5x < - 6 +4

-2x < -2

x > -1

Vậy tập nghiệm của BPT là {x | x > -1}

0,25

0,5

0,25

0,5

0,25

(1,5 đ)

- Gọi độ dài quãng đường Viên Thành-Vinh là x (km), x > 0

- Thời gian lúc đi là: $\frac{x}{40}$ (h)

- Thời gian lúc về là: $\frac{x}{70}$ (h)

- Lập luận để có phương trình: $\frac{x}{40}\ =\ \frac{x}{70}\ +\frac{3}{4}$

- Giải phương trình được x = 70

0,25

0,5

0,25

(3,5 đ)

Vẽ hình đúng, chính xác, rõ ràng

a) Xét $\Delta \mathrm{HBA}$ và $\Delta \mathrm{ABC}$ có:

$\widehat{\mathrm{AHB}}=\widehat{\mathrm{BAC}}=90^{\circ} ; \widehat{\mathrm{ABC}}$ chung

$\Delta \mathrm{HBA} \cup \triangle \mathrm{ABC}(\mathrm{g} \cdot \mathrm{g})$

b) Áp dụng định lí Pytago trong tam giác $\mathrm{ABC}$ ta có:

$\begin{aligned} B C^{2} &=A B^{2}+A C^{2} \\ &=12^{2}+16^{2}=20^{2} \end{aligned}$

$\Rightarrow \mathrm{BC}=20 \mathrm{~cm}$

$\mathrm{Ta} có \Delta \mathrm{HBA} \cup \triangle \mathrm{ABC} \begin{array}{l} \Rightarrow \frac{A B}{B C}=\frac{A H}{A C} \Rightarrow \frac{12}{20}=\frac{A H}{16} \\ \Rightarrow \mathrm{AH}=\frac{12.16}{20}=9,6 \mathrm{~cm} \end{array}$

c) $\frac{\mathrm{EA}}{\mathrm{EB}}=\frac{\mathrm{DA}}{\mathrm{DB}}$ (vì DE là tia phân giác của $\widehat{\mathrm{ADB}}$ )

$\frac{\mathrm{FC}}{\mathrm{FA}}=\frac{\mathrm{DC}}{\mathrm{DA}}$

(vì DF là tia phân giác của $\widehat{\mathrm{ADC}}$ )

$\Rightarrow \frac{E A}{E B} \cdot \frac{F C}{F A}=\frac{D A}{D B} \cdot \frac{D C}{D A}=\frac{D C}{D B}(1)$

$\Rightarrow \frac{E A}{E B} \cdot \frac{F C}{F A} \cdot \frac{D B}{D C}=\frac{D C}{D B} \cdot \frac{D B}{D C}$

$\frac{E A}{E B} \cdot \frac{D B}{D C} \cdot \frac{F C}{F A}=1\left(\text { nhân } 2 \text { vế } v^{\prime} \dot{O} i \frac{D B}{D C}\right).$

0,5

0.5

0,25

Bài 1: Giải các phương trình sau:

1. $\frac{x+2}{x-2}-\frac{1}{x}=\frac{2}{x(x-2)}$

2. |3 x|=x+6

Bài 2 :(2,5 điểm) Một tổ sản xuất theo kế hoạch mỗi ngày phải sản xuất 50 sản phẩm.Khi thực hiện , mỗi ngày tổ sản xuất được 57 sản phẩm.Do đó tổ đã hoàn thành trước kế hoạch 1 ngày và còn vượt mức 13 sản phẩm .

Hỏi theo kế hoạch ,tổ phải sản xuất bao nhiêu sản phẩm ?

Bài 3:(3 điểm) Cho hình thang cân ABCD có AB // DC và AB< DC , đường chéo BD vuông góc với cạnh bên BC. Vẽ đường cao BH.

a/ Chứng minh BDC đồng dạng HBC

b/Cho BC=15cm ;DC= 25cm. Tính HC và HD

c/ Tính diện tích hình thang ABCD.

Bài 4 (2 điểm) Cho hình chóp tứ giác đều S. ABCD có cạnh đáy AB=10cm , cạnh bên SA=12cm.

a/Tính đường chéo AC.

b/Tính đường cao SO, rồi tính thể tích của hình chóp.

Đáp án đề thi học kì 2 lớp 8 môn Toán

Bài 1: Giải các phương trình sau: 2,5 điểm

1/ĐK :x , x 2 ( 0,25 điểm)

MTC:x(x-2) ( 0,25 điểm)

Tìm được x(x+1) = 0 ( 0,25 điểm)

X=0 hoặc x= -1 ( 0,25 điểm)

X=0 ( loại ) ( 0,25 điểm)

Vậy S= ( 0,25 điểm)

2/Nghiệm của phương trình

X=3 ( 0,5 điểm)

X= ( 0,5 điểm)

Bài 2 :( 2,5 điểm)

Gọi số ngày tổ dự định sản xuất là x ngày ,ĐK:x nguyên dương( 0,5 điểm)

Số ngày tổ thực hiện là x-1 ngày ( 0,25 điểm)

Số SP làm theo kế hoạch là 50x SP ( 0,25 điểm)

Số sản phẩm thực hiện được 57(x-1) SP ( 0,25 điểm)

Theo đầu bài ta có phương trình :

57(x-1) – 50x = 13 ( 0,5 điểm)

x= 10 ( 0,25 điểm)

Trả lời :Số ngày tổ dự định sản xuất là 10 ngày ( 0,25 điểm)

Số sản phẩm tổ sản xuất theo kế hoạch là: 50 . 10 =500 SP ( 0,25 điểm)

Bài 3: (3 điểm) Hình vẽ ( 0,25 điểm)

a/ đồng dạng (g – g) ( 0,75 điểm)

b/ HC = 9 cm ( 0,5 điểm)

HD = 16 cm ( 0,5 điểm)

c/. BH = 12 cm ( 0,25 điểm)

AB = KH = 7 cm ( 0,25 điểm)

Diện tích ABCD =192 cm2 ( 0,5 điểm)

Bài 4 :(2 điểm) Hình vẽ ( 0,25 điểm)

a/Trong tam giác vuông ABC tính $\mathrm{AC}=10 \sqrt{2}$ cm ( 0,5 điểm)

$\mathrm{SO}=\sqrt{S A^{2}-O A^{2}}=\sqrt{94} \approx 9,7 \mathrm{~cm} \quad(0,5 điểm )$

Thể tích hình chóp : $\mathrm{V} \approx 323,33 \mathrm{~cm}^{3}$ 5 điểm)

.................

Đề thi Toán lớp 8 Học kì 2 có đáp án năm 2023 - Đề 9

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 9)

Bài 1: (2 điểm) Giải bất phương trình và biểu diễn tập nghiệm trên trục số

$a/ 2-5 x \leq 17$

$b/ \frac{2-x}{3} \prec \frac{3-2 x}{5}$

Bài 2: (2điểm) Giải các phương trình sau

$a/ \frac{1}{x+2}+\frac{5}{x-2}=\frac{3 x-12}{x^{2}-4}$

b/ |x+5|=3x+1

Bài 3: (2 điểm) Một ôtô đi từ A đến B với vận tốc 60 km/h và đi từ B về A với vận tốc 45 km/h. Thời gian cả đi và về hết 7 giờ. Tính quãng đường A B

Bài 4: (2điểm) Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H

a) Chứng minh tam giác AEB đồng dạng với $\triangle A F C$ . Từ đó suy ra AF.AB=AE. AC

b) Chứng minh: $\widehat{A E F}=\widehat{A B C}$

c) Cho AE = 3cm, AB= 6cm. Chứng minh rằng SABC = 4SAEF

Bài 5: (2 điểm) Cho hình hộp chữ nhật $ABCD. A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ có A B=10 cm, B C=20cm , $A A^{\prime}=15 \mathrm{~cm}$

a/Tính diện tích toàn phần và thể tích của hình hộp chữ nhật

b/Tính độ dài đường chéo $\mathrm{AC}^{\prime}$ của hình hộp chữ nhật (làm tròn đến chữ số thập phân thứ nhất)

Đáp án đề kiểm tra học kì 2 Toán 8

Bài 1: (2 điểm) Giải bất phương trình và biểu diễn tập nghiệm trên trục số

$a. 2-5 x \leq 17$

$-5 x \leq 15$

$x \geq-3$

Vây: Nghiệm của bất phương trình là $x \geq-3$

Biểu diễn tập nghiệm của bất phương trình trên trục số

$b. \frac{2-x}{3} \prec \frac{3-2 x}{5}$

5(2-x)<3(3-2 x)

$x<-1 \text { - } 3(3-2 x)$

Vây: Nghiệm của bất phương trình là x<-1

Câu 2

$a. \frac{1}{x+2}+\frac{5}{x-2}=\frac{3 x-12}{x^{2}-4}$

ĐKXĐ: $x \neq \pm 2$

$\begin{aligned} & \frac{1}{x+2}+\frac{5}{x-2}=\frac{3 x-12}{x^{2}-4} \\ \Leftrightarrow & x-2+5(x+2)=3 x-12 \end{aligned}$

$\begin{aligned} &\Leftrightarrow 3 \mathrm{x}=-20 \\ &\Leftrightarrow \mathrm{x}=\frac{-20}{3} \end{aligned}$

Vậy: Tập nghiệm của phương trình $S=\left\{\frac{-20}{3}\right\}$

b. |x+5|=3 x+1

TH1: $x+5=3 x+1 với x \geq-5$

x=2 (nhận)

TH2: -x-5=3 x+1 với x<-5

$x=\frac{-3}{2} \text { (loai ) }$

Goi x(k m) là quãng đường A B(x>0)

Thời gian đi từ A đến B là : $\frac{x}{60}(h)$

Thời gian đi từ B về A là: $\frac{x}{45}(h)$

Theo đề bài ta có phương trình: $\frac{x}{60}+\frac{x}{45}=7$

Giải phương trình được x =180 (nhân)

Quãng đường AB dài 180km

Đề thi Toán lớp 8 Học kì 2 có đáp án năm 20223 - Đề 10

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 10)

Bài 1: (2,0 điểm) giải phương trình:

$a / \frac{5 x-2}{3}+x=1+\frac{5-3 x}{2}$

$b /(x+2)(3-4 x)=x^{2}+4 x+4$

Bài 2: (2 điểm)

a/ Tìm x sao cho giá tri của biểu thức $\frac{2 x^{2}-3 x-2}{x^{2}-4}$ bằng 2

b/ Tìm x sao cho giá trị của hai biểu thức

$\frac{6 x-1}{3 x+2} và \frac{2 x+5}{x-3}$ bằng nhau

Bài 3: (2,0 điểm)

a/ giải bất phương trình: 3(x - 2)(x + 2) < 3x² + x

b/ Giải phương trình: = I5x - 4I = 4 - 5x

Bài 4: (2,0 điểm) Một phân số có tử số bé hơn mẫu số là 11. Nếu tăng tử số lên 3 đơn vị và giảm mẫu số đi 4 đơn vị thì được một phân số bằng $\frac{3}{4}$ . Tìm phân số ban đầu?

Bài 5: (2,0 điểm) Tam giác ABC có hai đường cao là AD và BE (D thuộc BC và E thuộc AC).

Chứng minh hai tam giác DEC và ABC là hai tam giác đồng dạng?

Đáp án đề thi học kì 2 Toán 8

Câu 1

a/ Giải phương trình:

$\begin{aligned} \frac{5 x-2}{3}+x=1+\frac{5-3 x}{2} & \Leftrightarrow 10 x+6 x+9 x=6+15+4 \\ & \Leftrightarrow x=1 \quad S=\{1\} \end{aligned}$

b/ Giải phương trình:

$\begin{gathered} (\mathrm{x}+2)(3-4 \mathrm{x})=\mathrm{x}^{2}+4 \mathrm{x}+4 \Leftrightarrow(x+2)(1-5 x)=0 \\ \mathrm{~S}=\left\{-2 ; \frac{1}{5}\right\} \end{gathered}$