Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu bài tập Trắc nghiệm Ứng dụng của tích phân Toán lớp 12, tài liệu bao gồm 34 trang, tuyển chọn 76 bài tập trắc nghiệm Ứng dụng của tích phân có đáp án và lời giải chi tiết, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi tốt nghiệp THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu 76 câu trắc nghiệm Ứng dụng của tích phân có đáp án có nội dung chính sau:

- Gồm 76 câu hỏi vận dụng có đáp án và lời giải chi tiết giúp học sinh tự rèn luyện cách giải các bài tập Ứng dụng của tích phân

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

Trắc nghiệm Ứng dụng hình học của tích phân có đáp án – Toán 12

Câu 1: Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục Ox và hai đường thẳng x = a, x = b (a < b) quanh trục Ox.

Câu 2: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số x³ - x và đồ thị hàm số y = x - x².

Tìm hoành độ các giao điểm của hai đồ thị, ta có:

x³ - x = x - x³ <=> x³ + x² - 2x = 0

Vậy diện tích của hình phẳng tính là

Vậy chọn đáp án B.

Câu 3: Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = (x -1)e^2x ,trục tung và đường thẳng y = 0. Tính thể tích của khối tròn xoay thu được khi quay hình (H) quanh trục Ox

Tìm hoành độ giao điểm của hai dồ thị, ta có:

(x - 1)e^2x = 0 => x = 1

Vậy thể tích của khối tròn xoay thu được khi quay (H) quanh Ox được tính bởi

Đặt: u = (x - 1)², dv e^4xdx. Ta có du = 2(x -1)dx và v = e^4x/4 .

Áp dụng công thức tích phân từng phần ta được

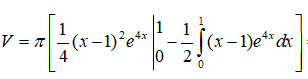
Đặt u₁ = x - 1, dv₁ = e^4xdx , ta có du₁ = dx, v₁ = e^4x/4 .

Vậy chọn đáp án A.

Câu 4: Sau chiến tranh thế giới thứ hai, tốc độ sinh ở cả nước phương Tây tăng rất nhanh. Giả sử rằng tốc độ sinh được cho bởi: b(t) = 5 + 2t, 0 ≤ t ≤ 10 , ( ở đó t số năm tính từ khi chiến tranh kết thúc, b(t) tính theo đơn vị triệu người).

a) Có bao nhiêu trẻ được sinh trong khoảng thời gian này ( tức là trong 10 năm đầu tiên sau chiến tranh)?

A. 100 triệu     B. 120 triệu     C. 150 triệu     D. 250 triệu.

b) Tìm khoảng thời gian T sao cho số lượng trẻ được sinh ra là 14 triệu kể từ khi kết thức chiến tranh.

A. 1 năm     B. 2 năm     C. 3 năm     D. 4 năm.

a) Để tìm số trẻ mới sinh, chúng ta sẽ tính tích phân tỉ lệ sinh b(t) trên khoảng thời gian 10 năm đầu tiên sau chiến tranh

Vậy số trẻ được sinh cần tìm là 150 triệu.

Chọn đáp án C.

b) Số lượng trẻ mới sinh trong khoảng thời T bằng:

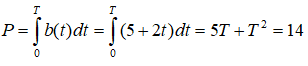
Vậy chọn đáp án B.

Câu 5: Diện tích hình phẳng giới hạn bởi y = x² - x + 3 và y = 2x + 1 là:

Ta có: x² - x + 3 = 2x + 1 <=> x² - 3x + 2 = 0 <=> x = 2 hoặc x = 1

Câu 6: Cho đồ thị hàm số y = f(x). Diện tích hình phẳng ( phần gạch sọc ) là:

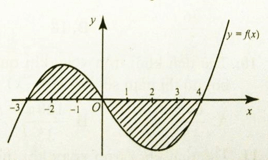
Câu 7: Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số y = √6 và y = 6 - x và trục tùng là:

Diện tích giới hạn được tính bởi

Câu 8: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x + 1/x , trục hoành, đường thẳng x = -1 và đường thẳng x = -2 là:

Câu 9: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = e^x - e^-x , trục hoành, đường thẳng x = -1 và đường thẳng x = 1.

Diện tích hình phẳng được tính bởi

Câu 10: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = √x - x và trục hoành.

Xét phương trình

Khi đó diện tích hình phẳng được tính bởi

Câu 11: Gọi h(t) (cm) là mức nước ở bồn chứa sau khi bơm nước được t giây. Biết rằng

và lúc đầu bồn không có nước. Mức nước ở bồn sau khi bơm nước được 6 giây xấp xỉ bằng:

A. 2,65cm     B. 2,66cm     C. 2,67cm     D. 2,68cm.

Mức nước trong bồn tại giây thứ t bằng:

Khi đó h(6) ≈ 2,66 cm .

Câu 12: Vận tốc của một vật chuyển động là

Quãng đường vật di chuyển trong khoảng thời gian 1,5 giây xấp xỉ bằng:

A. 0,33m     B. 0,34m     C. 0,35m     D. 0,36m.

Quãng đường vật di chuyển sau thời gian 1,5 giây bằng

Câu 13: Thể tích phần vật thể giới hạn bởi hai mặt phẳng x = 0 và x = 3 biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x(0 ≤ x ≤ 3) là một hình chữ nhật có hai kích thước là x và 2√(9-x²)

Câu 14: Thể tích khối xoay khi quay quanh trục hoành một hình phẳng giới hạn bởi đồ thị hàm số y = x(x-4) và trục hoành là:

Phương trình hoành độ giao điểm của đồ thị và trục hoành :

Câu 15: Thể tích khối tròn khi quay quanh trục hoành một hình phẳng giới hạn bởi đồ thị hàm số y = sinxcosx, y = 0, x = 0, x = π/2 là:

Thể tích khối tròn xoay là :

Câu 16: Thể tích khối tròn xoay khi quay quanh trục hoành một hình phẳng giới hạn bởi đồ thị hàm số y = lnx, y = 0, x = 2 là:

A. π(ln²2 - 2ln2 + 1)     B. 2π(ln²2 - 2ln2 + 1)

C. 4π(ln²2 - ln2 + 1)    D. 2π(ln²2 - ln2 + 1)

Phương trình giao điểm của đồ thị hàm số và trục hoành :

ln x = 0 ⇔ x = 1

Thể tích khối tròn xoay cần tính là :

Câu 17: Thể tích khối tròn xoay khi quay quanh trục tung một hình phẳng giới hạn bởi hình tròn tâm I(2;0) bán kính R = 1 là:

A. π²     B. 2π²     C. 4π²     D. 8π²

Phương trình đường tròn tâm I(2 ; 0), bán kính R = 1 là :

Đường tròn cắt trục tung tại hai điểm (0; 1) và( 0; -1).

Vậy ta có:

Câu 18. Công thức tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số $y=f\left(x\right),y=g\left(x\right)$, liên tục trên $\left[a;b\right]$ và hai đường thẳng $x=a; x=b \left(a<b\right)$  là:

A. $S=\pi {\int }_a^b|f\left(x\right)-g\left(x\right)|.dx$.                          B. $S={\int }_a^b(f\left(x\right)-g\left(x\right))𝑑x$.

C. $S={\int }_a^b{(f\left(x\right)-g\left(x\right))}^2.dx$                           D. $S={\int }_a^b|f\left(x\right)-g\left(x\right)|.dx$

Câu 19. Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số $y=f\left(x\right)$, liên tục trên $\left[a;b\right]$ trục hoành và hai đường thẳng $x=a; x=b \left(a<b\right)$ cho bởi công thức:

A. $S=\underset{a}{\overset{b}{\int }}|f\left(x\right)|𝑑x.$     B. $S=\underset{a}{\overset{b}{\int }}f\left(x\right)𝑑x.$      C. $S=\pi \underset{a}{\overset{b}{\int }}|f\left(x\right)|𝑑x.$    D.$S=\pi \underset{a}{\overset{b}{\int }}{f}^2\left(x\right)𝑑x.$

Câu 20. Diện tích hình phẳng giới hạn bởi các đường $y=x^3+11x-6,y=6x^2$, $x=0,x=2$. (Đơn vị diện tích)

A.   $\frac{4}{3}$                      B.   $\frac{5}{2}$                     C.  $\frac{8}{3}$                      D. $\frac{18}{23}$

Câu 21. Diện tích hình phẳng giới hạn bởi $y=x^3,y=4x$ là:

A. 8                          B. 9                        C. 12                      D. 13

Câu 22.  Cho hàm số $y=f\left(x\right)$ liên tục và nhận giá trị không âm trên đoạn $\left[a;b\right]$. Diện tích hình thang cong giới hạn bởi đồ thị của $y=f\left(x\right)$, trục hoành và hai đường thẳng $x=a; x=b$,  được tính theo công thức 

A.  $S=\underset{a}{\overset{b}{\int }}f\left(x\right)𝑑x.$         B.  $S=-\underset{a}{\overset{b}{\int }}f\left(x\right)𝑑x.$     C. $S=-\underset{a}{\overset{b}{\int }}{f}^2\left(x\right)𝑑x.$     D. $S=\underset{a}{\overset{b}{\int }}{f}^2\left(x\right)𝑑x.$

Câu 23.  Diện tích hình phẳng được giới hạn bởi đồ thị của hàm số $y=f\left(x\right)$ liên tục trên đoạn $\left[a;b\right]$, trục hoành và hai đường thẳng $x=a; x=b$,  được tính theo công thức

A. $S=\underset{a}{\overset{b}{\int }}|f\left(x\right)|𝑑x.$        B. $S=\underset{a}{\overset{b}{\int }}f\left(x\right)𝑑x.$        C. $S=\underset{a}{\overset{b}{\int }}{|f\left(x\right)|}^2𝑑x.$     D. $S=\pi \underset{a}{\overset{b}{\int }}f\left(x\right)𝑑x.$

Câu 24. Diện tích hình phẳng được giới hạn bởi đồ thị các hàm số $y=f\left(x\right), y=g\left(x\right)$,  liên tục trên đoạn $\left[a;b\right]$, trục hoành và hai đường thẳng $x=a; x=b$ được tính theo công thức

A.  $S=\underset{a}{\overset{b}{\int }}{|f\left(x\right)-g\left(x\right)|}^2𝑑x.$                            B. $S=\underset{a}{\overset{b}{\int }}[f\left(x\right)-g\left(x\right)]𝑑x.$       

C.  $S=\underset{a}{\overset{b}{\int }}|f\left(x\right)-g\left(x\right)|𝑑x.$                             D. $S=\pi \underset{a}{\overset{b}{\int }}{|f\left(x\right)-g\left(x\right)|}^2𝑑x.$