Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 12 Bài 3: Ứng dụng tích phân trong hình học chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Ứng dụng tích phân trong hình học lớp 12.
Giải bài tập Toán lớp 12 Bài 3: Ứng dụng tích phân trong hình học
Trả lời câu hỏi giữa bài
Trả lời câu hỏi 1 trang 114 SGK Giải tích 12: Tính diện tích hình thang vuông được giới hạn các đường thẳng và .
So sánh với diện tích hình thang vuông trong câu hỏi 1 bài 2.
Phương pháp giải:
Lời giải:
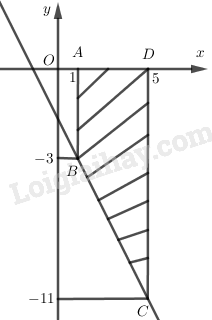
Gọi .
là giao điểm của đường thẳng với đường thẳng thì
là giao điểm của đường thẳng với đường thẳng thì
Diện tích hình thang .
Trả lời câu hỏi 2 trang 117 SGK Giải tích 12: Hãy nhắc lại công thức tính thể tích khối lăng trụ có diện tích đáy bằng và chiều cao bằng .
Lời giải:
Công thức tính thể tích lăng trụ có diện tích đáy là và chiều cao là: .
Lời giải:
- Khái niệm mặt tròn xoay:
Trong không gian cho mặt phẳng chứa đường thẳng và một đường C . Khi quay mặt phẳng quanh một góc thì mỗi điểm trên đường C vạch ra một đường tròn có tâm thuộc và nằm trên mặt phẳng vuông góc với . Như vậy khi quay mặt phẳng quanh đường thẳng thì đường C sẽ tao nên một hình được goi là mặt tròn xoay.
Đường C được gọi là đường sinh của mặt tròn xoay đó. Đường thẳng được gọi là trục của mặt tròn xoay.

- Khái niệm khối tròn xoay: Khối tròn xoay là khối hình học được tạo thành khi quay một hình phẳng quanh một đường thẳng cố định (trục quay) của hình.

a) ;
Phương pháp giải:
Cho hai hàm số liên tục trên đoạn . Gọi là hình phẳng được giới hạn bởi đồ thị hai hàm số trên và các đường thẳng . Khi đó diện tích của hình phẳng được tính bởi công thức:
Lời giải:
a)
Phương trình hoành độ giao điểm của hai đồ thị là:
Diện tích hình phẳng cần tìm là:
(đvdt).
b)
Phương trình hoành độ giao điểm của hai đồ thị là:
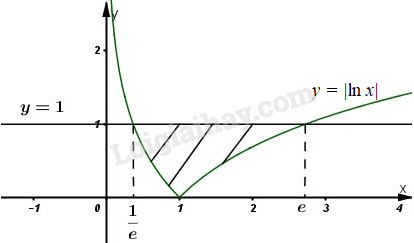
Ta có: nếu , tức là .
hoặc nếu , tức là .
Dựa vào đồ thị hàm số vẽ ở hình trên ta có diện tích cần tìm là :
Tính ta có:
Đặt
Do đó , thay vào trên ta được:
(đvdt).
c)
Phương trình hoành độ giao điểm của hai đồ thị là:
Diện tích cần tìm là:
.
Phương pháp giải:
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm theo công thức:
+) Xét phương trình hoành độ giao điểm, tìm nghiệm.
+) Tính diện tích hình phẳng thông qua tích phân.
Lời giải:
Ta có:
Phương trình tiếp tuyến của đồ thị hàm số tại là:
Phương trình tiếp tuyến là .
Phương trình hoành độ giao điểm của đồ thị hàm số với tiếp tuyến là:
Do đó diện tích phải tìm là:
.
Phương pháp giải:
+) Xác định các phần của đường tròn được chia bởi parabol (P).
+) Sử dụng công thức tính diện tích hình phẳng để tính diện tích hai phần được chia sau đó tính tỉ số của hai phần diện tích.
Lời giải:
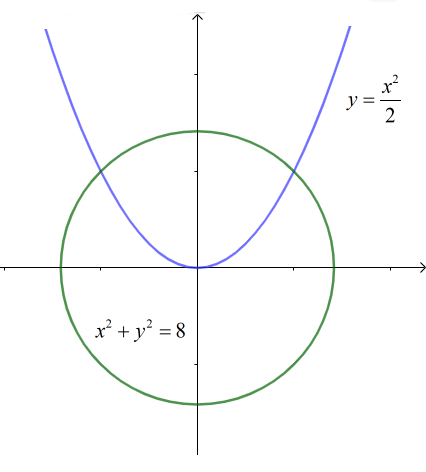
Đường tròn đã cho có phương trình:
Từ đó ta có:
Tọa độ giao điểm của và là nghiệm của hệ phương trình:

Gọi và là diện tích hai phần của đường tròn được chia bởi parabol như hình vẽ.
Khi đó ta có:
Tính
Đặt
Đổi cận:
Tính
Do đó
Diện tích hình tròn là:
Vậy hay
a) , ;
Phương pháp giải:
Cho hình phẳng được giới hạn bởi hai đồ thị hàm số và hai đường thẳng Khi quay hình phẳng trên quanh trục ta được khối tròn xoay có thể tích được tính bởi công thức:
Lời giải:
a)
Phương trình hoành độ giao điểm của hai đồ thị hàm số là: .
Khi đó thể tích khối tròn xoay cần tìm là:
b)
Thể tích cần tìm là:
c)
Thể tích cần tìm là:
.
và ,
Gọi 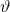 là khối tròn xoay thu được khi quay tam giác đó xung quanh (H.63).
là khối tròn xoay thu được khi quay tam giác đó xung quanh (H.63).
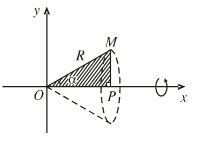
a) Tính thể tích của 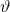 theo và .
theo và .
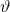 là lớn nhất.
là lớn nhất.Phương pháp giải:
a) Hình phẳng cần tính thể tích được giới hạn bởi đoạn thẳng và trục hoành.
+) Xác định phương trình đường thẳng và sử dụng công thức tính thể tích để tính thể tích khối tròn xoay 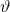 cần tính.
cần tính.
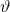 theo Khảo sát hàm số để tìm thể tích lớn nhất.
theo Khảo sát hàm số để tìm thể tích lớn nhất.Lời giải:
a)
Ta có:
Điểm thuộc đường thẳng
Mà cũng thuộc đường thẳng trên nên phương trình đường thẳng là
Khi đó thể tích của khối tròn xoay là:
Cách khác:
Ta có:
Khi quay tam giác quanh trục ta được khối nón tròn xoay có bán kính đáy và chiều cao
Thể tích khối nón là:
b)
Xét hàm số:
Đặt
Với
Khi đó ta xét hàm: trên
Có:
Ta có bảng biến thiên:
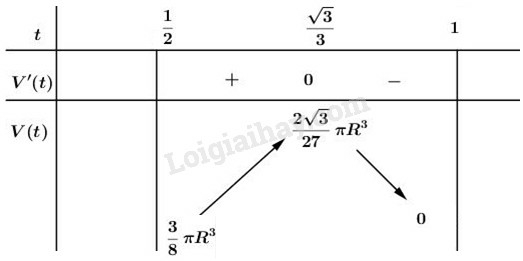
Hàm số đạt giá trị lớn nhất khi .
Vậy thể tích khối 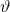 lớn nhất khi
lớn nhất khi
1. Tính diện tích hình phẳng
a) Nếu hình phẳng được giới hạn bởi đồ thị hàm số liên tục trên đoạn ; trục hoành và hai đường thẳng , thì diện tích được cho bởi công thức:
(1)
Chú ý: Để tính tích phân trên, ta xét dấu của trên đoạn . Nếu không đổi dấu trên khoảng thì :
Chẳng hạn ta có:
b) Nếu hình phẳng được giới hạn bởi đồ thị của hai hàm số và liên tục trên đoạn [a;b] và hai đường thẳng thì diện tích được cho bởi công thức :
(2)
Chú ý: Để tính tích phân trên, ta xét dấu trên đoạn hoặc tìm nghiệm của nó trên khoảng , sau đó áp dụng tính chất nêu ở chú ý trên. Cụ thể ta thực hiện các bước sau:
Bước 1: Giải phương trình: , tìm các nghiệm
Bước 2 : Sắp xếp các nghiệm theo thứ tự tăng dần, chẳng hạn có n nghiệm:
Bước 3: Tính diện tích theo công thức (*):
Nếu hình phẳng nói trên không cho giới hạn bởi hai đường thẳng thì ta tìm các nghiệm trên tập xác định và trong công thức (*), a được thay thế bởi , b được thay thế bởi .
Công thức (1) là trường hợp đặc biệt của công thức (2) khi hoặc
Tương tự, hình phẳng được giới hạn bởi đồ thị hàm số liên tục trên đoạn và hai đường thẳng có diện tích được cho bởi công thức:
2. Thể tích vật thể
Một vật thể được giới hạn bởi hai mặt phẳng vuông góc với trục hoành tại điểm có hoành độ . là diện tích của thiết diện. Thể tích của vật thể được cho bởi công thức: (với là hàm số không âm, liên tục trên đoạn ).

3. Thể tích khối tròn xoay
a) Hình phẳng quay quanh trục : Cho hình phẳng được giới hạn bởi đồ thị hàm số không âm và liên tục trên đoạn , trục và hai đường thẳng quay quanh trục , ta được khối tròn xoay (h.4). Thể tích của khối tròn xoay này được cho bởi công thức:
b) Hình phẳng quay quanh trục (kiến thức bổ sung): Cho hình phẳng được giới hạn bởi đồ thị hàm số không âm và liên tục trên đoạn , trục và hai đường thẳng quay quanh trục , ta được khối tròn xoay. Thể tích Vy của khối tròn xoay này được cho bởi công thức:
Chú ý. Thể tích của vật thể tạo bởi hình phẳng được giới hạn bởi hai đường thẳng , và đồ thị hàm số liên tục và trên đoạn quay quanh trục được cho bởi công thức:
Tương tự, đổi vai trò và cho nhau, ta có công thức tính (khi hình phẳng quay quanh trục ).
Sơ đồ tư duy về ứng dụng tích phân trong hình học
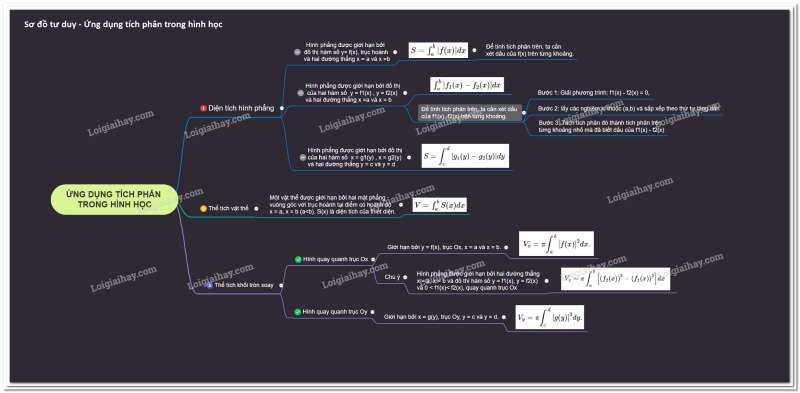
1. Ứng dụng của tích phân trong hình học (diện tích hình phẳng)
Dạng 1: Tính diện tích hình phẳng nếu biết hai đường giới hạn
Phương pháp:
- Diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục và hai đường thẳng được tính bởi công thức:
- Diện tích hình phẳng giới hạn bởi đồ thị hàm số và hai đường thẳng được tính bởi công thức:
Dạng 2: Tính diện tích hình phẳng nếu chưa biết hai đường giới hạn
Phương pháp:
- Bước 1: Giải phương trình tìm nghiệm.
- Bước 2: Phá dấu giá trị tuyệt đối của biểu thức
- Bước 3: Tính diện tích hình phẳng theo công thức tích phân:
Ví dụ: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và các trục tọa độ. Chọn kết quả đúng nhất.
A.
B.
C.
D.
Giải:
Đồ thị hàm số cắt tại , cắt tại .
Hàm số có nên hàm số nghịch biến trên .
Do đó
Do đó
Chọn D.
2. Ứng dụng của tích phân trong hình học (thể tích vật thể)
Dạng 1: Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số , trục và hai đường thẳng quanh trục
Công thức tính:
Dạng 2: Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số , trục và hai đường thẳng quanh trục .
Công thức tính:
Dạng 3: Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đồ thị hàm số liên tục trên quay quanh trục
Công thức tính:
Dạng 4 (Đọc thêm): Tính thể tích của vật thể giới hạn bởi các mặt phẳng biết diện tích thiết diện cắt bởi mặt phẳng vuông góc trục là .
Công thức tính:
Khi miền giới hạn bởi nhiều đồ thị hàm số thì ta nên vẽ hình, sau đó từ hình vẽ suy ra cách tính.
Ví dụ: Cho đường cong và đường thẳng . Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi hai đường trên quanh .
Ta có:
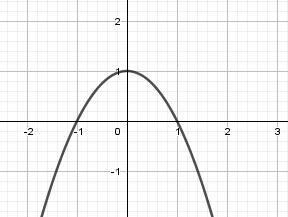
Thể tích:
.