Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Lý thuyết Đồ thị hàm số Toán lớp 12, tài liệu bao gồm 4 trang, tổng hợp lí thuyết về các dạng đồ thị hàm số thường gặp, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi tốt nghiệp THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:
LÝ THUYẾT VỀ ĐỒ THỊ HÀM SỐ
1. Các bước khảo sát và vẽ đồ thị hàm số y = f(x)
I) Tìm tập xác định của hàm số.
II) Sự biến thiên
+ Xét sự biến thiên của hàm số
- Tìm đạo hàm bậc nhất ;
- Tìm các điểm tại đó bằng 0 hoặc không xác định ;
- Xét dấu và suy ra chiều biến thiên của hàm số.
+ Tìm cực trị.
+ Tìm các giới hạn tại vô cực, các giới hạn vô cực và tìm các tiệm cận (nếu có).
+ Lập bảng biến thiên tổng kết các bước trên để hình dung ra dáng điệu của đồ thị
III) Vẽ đồ thị (thể hiện các cực trị, tiệm cận, giao của đồ thị với các trục, . . .)
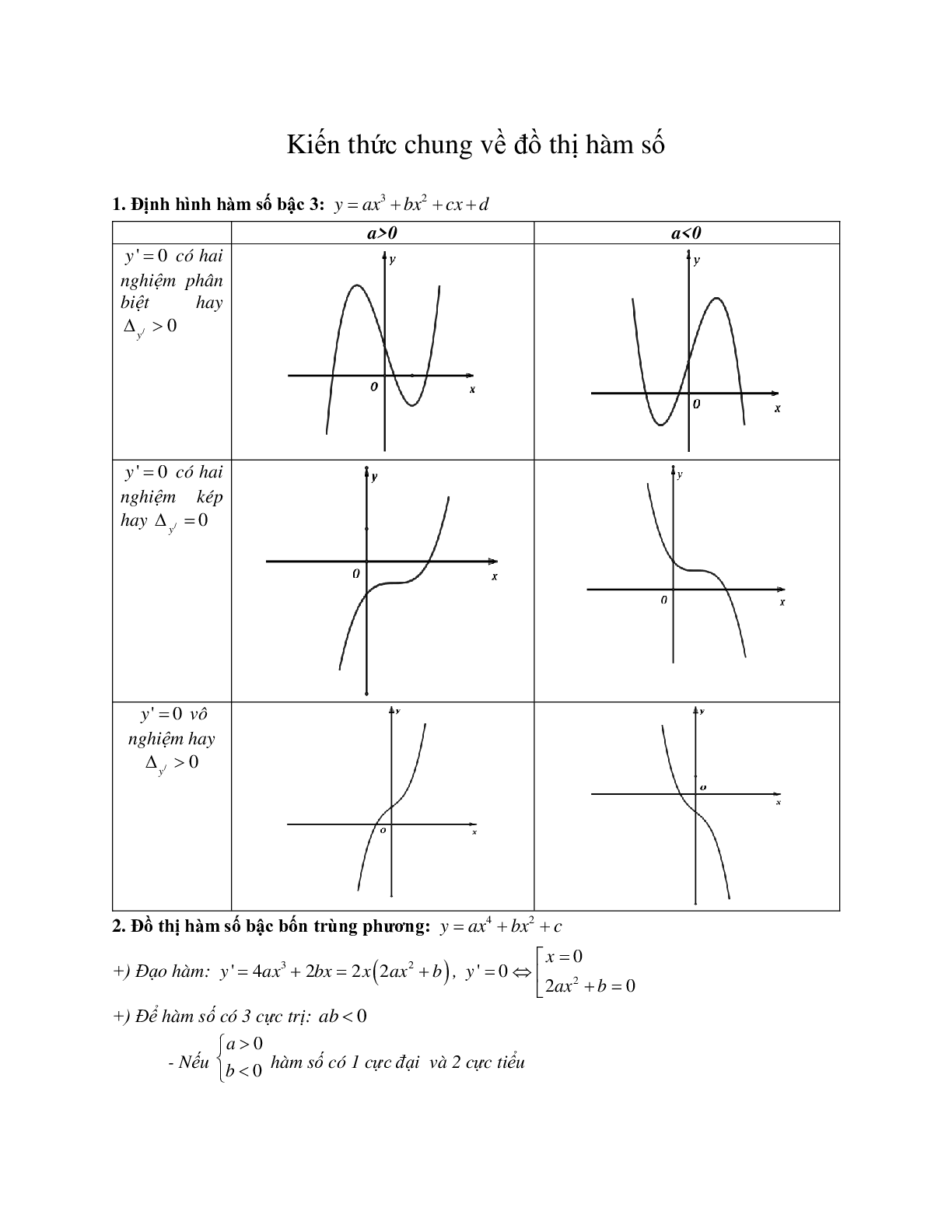
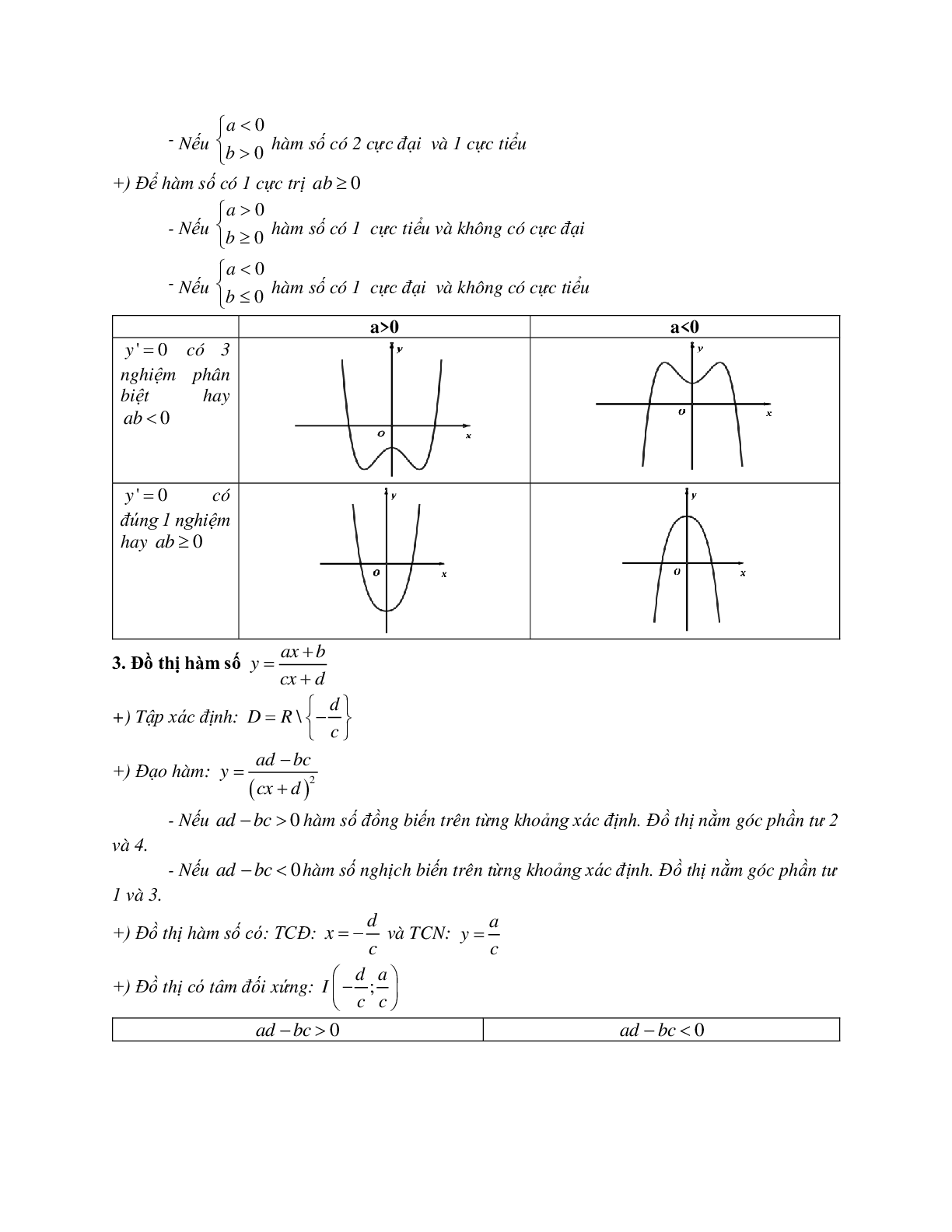
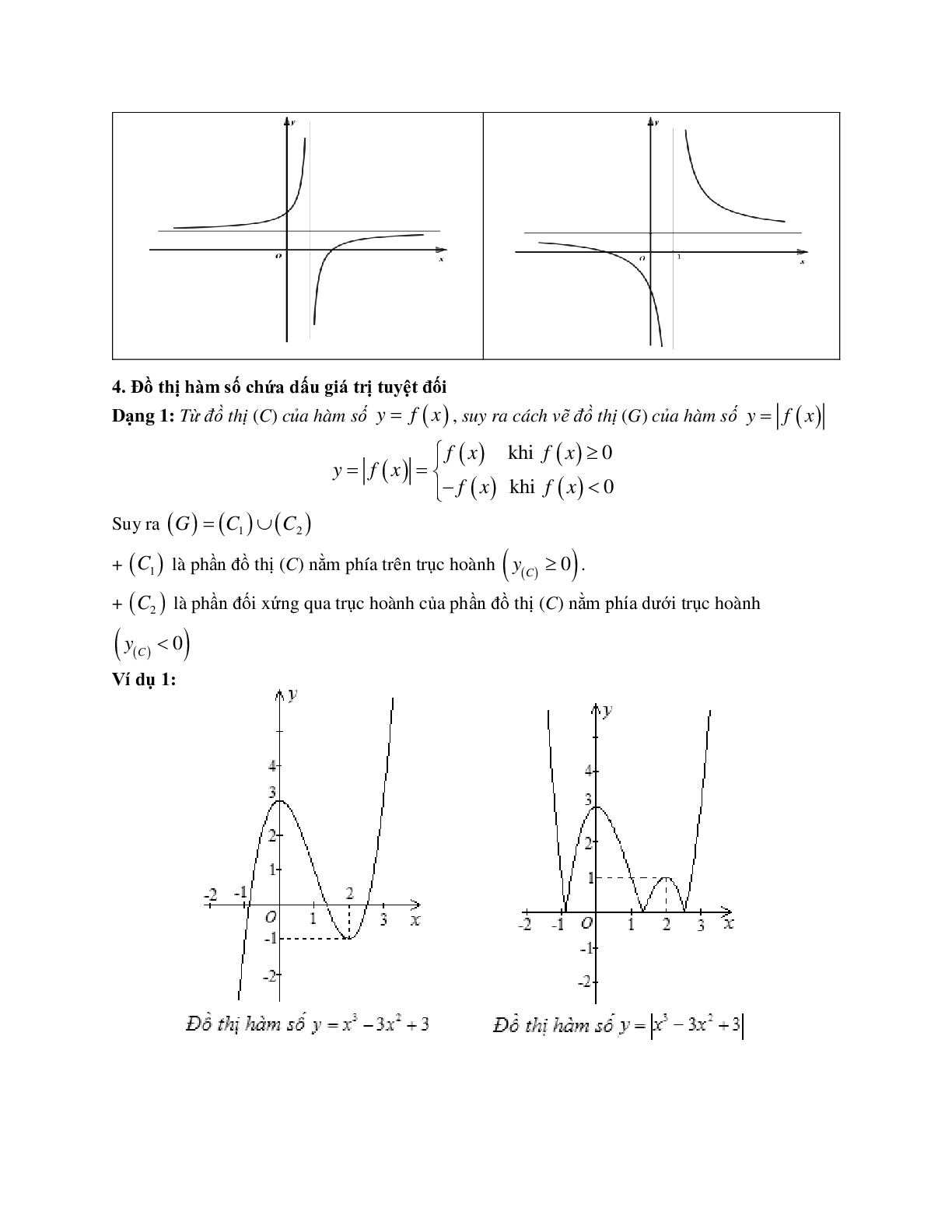
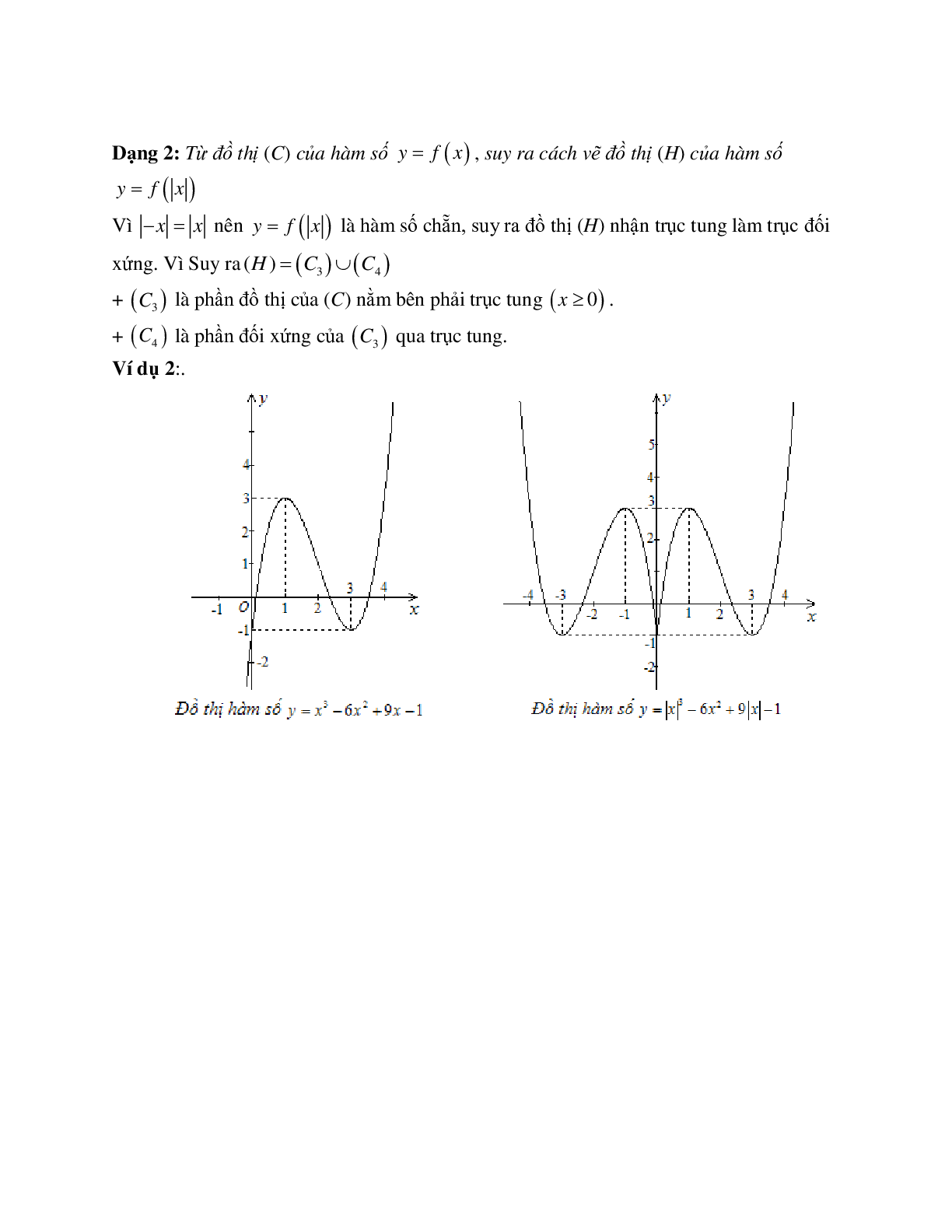
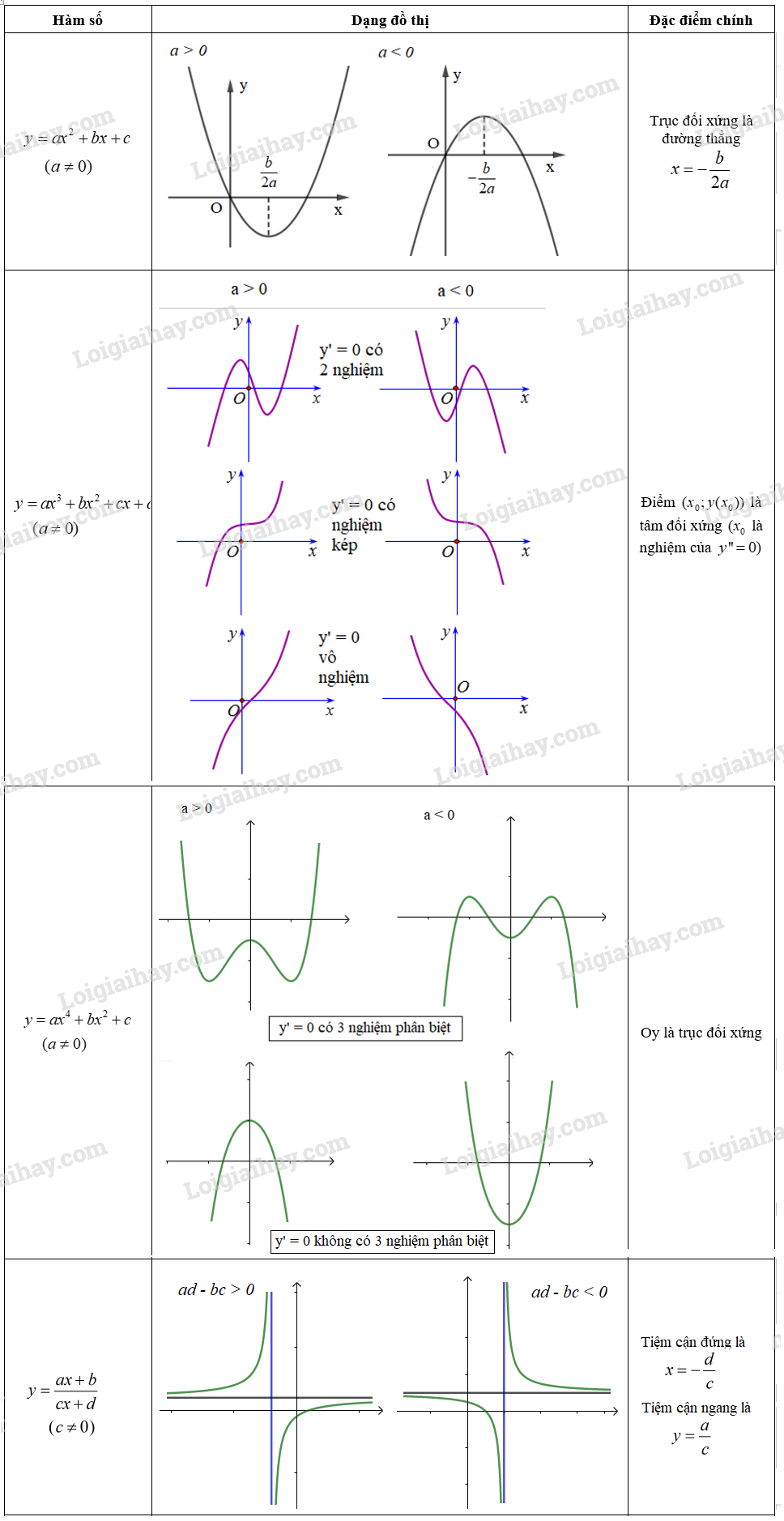
2. Bảng tóm tắt một số dạng đồ thị thường gặp
3. Tương giao của các đồ thị
Cho hai đồ thị và
Phương trình xác định hoành độ giao điểm của và là: (1)
- Nếu (1) vô nghiệm thì và không có điểm chung (không cắt nhau và không tiếp xúc với nhau).
- Nếu (1) có nghiệm phân biệt thì và giao nhau tại điểm phân biệt. Nghiệm của (1) chính là hoành độ các giao điểm.
Chú ý
a) tiếp xúc với hệ có nghiệm. Nghiệm của hệ là hoành độ tiếp điểm của hai đồ thị đó.
b) Đường thẳng (d): y: mx+n tiếp xúc với parabol ()
hệ có nghiệm
phương trình có nghiệm kép.
B. BÀI TẬP VỀ ĐỒ THỊ HÀM SỐ
Câu 1. Đồ thị của hàm số dưới đây có dạng như đường cong bên?
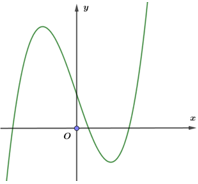
A.
B.
C.
D. .
Câu 2. Đồ thị hình bên là của hàm số nào?
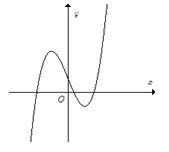
A.
B. .
C.
D. .
Câu 3. Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào ?
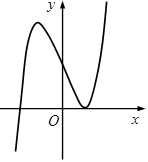
A.
B.
C.
D.
Câu 4. Đồ thị sau đây là của hàm số nào?
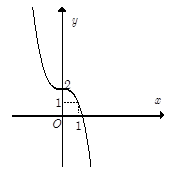
A.
B. .
C.
D. .
Câu 5. Cho hàm số có bảng biến thiên sau:
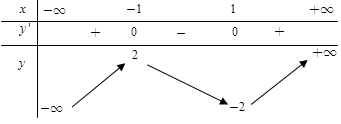
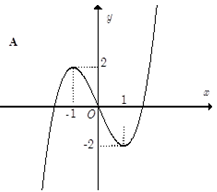
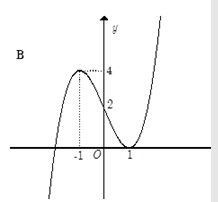
Đồ thị nào sau đây thể hiện hàm số y = f(x)?
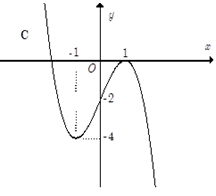
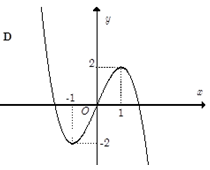
Câu 6. Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào ?
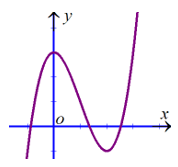
A. y = 2x + 5.
B. x =2 .
C. x = -5
D. .
Câu 7. Cho hàm số có đồ thị như hình bên. Chọn đáp án đúng?
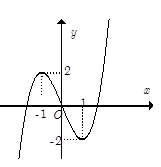
A. Hàm số có hệ số a <0.
B. Hàm số đồng biến trên các khoảng (2-;1) và (1;2).
C. Hàm số không có cực trị.
D. Hệ số tự do của hàm số khác 0.
Câu 8. Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào ?
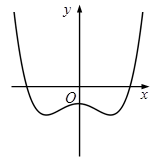
A.
B. .
C.
D. .
Câu 9. Đồ thị sau đây là của hàm số nào?
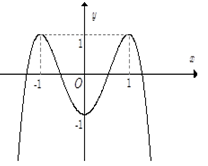
A.
B.
C.
D. .
Câu 10. Đồ thị hình bên là của hàm số nào?
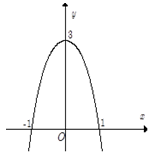
A.
B. .
C.
D. .
Câu 11. Đồ thị sau đây là của hàm số nào?
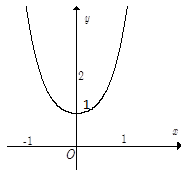
A.
B. .
C.
D. .
Câu 12. Trong các đồ thị hàm số sau, đồ thị nào là đồ thị của hàm số ?
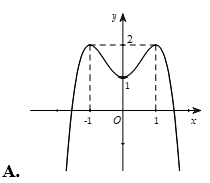
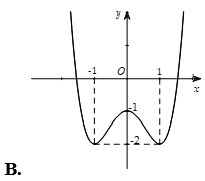
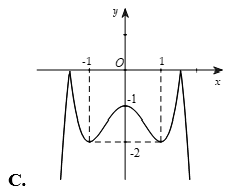
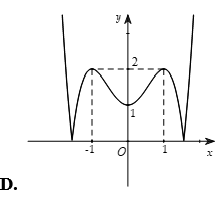
Câu 13. Đồ thị sau đây là của hàm số nào?
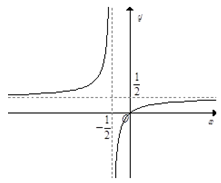
A.
B.
C.
D.
Câu 14. Đường cong ở hình bên là đồ thị của hàm số với a, b, c, d là các số thực. Mệnh đề nào dưới đây đúng ?
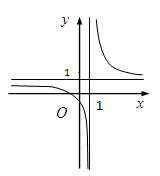
A.
B.
C.
D.
Câu 15. Cho hàm số có đồ thị như Hình 1. Đồ thị Hình 2 là của hàm số nào dưới đây?
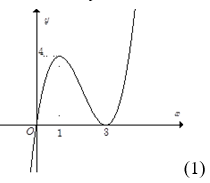
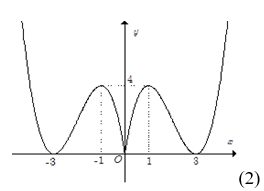
A.
B.
C.
D.
Câu 16. Đồ thị hàm số cắt trục hoành tại mấy điểm?
A. 2
B. 3
C. 1
D. 0.
Câu 17. Cho hàm số có đồ thị (C) và đường thẳng d:. Số giao điểm của (C) và d là
A. 0.
B. 1
C. 2
D. 3
Câu 18. Số giao điểm của đồ thị hàm số và trục hoành là
A. 0.
B. 1
C. 3
D. 2
Câu 19. Số giao điểm của đồ thị hàm số và trục hoành là
A. 0.
B. 1
C. 3
D. 2.
Câu 20. Cho hàm số f(x) = ax3 + bx2 + cx + d (a,b,c,d ∈ R) có bảng biến thiên như sau:
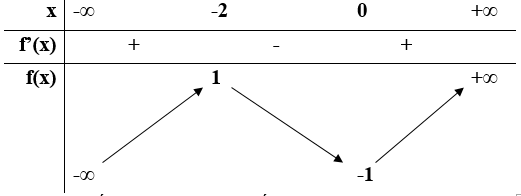
Có bao nhiêu số dương trong các số a,b,c,d
A. 3 B. 4 C. 2 D. 1
Lời giải
Chọn C
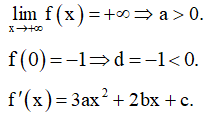
Ta có 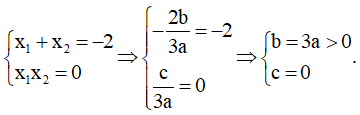
Vậy có 2 giá trị dương là a và b.
Câu 21. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
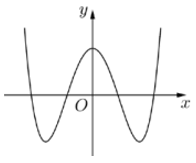
A. y = x3 - 3x + 1 B. y = -2x4 + 4x2 + 1
C. y = -x3 + 3x + 1 D. y = 2x4 - 4x2 + 1
Lời giải
Từ đồ thị ta thấy:
- Đây là đồ thị hàm bậc 4 trùng phương
- Đồ thị hàm số có dạng hình chữ w nên a > 0
Chọn D.
Câu 22. Cho hàm số 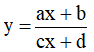 có bảng biến thiên như hình vẽ bên. Hỏi hàm số đã cho là hàm số nào?
có bảng biến thiên như hình vẽ bên. Hỏi hàm số đã cho là hàm số nào?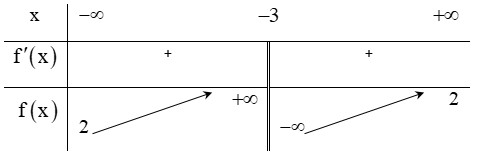
Lời giải
Dựa vào bảng biến thiên ta thấy:
+ Đồ thị hàm số nhận đường thẳng x = -3 là tiệm cận đứng và đường thẳng y = 2 là tiệm cận ngang (loại đáp án A và B).
+ Hàm số đã cho đồng biến trên mỗi khoảng xác định.
Xét hàm số 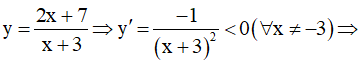 Hàm số nghịch biến trên mỗi khoảng xác định nên ta loại đáp án C.
Hàm số nghịch biến trên mỗi khoảng xác định nên ta loại đáp án C.
Chọn D.