Trong các hàm số sau, hàm số nào luôn đồng biến trên từng khoảng xác định của nó?
(I) ; y = -x4 + x2 – 2 (II); y = x3 – 3x – 5 (III).
A. I và II
B. Chỉ I
C. I và III
D. II và III
Giải bởi Vietjack
Chọn B.
Hàm số (I): 
, ∀x ∈ D = R \ {-1} nên hàm số đồng biến trên từng khoảng xác định của nó.
Hàm số (II): y’ = -4x3 + 2x. y' = 0 <=> - 4x3 + 2x = 0 <=>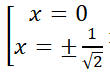 
nên hàm số không đồng biến trên khoảng xác định của nó.
Hàm số (III): y’ = 3x2 – 3.
y’ = 0 <=> 3x2 – 3 = 0 <=> x = ±1 nên hàm số không đồng biến trên khoảng xác định của nó.
Phương pháp giải
Dựa vào tính đơn điệu của hàm số: Cho hàm số y = f(x) xác định trên K. Khi đó:
Hàm số nghịch biến trên K ⇔ f'(x) ≤ 0, ∀ x ∈ K
Hàm số đồng biến trên K ⇔ f'(x) ≥ 0, ∀ x ∈ K
Ghi nhớ: f'(x) = 0 chỉ tại một số hữu hạn điểm hoặc vô hạn điểm rời rạc trên K.
Chú ý:
Nếu đồ thị hàm f'(x) nằm bên dưới Ox trên khoảng K ⇒ f'(x) < 0; ∀ x ∈ K nên hàm f(x) nghịch biến trên K.
Nếu đồ thị hàm f'(x) nằm bên trên Ox trên khoảng K ⇒ f'(x) > 0; ∀ x ∈ K nên hàm f(x) đồng biến trên K.
Xem thêm một số kiến thức liên quan:
Lý thuyết Tính đơn điệu và cực trị của hàm số (Kết nối tri thức) | Lý thuyết Toán 12
Tìm tất cả giá trị của m để hàm số đồng biến trên từng khoảng xác định
Đồ thị của hàm số y = x4 – x2 + 1 có bao nhiêu điểm cực trị có tung độ dương?
Trong các hàm số sau, hàm số nào nghịch biến trên các khoảng xác định của chúng
Trong các hàm số sau, hàm số nào nghịch biến trên khoảng (-1;1)?
Cho hàm số y = f(x) có đạo hàm trong khoảng (a, b) chứa điểm x0 (có thể trừ điểm x0). Tìm mệnh đề đúng trong các mệnh đề sau:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
