Cho tam giác ABC vuông ở A và BC = 2.AB. Gọi E là trung điểm của BC. Tia phân giác của góc B cắt AC tại D....

Question

Cho tam giác ABC vuông ở A và BC = 2.AB. Gọi E là trung điểm của BC. Tia phân giác của góc B cắt AC tại D. a) Chứng minh DB là phân giác của góc ADE. b) Chứng minh BD = DC.

VietJack · Accepted Answer

a) Vì BC = 2 AB Mà E là trung điểm của BC => AB = BE = EC Xét ΔABD và ΔEBD có: AB = BE (cmt) góc A1 = góc A2(gt) BD: cạnh chung => ΔABD = ΔEBD (c.g.c) => góc ADB = góc EDB => DB là tia phân giác của góc ADE b) VÌ ΔABD = ΔEBD( cmt) => góc BAD = góc BED = 90 Mà : góc DEB + góc DEC =180 => góc DEB = góc DEC Xét ΔDEB và ΔDEC có: DE: cạnh chung góc DEB = góc DEC(cmt) BE = CE(gt) => ΔDEB = ΔDEC(c.g.c) => BD = DC Phương pháp giải: Các trường hợp bằng nhau của tam giác a. Trường hợp bằng nhau thứ nhất của tam giác cạnh – cạnh – cạnh (c.c.c) Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau. Xét 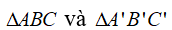có: AB = A’B’ AC = A’C’ BC = B’C’ thì b. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c) Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau c. Trường hợp bằng nhau thứ ba của hai tam giác: góc – cạnh – góc Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau. Các trường hợp bằng nhau của tam giác vuông • Hai cạnh góc vuông Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (cạnh – góc – cạnh ) • Cạnh góc vuông và góc nhọn kề cạnh đó Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc ) • Cạnh huyền – góc nhọn Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc) • Cạnh huyền – cạnh góc vuông Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. Ví dụ: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC. Chứng minh rằng

Câu hỏi:

Cho tam giác ABC vuông ở A và BC = 2.AB. Gọi E là trung điểm của BC. Tia phân giác của góc B cắt AC tại D.

a) Chứng minh DB là phân giác của góc ADE.

b) Chứng minh BD = DC.

Trả lời:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Dấu 3 chấm dọc trong phép tính nghĩa là gì?

Câu 2:

Cho $S =$ $\frac{1}{7^{2}}$ $+$ $\frac{2}{7^{3}}$ $+$ $...$ $+$ $\frac{69}{7^{70}}$ Chứng tỏ $S < \frac{1}{36}$

Câu 3:

Cho hình thang vuông ABCD, góc A = góc D = 90^o và AD = DC (AB<CD). F là giao điểm của DA và CB.

Chứng minh: $\frac{1}{A D^{2}} = \frac{1}{B C^{2}} + \frac{1}{E C^{2}}$

Câu 4:

Câu 5:

Chứng minh hằng đẳng thức : $a^{3} - b^{3} = (a - b) (a^{2} + a b + b^{2})$

Câu 6:

Lũy thừa và bội số trong toán 6

Câu 7:

Hai tia trùng nhau là gì?

Hai tia đối nhau là gì?

Câu 8:

Cho Tanx= $\frac{1}{2}$ . Tính giá trị của biểu thức: A = $\frac{2 S i n 2 x}{2 - 3 C o s 2 x}$

Câu 9:

Câu 10:

Chứng minh rằng: Với mọi số tự nhiên n thì : $n^{2} + n + 2$ không chia hết cho 5

Câu 11:

3 lọ mực đỏ và 2 lọ mực xanh giá 23000 đồng. 2 lọ mực đỏ và 3 lọ mực xanh giá 22000 đồng. Tìm giá tiền 1 lọ mực mỗi loại.

Câu 12:

Một số chính phương chia cho 3 thì số dư có thể bằng bao nhiêu?

Câu 13:

Tìm x, y biết: $x y + 3 x + y = 5$

Câu 14:

Tính: $- 60 + 2^{2} . [(- 35 + 5^{3} . 3) : (- 8) - 15]$

Đề thi liên quan

Câu hỏi mới nhất