Với tóm tắt lý thuyết Toán lớp 11 Bài 1: Dãy số sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 11.

Lý thuyết Toán lớp 11 Bài 1: Dãy số

A. Lý thuyết Dãy số

I. Khái niệm

• Dãy số hữu hạn

Mỗi hàm số u: $\left\{1;2;3;...;m\right\}\to \mathbb{R}\left(m\in {\mathbb{N}}^{\ast }\right)$ được gọi là một dãy số hữu hạn.

Do mỗi số nguyên dương $k\left(1\le k\le m\right)$ tương ứng với đúng một số $u_k$ nên ta có thể viết dãy số đó dưới dạng khai triển: $u_1,u_2,u_3,...,u_m$

Số $u_1$ là số hạng đầu; $u_m$ là số hạng cuối cùng của dãy số đó.

• Dãy số vô hạn

Mỗi hàm số u: ${\mathbb{N}}^{\ast }\to \mathbb{R}$ được gọi là một dãy số vô hạn.

Do mỗi số nguyên dương $n$ tương ứng với đúng một số $u_n$ nên ta có thể viết dãy số đó dưới dạng khai triển: $u_1,u_2,u_3,...,u_n,...$

Số $u_1$ là số hạng đầu; $u_n$ là số hạng thứ n và gọi là số hạng tổng quát của dãy số.

2. Cách cho một dãy số

* Một dãy số có thể cho bằng:

Liệt kê các số hạng (chỉ dùng cho các dãy hữu hạn và có ít số hạng).

Công thức của số hạng tổng quát.

Diễn đạt bằng lời cách xác định mỗi số hạn tổng quát của dãy số đó.

Phương pháp truy hồi.

3. Dãy số tăng, dãy số giảm

Dãy số $\left(u_n\right)$ được gọi là dãy số tăng nếu ta có $u_{n+1}>u_n$$,\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

Dãy số $\left(u_n\right)$ được gọi là dãy số giảm nếu ta có $u_{n+1}<u_n$$,\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

4. Dãy số bị chặn

Dãy số $\left(u_n\right)$ được gọi là bị chặn trên nếu $\mathrm{\exists }$ số M sao cho $u_n\le M,$ $\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

Dãy số $\left(u_n\right)$ được gọi là bị chặn dưới nếu $\mathrm{\exists }$ số m sao cho $u_n\ge m,$ $\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

Dãy số $\left(u_n\right)$ được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m, M sao cho $m\le u_n\le M,$$\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

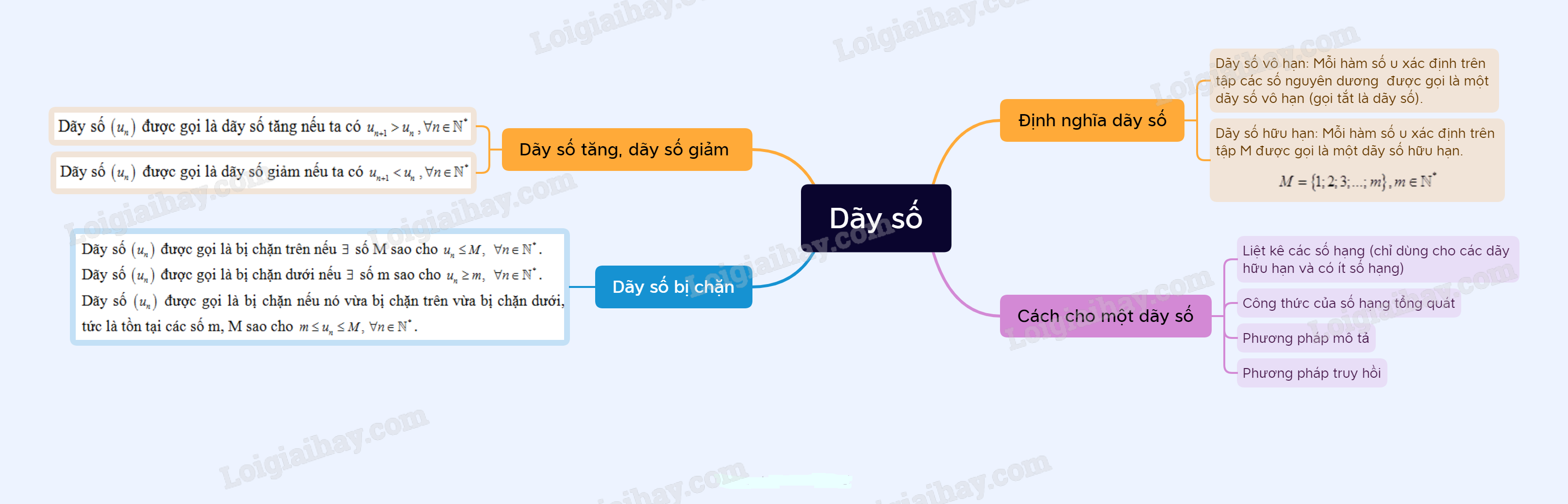
Sơ đồ tư duy Dãy số.

B. Bài tập Dãy số

Bài 1. Cho dãy số (u_n) với u_n = (–1)ⁿ.2n.

a) Hãy viết 6 số hạng đầu của dãy;

b) Viết dạng khai triển của dãy.

Hướng dẫn giải

a) Sáu số hạng đầu của dãy là:

u₁ = –2; u₂ = 4; u₃ = –6; u₄ = 8; u₅ = –10; u₆ = 12.

b) Dạng khai triển của dãy (u_n) là: –2, 4, –6, 8, …., (–1)ⁿ.2n, ….

Bài 2. Chứng minh rằng dãy số (u_n) với $u_n=\frac{4}{3}-n^2$ là dãy số giảm và bị chặn trên.

Hướng dẫn giải

Vì n ∈ ℕ* nên 2n + 1 ≥ 3

Suy ra  –(2n + 1) ≤ –3 < 0

Do đó u_n+1 < u_n, suy ra dãy số là dãy số giảm.

• Vì n² ≥ 1 với mọi n ∈ ℕ* nên –n² ≤ –1

Suy ra $\frac{4}{3}-n^2\le \frac{1}{3}$

Hay $u_n\le \frac{1}{3}$ với mọi n ∈ ℕ*.

Do đó dãy số (u_n) là dãy số bị chặn trên.

Bài 3. Hãy nêu cách xác định mỗi dãy số sau:

a) Cho dãy số (u_n) với u_n là các số chính phương được sắp xếp từ bé đến lớn (1)

b) Cho dãy số (u_n) với $u_n=\frac{2n}{n^2+1}$(2)

c)  Cho dãy số (u_n) với  u₁ = –1, u_n = 2u_{n – 1} + 3 (với n > 1) (3)

Hướng dẫn giải

a) Dãy số (1) được xác định bằng cách diễn đạt bằng lời cách xác định mỗi số hạng của dãy số.

b) Dãy số (2) được xác định bằng cách cho công thức của số hạng tổng quát của dãy số.

c) Dãy (3) được xác định bằng phương pháp truy hồi.

Xem thêm các bài tóm tắt lý thuyết Toán lớp 11 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 4: Phương trình lượng giác cơ bản

Lý thuyết Bài 1: Dãy số

Lý thuyết Bài 2: Cấp số cộng

Lý thuyết Bài 3: Cấp số nhân

Lý thuyết Bài 1: Giới hạn của dãy số

Lý thuyết Bài 2: Giới hạn của hàm số

Xem thêm các bài tóm tắt lý thuyết chương Toán lớp 11 Cánh diều hay, chi tiết khác:

Lý thuyết Chương 1: Hàm số lượng giác và phương trình lượng giác

Lý thuyết Chương 2: Dãy số. Cấp số cộng. Cấp số nhân

Lý thuyết Chương 3: Giới hạn. Hàm số liên tục

Lý thuyết Chương 4: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song