Với giải Hoạt động 1 trang 114 Toán 11 Tập 1 Cánh diều chi tiết trong Bài 6: Phép chiếu song song. Hình biểu diễn của một hình không gian giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải bài tập Toán lớp 11 Bài 6: Phép chiếu song song. Hình biểu diễn của một hình không gian

Hoạt động 1 trang 114 Toán 11 Tập 1: Cho mặt phẳng (P) và đường thẳng ℓ cắt mặt phẳng (P). Qua mỗi điểm M trong không gian, có bao nhiêu đường thẳng song song hoặc trùng với đường thẳng ℓ? Đường thẳng đó và mặt phẳng (P) có bao nhiêu điểm chung? (Hình 76)

Lời giải:

Qua mỗi điểm M trong không gian, có duy nhất một đường thẳng song song hoặc trùng với đường thẳng ℓ. Đường thẳng đó và mặt phẳng (P) có 1 điểm chung.

Lý thuyết Phép chiếu song song

1. Định nghĩa

Cho mặt phẳng $\left(P\right)$và đường thẳng $l$ cắt $\left(P\right)$. Phép đặt tương ứng mỗi điểm M trong không gian với điểm M’ của mặt phẳng $\left(P\right)$ sao cho MM’ song song hoặc trùng với $l$ được gọi là phép chiếu song song lên mặt phẳng $\left(P\right)$ theo phương $l$.

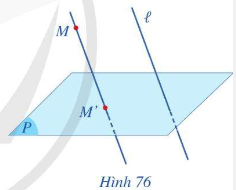
Mặt phẳng $\left(P\right)$ gọi là mặt phẳng chiếu, đường thẳng  $l$ gọi là phương chiếu, điểm M’ gọi là hình chiếu song song (hoặc ảnh) của điểm M qua phép chiều song song.

2. Tính chất

- Phép chiếu song song biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và không làm thay đổi thứ tự 3 điểm đó.

- Phép chiếu song song biến đường thẳng thành đường thẳng, tia thành tia, đoạn thẳng thành đoạn thẳng.

- Phép chiếu song song biến 2 đường thẳng song song thành 2 đường thẳng song song hoặc trùng nhau.

- Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng cùng nằm trên một đường thẳng hoặc nằm trên hai đường thẳng song song.