Với giải Bài 5 trang 104 sách bài tập Toán lớp 6 Chân trời sáng tạo chi tiết trong Bài 7: Số đo góc. Các góc đặc biệt giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:
Giải SBT Toán lớp 6 Bài 7: Số đo góc. Các góc đặc biệt
Bài 5 trang 104 sách bài tập Toán lớp 6 Tập 2: Vẽ ba đoạn thẳng AB, MN và PQ cùng có trung điểm I.
Lời giải:
Ba đoạn thẳng AB, MN và PQ cùng có trung điểm I nên:
IA = IB = AB : 2;
IM = IN = MN : 2;
IP = IQ = PQ : 2.
Ta có thể vẽ hình theo hai cách sau:
Cách 1: Tất cả các điểm đều nằm trên một đường thẳng hay cả ba đoạn thẳng trên một đường thẳng.
Ba đoạn thẳng AB, MN và PQ cùng có trung điểm I nên độ dài của ba đoạn thẳng này khác nhau (vì nếu bằng nhau thì ba đoạn thẳng này trùng nhau).
Chẳng hạn: AB > PQ > MN.
- Vẽ một đường thẳng bất kỳ, lấy điểm I thuộc đường thẳng này.
- Ta lấy các điểm A, B, P, Q, M, N thuộc đường thẳng này sao cho IA = IB, IP = IQ, IM = IN.
Ta có ba đoạn thẳng AB, MN và PQ cùng có trung điểm I như hình vẽ:

Cách 2: Tất cả các điểm không cùng nằm trên một đường thẳng hay ba đoạn thẳng không cùng nằm trên một đường thẳng.
Cách vẽ:
- Lấy điểm I bất kì.
- Qua I vẽ ba đường thẳng phân biệt (không có đường thẳng nào trùng nhau)
- Trên đường thẳng thứ nhất, lấy điểm A và B khác phía với điểm I sao cho IA = IB.
- Trên đường thẳng thứ hai, lấy điểm M và N khác phía với điểm I sao cho IM = IN.
- Trên đường thẳng thứ ba, lấy điểm P và Q khác phía so với điểm I sao cho IP = IQ.
Ta có ba đoạn thẳng AB, MN và PQ cùng có trung điểm I như hình vẽ:
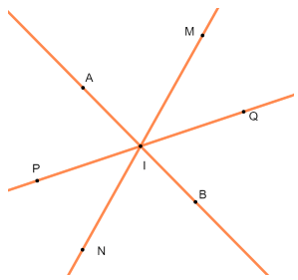
Xem thêm lời giải SBT Toán lớp 6 Chân trời sáng tạo hay, chi tiết khác:
Bài 4 trang 103 sách bài tập Toán lớp 6 Tập 2: Hãy vẽ các đoạn thẳng có độ dài:...
Bài 5 trang 104 sách bài tập Toán lớp 6 Tập 2: Vẽ ba đoạn thẳng AB, MN và PQ cùng có trung điểm I...