1. Định nghĩa

Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.

Tổng quát: ABCD là hình vuông ⇔

Nhận xét:

+ Hình vuông là hình chữ nhật có bốn cạnh bằng nhau.

+ Hình vuông là hình thoi có bốn góc vuông.

+ Hình vuông vừa là hình chữ nhật vừa là hình thoi.

2. Tính chất

Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.

3. Dấu hiệu nhận biết hình vuông

+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

+ Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.

+ Hình thoi có một góc vuông là hình vuông.

+ Hình thoi có hai đường chéo bằng nhau là hình vuông.

4. Công thức tính chu vi hình vuông

Chu vi là độ dài đường bao quanh một hình hai chiều.

Chu vi hình vuông là tổng độ dài của bốn cạnh của hình vuông đó; hoặc chu vi hình vuông bằng 4 lần độ dài của một cạnh hình vuông.

Công thức tính chu vi hình vuông:

P = a x 4

Trong đó: 

• P: Chu vi

• a: độ dài một cạnh bất kỳ

Ví dụ: Tính chu vi hình vuông có cạnh 4cm.

Đáp án:

Chu vi hình vuông là: P = 4 . 4 = 16 cm2

5. Công thức tính diện tích hình vuông

Diện tích hình vuông được đo bằng độ lớn của bề mặt hình, là phần mặt phẳng ta có thể nhìn thấy của hình vuông. 

Diện tích hình vuông bằng bình phương chiều dài cạnh hình vuông.

Công thức tính diện tích hình vuông:

S = a x a = a2

Trong đó:

• S: diện tích 

• a: chiều dài các cạnh hình vuông

6. Bài tập liên quan đến hình vuông

Ví dụ 1: Cho hình bên, tứ giác AEDF là hình gì? Vì sao?

Đáp án:

Tứ giác AEDF là hình vuông, vì:

Theo hình vẽ, góc A = góc E = góc F = 90°

Tứ giác có ba góc vuông nên nó là hình chữ nhật (DHNB).

Xét hình chữ nhật AEDF có AD là đường phân giác của góc A (góc FAE = góc EAD = 45°)

⇒ AEDF là hình vuống (DHNB)

Ví dụ 2: Hình chữ nhật ABCD có AB = 2AD. Gọi E, F lần lượt là trung điểm của AB và CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.

a. ADFE là hình gì?

b. MENF là hình gì?

Đáp án:

a. Gọi AD = a thì AB = 2a

Vì E là trung điểm của AB, F là trung điểm của DC

mà AB = DC, AB = 2AD

⇒ AE = EB = BC = CF = FD = AD = BC = EF = a

Xét tứ giác ADFE có 4 cạnh bằng nhau là AD = DF = EF = AE = a 

⇒ ADFE là hình thoi

Xét hình thoi ADFE có góc DAE = 90°

⇒ ADFE là hình vuông (DHNB)

b. Tương tự như câu a, ta cũng chứng minh được tứ giác EBCF là hình vuông.

Vì hình vuông AEFD và hình vuông EFCB đều có cạnh là a ⇒ Hai hình vuông này bằng nhau.

Áp dụng tính chất về đường chéo vào hai hình vuông ADFE và MENF, ta được:

AF vuông góc với DE, EC vuông góc với FB ⇒ Góc EMF = góc ENF = 90°

Ta có: góc DEF + góc EDF = 90°

góc FCE + góc CEF = 90°

mà góc EDF = góc ECF (tính chất đường chéo trong hình vuông)

⇒ góc DEF + góc CEF = 90° hay góc MEN = 90°

Xét tứ giác MFNE có góc MEN = góc ENF = góc EMF = 90°

⇒ MFNE là hình chữ nhật (DHNB)

Lại có EF là đường phân giác của góc MEN (vì, góc DEF = góc FEC = 45°)

⇒ từ giác MFNE là hình vuông (DHNB)

Ví dụ 3: Hình vuông ABCD. Trên BC lấy M, trên CD lấy N sao cho BM = CN và AM vuông góc BN

Đáp án:

Áp dụng định nghĩa và giả thiết vào hình vuông ABCD, ta có:

AB = BC

góc A = góc B = 90

BM = CN

⇒ tam giác ABM = tam giác BCN (cgc) nên AM = BN

Gọi AM giao BN tại I

- Áp dụng tính chất về góc vào tam giác vuông ABM và BCN kết quả của hai tam giác bằng nhau, ta có:

góc BAM + góc AMB = 90°

góc BAM = góc NBC 

⇒ góc AMB + góc NBC = 90° (1)

Áp dụng tính chất về góc vào tam giác BIM ta có:

góc IBM + góc BIM + góc IMB = 180° (2)

Từ (1) và (2) ⇒ góc BIM = 180° - 90° = 90° hay AM vuông góc BN

Ví dụ 4: Hình vuông ABCD. Trên BC lấy M, qua A kẻ AN vuông góc AM (N thuộc tia đối của tia DC). Gọi I là trung điểm của MN. Chứng minh:

a. AM = AN

b. B, I, D thẳng hàng

Đáp án:

a. Áp dụng định nghĩa và giả thiết vào hình vuông ABCD, ta được:

góc DAB = góc ABC = góc CDA

góc A1 + góc A2 = góc A2 + góc A3 = góc DAB = 90° => góc A1 = góc A3

AB = AD

- Xét tam giác ABM và tam giác ADN có

góc B = góc D = 90°

AB = AD

góc A1 = góc A3

=> tam giác ABM = tam giác ADN (gcg)

=> AM = AN

b. Nối IA, IC thì IA và IC lần lượt là các đường trung tuyến ứng với cnahj huyền của hai tam giác vuông AMN, CMN.

Áp dụng tính chất đường trung tuyến với cạnh dhueenf vào hai tam giác vuông trên và định nghĩa hình vông ta được:

IA = IC = 1/2 MN

BA = BC

Điều nàu chứng tỏ hai điểm B và I cách đều hai điểm A và C nên BI là đường trung trực của đoạn AC.

Mặt khác theo tính chất về đường chéo của hình vuông thì BD là trung trực của AC mà đoạn AC thì chỉ có một đường trung trực nên BI trùng với BD hay B, I, D thẳng hàng. 

Ví dụ 5: Cho tam giác ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và F

a. AEDF là hình gì?

b. Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình thoi?

c. Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì? Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình vuông?

Đáp án:

a. Tứ giác AEDF là hình bình hành

Giải thích: Từ giả thiết: DE//AC và DF // AB

⇒ DE // AF và DF // AE

Tứ giác AEDF có các cạnh đối song song nên nó là hình bình hành

b. Giả sử AEDF là hình thoi khi đó theo tính chất vẽ đường chéo của hình thoi thì AD là đường phân giác của góc A.

Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì tứ giác AEDF là hình thoi

c. Nếu tam giác ABC vuông tại A thì hình bình hành AEDF là hình chữ nhật. Nếu tam giác ABC vuông tại A và D là giao điểm của tia phân giác góc A với BC thì AEDF vừa là chữ nhật vừa là hình thoi nên nó là hình vuông.

Ví dụ 6: Cho hình vuông ABCD. Gọi I,K lần lượt là trung điểm của AD và DC.

a) Chứng minh rằng BI ⊥ AK.

b) Gọi E là giao điểm của BI và AK. Chứng minh rằng CE = AB.

Đáp án:

Xét Δ BAI và Δ ADK có:

⇒ Δ BAI = Δ ADK ( c - g - c )

⇒ ABIˆ = DAKˆ (góc tương ứng bằng nhau)

Mà IAEˆ + EABˆ = 90⁰ ⇒ ABIˆ + EABˆ = 90⁰

+ Xét Δ ABE có EABˆ + ABEˆ + AEBˆ = 180⁰

⇒ AEBˆ = 180⁰ - ( ABEˆ + BAEˆ ) = 180⁰ - 90⁰ = 90⁰ hay AK ⊥ BI (đpcm)

+ Xét tứ giác EBCK có KEBˆ + EBCˆ + BCKˆ+ CKEˆ = 360⁰

⇒ EBCˆ + EKCˆ = 180⁰.

Mà AKDˆ + AKCˆ = 180⁰ nên EBCˆ = EKDˆ

+ Tứ giác EBCK nội tiếp nên BECˆ = BKCˆ

Mà BKCˆ = AKDˆ nên EBCˆ = BECˆ hay tam giác BEC cân tại C

⇒ CE = BC = AB (đpcm)

Ví dụ 7: Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm M, N sao cho MANˆ = 45⁰. Trên tia đối của của tia DC lấy điểm K sao cho DK = BM. Hãy tính :

a) Tính số đo KANˆ = ?

b) Chu vi tam giác MCN theo a.

Đáp án:

a) Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được

⇒ Δ ABM = Δ ADK ( c - g - c )

Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:

 ⇒ KANˆ = A₃ˆ + A₄ˆ = A₁ˆ + A₃ˆ = 90⁰ - 45⁰ = 45⁰

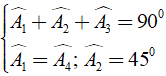
b) Đặt BM = DK = x thì KN = x + DN, MC = a - x, CN = a - DN

Từ kết quả của hai tam giác bằng nhau ở câu a và giả thiết ta có:

 ⇒ Δ AMN = Δ AKN ( c - g - c )

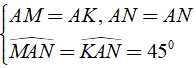
⇒ MN = KN (cạnh tương ứng bằng nhau)

Khi đó, chu vi của tam giác MCN là

MC + CN + MN = a - x + a - DN + x + DN = 2a.