Phương trình đường thẳng đi qua 2 điểm chi tiết, đầy đủ 2024

ttinhin Ngày: 10-09-2024 Lớp 10

3.2 K

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Phương trình đường thẳng đi qua 2 điểm lớp 10, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Phương trình đường thẳng đi qua 2 điểm

1. Phương trình tổng quát của đường thẳng

Đường thẳng Δ có phương trình tổng quát là: $ax + by + c = 0;\left( {{a^2} + {b^2} \ne 0} \right)$ nhận $\overrightarrow n = \left( {a;b} \right)$ làm vectơ pháp tuyến.

2. Phương trình tham số của đường thẳng

- Phương trình tham số của đường thẳng đi qua điểm $A\left( {{x_0},{y_0}} \right)$ nhận $\overrightarrow u (a,b)$ làm vecto chỉ phương, Ta có:

$B\left( {x,y} \right) \in d \Leftrightarrow \overrightarrow {AB} = t\overrightarrow u \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x - {x_0} = at} \\ {y - {y_0} = bt} \end{array}} \right.$

$\Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x = {x_0} + at} \\ {y = {y_0} + bt} \end{array}} \right.;\left( {{a^2} + {b^2} \ne 0,t \in \mathbb{R}} \right)$

- Đường thẳng d đi qua điểm $A\left( {{x_0},{y_0}} \right)$ , nhận $\overrightarrow u (a,b)$ là vecto chỉ phương, phương trình chính tắc của đường thẳng là $\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b}$ với $(a,b \ne 0)$

3. Cách viết phương trình đường thẳng đi qua hai điểm

a. Sử dụng định nghĩa

Bài toán: Cho hai điểm A(a, b), B(c, d). Viết phương trình tổng quát của đường thẳng d đi qua hai điểm A và B.

Phương pháp:

Bước 1: Tính: $\overrightarrow {AB} = \left( {c - a;d - b} \right)$ (vectơ chỉ phương của đường thẳng d)

Bước 2: Xác định vectơ pháp tuyến của đường thẳng d: $\overrightarrow n = \left( {b - d;c - a} \right)$

Bước 3: Phương trình đường thẳng d:

$\left( {b - d} \right)\left( {x - a} \right) + \left( {c - a} \right)\left( {y - b} \right) = 0$

b. Sử dụng phương trình tổng quát

Bài toán: Cho hai điểm A(a, b), B(c, d). Viết phương trình tổng quát của đường thẳng d đi qua hai điểm A và B.

Phương pháp:

Bước 1: Gọi phương trình tổng quát của đường thẳng d là y = mx + n (*)

Bước 2: Thay tọa độ A, B vào phương trình tổng quát ta thu được hệ phương trình ẩn m, n

$\left\{ {\begin{array}{*{20}{c}} {b = am + n} \\ {d = cm + n} \end{array}} \right. \Rightarrow \left( {m;n} \right) = \left( {?;?} \right)$

Thay m, n vừa tìm được vào phương trình (*) ta suy ra phương trình cần tìm.

4. Bài tập ví dụ minh hoạ

Ví dụ 1: Viết phương trình đường thẳng đi qua các điểm cực trị của hàm số y = x³ - 2x² - x + 1

Lời giải:

Ta có y' = 3x² - 4x - 1, y' = 0 có hai nghiệm phân biệt nên hàm số luôn có 2 điểm cực trị

Thực hiện phép chia y cho y' ta được Viết phương trình đường thẳng đi qua 2 điểm cực trị cực hay, có lời giải

Do đó đường thẳng đi qua hai điểm cực trị có phương trình Viết phương trình đường thẳng đi qua 2 điểm cực trị cực hay, có lời giải

Ví dụ 2: Biết đồ thị hàm số y = x³ - 3mx² + 3(m² - 1)x - m³ có hai điểm cực trị A và B. Viết phương trình đường thẳng AB.

Lời giải:

Thực hiện phép chia y cho y' ta được phương trình đường thẳng đi qua hai điểm cực trị A và B là

AB: y = (-m² + 6m - 9)x - m² + 3m - 3

Ví dụ 3: Tìm m để đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = 2x³ + 3(m - 1)x² + 6(m - 2)x - 1 song song với đường thẳng y = -4x + 1.

Lời giải:

Ta có y' = 6x² + 6(m - 1)x + 6(m - 2)

Hàm số có cực trị ⇔ y' = 0 có 2 nghiệm phân biệt

⇔ Δ' > 0 ⇔ 9(m - 1)² - 36(m - 2) > 0 ⇔ 9(m - 3)² > 0 ⇔ m ≠ 3

Thực hiện phép chia y cho y' ta có phương trình đường thẳng đi qua 2 điểm cực trị là:

d: y = (-m² + 6m - 9)x - m² + 3m - 3

Khi đó d song song với đường thẳng y = -4x + 1

Viết phương trình đường thẳng đi qua 2 điểm cực trị cực hay, có lời giải

Ví dụ 4: Tìm m để đồ thị hàm số y = x³ - 3x² + mx có hai điểm cực trị Avà B đối xứng nhau qua đường thẳng x - 2y - 5 = 0

Lời giải:

Ta có: y' = 3x² - 6x + m; y' = 0 ⇔ 3x²-6x + m = 0

Hàm số có hai cực trị khi và chỉ khi Δ' = 9 - 3m > 0 ⇔ m < 3(*)

Thực hiện phép chia y cho y', suy ra phương trình AB: Viết phương trình đường thẳng đi qua 2 điểm cực trị cực hay, có lời giải

Đường thẳng d: x - 2y - 5 = 0 được viết lại Viết phương trình đường thẳng đi qua 2 điểm cực trị cực hay, có lời giải

Do A,B đối xứng nhau qua dthì thỏa mãn điều kiên cần là 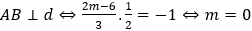Viết phương trình đường thẳng đi qua 2 điểm cực trị cực hay, có lời giải (thỏa mãn (*))

Với m = 0 hàm số có dạng y = x³ - 3x² có hai điểm cực trị A(0;0), B(2;-4)

Khi đó trung điểm AB là I(1;-2) ∈ d (thỏa mãn điều kiện đủ)

Vậy giá trị m = 0 là đáp số của bài toán.

Ví dụ 5: Đường thẳng đi qua A(1; -2) , nhận n→ = (1; -2) làm véc tơ pháp tuyến có phương trình là:

A. x - 2y + 1 = 0.

B. 2x + y = 0

C. x - 2y - 5 = 0

D. x - 2y + 5 = 0

Lời giải:

Gọi (d) là đường thẳng đi qua A và nhận n→ = (1; -2) làm VTPT

=>Phương trình đường thẳng (d) : 1(x - 1) - 2(y + 2) = 0 hay x - 2y – 5 = 0

Chọn C.

Ví dụ 6: Viết phương trình tổng quát của đường thẳng ∆ đi qua M(1; -3) và nhận vectơ n→(1; 2) làm vectơ pháp tuyến.

A. ∆: x + 2y + 5 = 0

B. ∆: x + 2y – 5 = 0

C. ∆: 2x + y + 1 = 0

D. Đáp án khác

Lời giải:

Đường thẳng ∆: qua M( 1; -3) và VTPT n→(1; 2)

Vậy phương trình tổng quát của đường thẳng ∆ là 1(x - 1) + 2(y + 3) = 0

Hay x + 2y + 5 = 0

Chọn A.

Ví dụ 7: Cho đường thẳng (d): x-2y + 1= 0 . Nếu đường thẳng (∆) đi qua M(1; -1) và song song với d thì ∆ có phương trình

A. x - 2y - 3 = 0

B. x - 2y + 5 = 0

C. x - 2y +3 = 0

D. x + 2y + 1 = 0

Lời giải:

Do đường thẳng ∆// d nên đường thẳng ∆ có dạng x - 2y + c = 0 (c ≠ 1)

Ta lại có M(1; -1) ∈ (∆) ⇒ 1 - 2(-1) + c = 0 ⇔ c = -3

Vậy phương trình ∆: x - 2y - 3 = 0

Chọn A

Ví dụ 8: Cho ba điểm A(1; -2); B(5; -4) và C(-1;4) . Đường cao AA’ của tam giác ABC có phương trình

A. 3x - 4y + 8 = 0

B. 3x – 4y - 11 = 0

C. -6x + 8y + 11 = 0

D. 8x + 6y + 13 = 0

Lời giải:

Ta có BC→ = (-6; 8)

Gọi AA’ là đường cao của tam giác ABC

⇒ AA' nhận VTPT n→ = BC→ = (-6; 8) và qua A(1; -2)

Suy ra phương trình AA’: -6(x - 1) + 8(y + 2) = 0

Hay -6x + 8y + 22 = 0 ⇔ 3x - 4y - 11 = 0.

Chọn B

Ví dụ 9: Đường thẳng d đi qua điểm A( 1; -3) và có vectơ pháp tuyến n→( 1; 5) có phương trình tổng quát là:

A. d: x + 5y + 2 = 0

B. d: x- 5y + 2 = 0

C. x + 5y + 14 = 0

D. d: x - 5y + 7 = 0

Lời giải:

Ta có: đường thẳng d: qua A( 1; -3) và VTPT n→( 1; 5)

⇒ Phương trình tổng quát của đường thẳng d:

1( x - 1) + 5.(y + 3) = 0 hay x + 5y + 14 = 0

Chọn C.

Ví dụ 10: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(2; -1); B( 4; 5) và C( -3; 2) . Lập phương trình đường cao của tam giác ABC kẻ từ A

A. 7x + 3y – 11 = 0

B. -3x + 7y + 5 = 0

C. 3x + 7y + 2 = 0

D. 7x + 3y + 15 = 0

Lời giải:

Gọi H là chân đường vuông góc kẻ từ A.

Đường thẳng AH : qua A( 2;-1) và Nhận VTPT BC→( 7; 3)

⇒ Phương trình đường cao AH :

7( x - 2) + 3(y + 1) = 0 hay 7x + 3y – 11 = 0

Chọn A.

Ví dụ 11: Cho tam giác ABC cân tại A có A(1 ; -2). Gọi M là trung điểm của BC và

M( -2 ; 1). Lập phương trình đường thẳng BC ?

A. x + y - 3 = 0

B. 2x - y + 6 = 0

C. x - y + 3 = 0

D. x + y + 1 = 0

Lời giải:

+ Do tam giác ABC cân tại A nên đường trung tuyến AM đồng thời là đường cao

⇒ AM vuông góc BC.

⇒ Đường thẳng BC nhận AM→( -3 ; 3) = -3(1 ; -1) làm VTPT

+ Đường thẳng BC : qua M(-2; 1) và VTPT n→( 1; -1)

⇒ Phương trình đường thẳng BC :

1(x + 2) - 1(y - 1) = 0 hay x - y + 3 = 0

Chọn C.

Ví dụ 12: Cho tam giác ABC có đường cao BH : x + y - 2 = 0, đường cao CK : 2x + 3y - 5 = 0 và phương trình cạnh BC : 2x - y + 2 = 0. Lập phương trình đường cao kẻ từ A của tam giác ABC ?

A. x - 3y + 1 = 0

B. x + 4y - 5 = 0

C. x + 2y - 3 =0

D. 2x - y + 1 = 0

Lời giải:

+ Gọi ba đường cao của tam giác ABC đồng quy tại P. Tọa độ của P là nghiệm hệ phương trình :

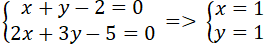
Cách viết phương trình tổng quát của đường thẳng lớp 10 cực hay - Toán lớp 10 ⇒ P( 1 ; 1)

+Tọa độ điểm B là nghiệm hệ phương trình :

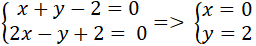
Cách viết phương trình tổng quát của đường thẳng lớp 10 cực hay - Toán lớp 10 ⇒ B( 0 ;2)

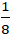
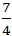
Tương tự ta tìm được tọa độ C(- Cách viết phương trình tổng quát của đường thẳng lớp 10 cực hay - Toán lớp 10 ; )

+ Đường thẳng AP : Cách viết phương trình tổng quát của đường thẳng lớp 10 cực hay - Toán lớp 10

⇒ Phương trình đường thẳng AP :

1(x - 1) + 2(y - 1) = 0 ⇔ x + 2y - 3 = 0

Chọn C.

Ví dụ 13: Phương trình tổng quát của đường thẳng d đi qua O và song song với đường thẳng ∆ : 3x + 5y - 9 = 0 là:

A. 3x + 5y - 7 = 0

B. 3x + 5y = 0

C. 3x - 5y = 0

D. 3x - 5y + 9 = 0

Lời giải:

Do đường thẳng d// ∆ nên đường thẳng d có dạng : 3x + 5y + c = 0 ( c ≠ - 9)

Do điểm O(0; 0) thuộc đường thẳng d nên :

3.0 + 5.0 + c = 0 ⇔ c = 0

Vậy phương trình đường thẳng d: 3x + 5y = 0

Chọn B.

Ví dụ 14: Cho tam giác ABC có B(-2; -4). Gọi I và J lần lượt là trung điểm của AB và AC. Biết đường thẳng IJ có phương trình 2x - 3y + 1 = 0. Lập phương trình đường thẳng BC?

A. 2x + 3y - 1 = 0

B. 2x - 3y - 8 = 0

C. 2x + 3y - 6 = 0

D. 2x - 3y + 1 = 0

Lời giải:

Do I và J lần lượt là trung điểm của AB và AC nên IJ là đường trung bình của tam giác ABC.

⇒ IJ// BC.

⇒ Đường thẳng BC có dạng : 2x - 3y + c = 0 ( c ≠ 1)

Mà điểm B thuộc BC nên: 2.(-2) - 3(-4) + c = 0 ⇔ c = -8

⇒ phương trình đường thẳng BC: 2x - 3y - 8 = 0

Chọn B.

Ví dụ 15: Cho ba đường thẳng (a):3x - 2y + 5 = 0; (b): 2x + 4y - 7 = 0 và

(c): 3x + 4y - 1 = 0 . Phương trình đường thẳng d đi qua giao điểm của a và b , và song song với c là:

A. 24x + 32y - 53 = 0.

B. 23x + 32y + 53 = 0

C. 24x - 33y + 12 = 0.

D. Đáp án khác

Lời giải:

Giao điểm của (a) và ( b) nếu có là nghiệm hệ phương trình :

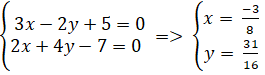
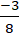
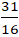
Cách viết phương trình tổng quát của đường thẳng lớp 10 cực hay - Toán lớp 10 ⇒ A( ; )

Ta có đường thẳng d // c nên đường thẳng d có dạng: 3x+ 4y+ c= 0 (c≠-1)

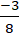
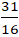
Vì điểm A thuộc đường thẳng d nên : 3. Cách viết phương trình tổng quát của đường thẳng lớp 10 cực hay - Toán lớp 10 + 4. + c = 0 ⇔ c=

Vậy d: 3x + 4y + 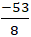Cách viết phương trình tổng quát của đường thẳng lớp 10 cực hay - Toán lớp 10 = 0 ⇔ d₃ = 24x + 32y - 53 = 0

5. Bài tập vận dụng

Câu 1: Trong không gian với hệ tọa độ Oxyz; cho đường thẳng d đi qua A ( -2; 0; 3) và B (1; 1; 5). Tìm mệnh đề sai?

A. Phương trình tham số của d là: Cách viết phương trình đường thẳng đi qua 2 điểm cực hay

B. Phương trình chính tắc của d là: Cách viết phương trình đường thẳng đi qua 2 điểm cực hay

C. Đường thẳng d đi qua điểm H( - 5; -1; 1)

D. Đường thẳng d đi qua điểm K( -11; -3; -3)

Lời giải:

Ta có: Cách viết phương trình đường thẳng đi qua 2 điểm cực hay

Đường thẳng d đi qua A và B nên vectơ chỉ phương của d là u→= Cách viết phương trình đường thẳng đi qua 2 điểm cực hay

Vậy phương trình tham số của d là: Cách viết phương trình đường thẳng đi qua 2 điểm cực hay

Phương trình chính tắc của d là: Cách viết phương trình đường thẳng đi qua 2 điểm cực hay

Cho t= - 1 ta được điểm H( -5; -1; 1) thuộc đường thẳng d.

Cho t= -3 ta được điểm M( -11;- 3; - 3) thuộc đường thẳng d

Chọn A.

Câu 2: Cho đường thẳng d đi qua hai điểm A(1; 2; 0) và B( -2;3; 4). Trong các vecto sau vecto nào là vecto chỉ phương của đường thẳng d

A. ( -3; 1; - 4)

B. ( 6; -2; -8)

C.( 3; -1; -4)

D. (9; -3; -12)

Lời giải:

Ta có: 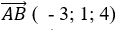Cách viết phương trình đường thẳng đi qua 2 điểm cực hay là một vecto chỉ phương của đường thẳng AB.

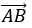
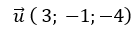
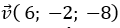
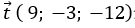
Mà vecto Cách viết phương trình đường thẳng đi qua 2 điểm cực hay cùng phương với các vecto ; và nên ba vecto uX→; v→; t→ cũng là vecto chỉ phương của đường thẳng d

Chọn A.

Câu 3: Viết phương trình chính tắc của đường thẳng Δ biết Δ đi qua A (2; 1; 5) và B (4; -2; 6)?

A. Cách viết phương trình đường thẳng đi qua 2 điểm cực hay

B. Cách viết phương trình đường thẳng đi qua 2 điểm cực hay

C. Cách viết phương trình đường thẳng đi qua 2 điểm cực hay

D. Cách viết phương trình đường thẳng đi qua 2 điểm cực hay

Lời giải:

Vì đường thẳng Δ đi qua 2 điểm A (2; 1; 5) và B (4; - 2; 6) nên có véc tơ chỉ phương là u→=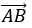 Cách viết phương trình đường thẳng đi qua 2 điểm cực hay =(2; -3 ;1)

Đồng thời đường thẳng Δ đi qua điểm A (2; 1; 5) nên có phương trình là Cách viết phương trình đường thẳng đi qua 2 điểm cực hay

Chọn B.

Câu 4: Cho tam giác ABC có A(2; -1; 3), B(0; 5; 3), C(2; 1; 4). Chọn mệnh đề sai về phương trình đường trung tuyến CN

A. phương trình tham số của CN là: Cách viết phương trình đường thẳng đi qua 2 điểm cực hay

B. Phương trình chính tắc của CN là: Cách viết phương trình đường thẳng đi qua 2 điểm cực hay

C. Phương trình tham số của CN là: Cách viết phương trình đường thẳng đi qua 2 điểm cực hay

D. Phương trình chính tắc của CN là: Cách viết phương trình đường thẳng đi qua 2 điểm cực hay

Lời giải:

Trung điểm A của AB là N(1; 2; 3)

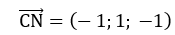
Cách viết phương trình đường thẳng đi qua 2 điểm cực hay =>vectơ chỉ phương của CN là u→ =(1; -1;1)

Vậy phương trình tham số của CN là: Cách viết phương trình đường thẳng đi qua 2 điểm cực hay

Phương trình chính tắc của CN là: Cách viết phương trình đường thẳng đi qua 2 điểm cực hay

Do vecto u→ (-1;1; -1)là vecto chỉ phương của đường thẳng CN nên vecto v→ (-1; 1; -1) cũng là vecto chỉ phương của đường thẳng CN.

=> Đường thẳng CN cũng có phương trình chính tắc là: Cách viết phương trình đường thẳng đi qua 2 điểm cực hay

Chọn D.

Câu 5: Trong không gian với hệ tọa độ Oxyz; phương trình nào sau đây là phương trình chính tắc của đường thẳng đi qua hai điểm O(0; 0;0) và A(-1; 2; -4)?

A. Cách viết phương trình đường thẳng đi qua 2 điểm cực hay