Với Giải Toán lớp 7 trang 103 Tập 2 Cánh diều tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:

Giải Toán 7 trang 103 Tập 2 Cánh diều

Bài 1 trang 103 Toán 7 Tập 2: Trong Hình 94, đường thẳng CD là đường trung trực của đoạn thẳng AB. Chứng minh $\widehat{CA\text{D}}=\widehat{CB\text{D}}$.

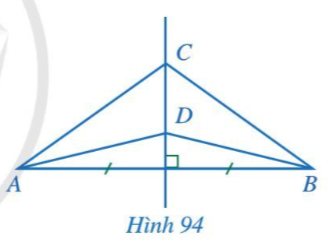
Lời giải:

Chứng minh (Hình vẽ dưới đây):

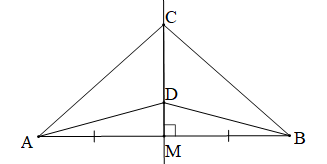
Gọi M là giao điểm của CD và AB. Khi đó M là trung điểm của AB.

CD là đường trung trực của đoạn thẳng AB nên:

+) C thuộc đường trung trực của đoạn thẳng AB do đó CA = CB.

+) D thuộc đường trung trực của đoạn thẳng AB do đó DA = DB.

Xét $∆$CAD và $∆$CBD có:

CD là cạnh chung,

CA = AB (chứng minh trên),

DA = DB (chứng minh trên)

Do đó $∆$CAD = $∆$CBD (c.c.c)

Do đó $\widehat{CA\text{D}}=\widehat{CB\text{D}}$ (hai góc tương ứng)

Vậy $\widehat{CA\text{D}}=\widehat{CB\text{D}}$.

Bài 2 trang 103 Toán 7 Tập 2: Trong Hình 95, đường thẳng a là đường trung trực của cả hai đoạn thẳng AB và CD.

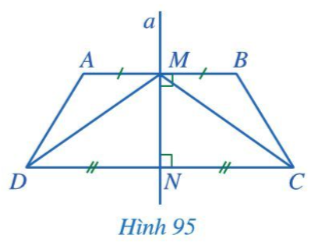
Chứng minh:

a) AB // CD;

b) $∆$MNC = $∆$MND;

c) $\widehat{AMD}=\widehat{BMC}$;

d) AD = BC, $\widehat{A}=\widehat{B}$;

e) $\widehat{A\text{D}C}=\widehat{BC\text{D}}$.

Lời giải:

Chứng minh (Hình 95):

a) Vì a là đường trung trực của cả hai đoạn thẳng AB và CD (giả thiết)

Nên a $\perp$ AB và a $\perp$ CD.

Do đó AB // CD (hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba)

Vậy AB // CD.

b) Ta có: a $\perp$ CD tại N nên $∆$MNC vuông tại N và $∆$MND vuông tại N.

Xét $∆$MNC (vuông tại N) và $∆$MND (vuông tại N) có:

MN là cạnh chung

NC = ND (N là trung điểm của CD).

Do đó $∆$MNC = $∆$MND (hai cạnh góc vuông).

c) Vì $∆$MNC = $∆$MND (chứng minh câu b)

Nên $\widehat{MCN}=\widehat{MDN}$ (hai góc tương ứng). (1)

Do AM // DN nên $\widehat{AM\text{D}}=\widehat{M\text{D}N}$ (hai góc so le trong). (2)

Do BM // CN nên $\widehat{BMC}=\widehat{MCN}$ (hai góc so le trong). (3)

Từ (1), (2) và (3) suy ra $\widehat{AM\text{D}}=\widehat{BMC}$.

Vậy $\widehat{AM\text{D}}=\widehat{BMC}.$

d)Vì $∆$MNC = $∆$MND (chứng minh câu b)

Nên MC = MD (hai cạnh tương ứng).

Xét $∆$AMD và $∆$BMC có:

AM = BM (M là trung điểm của AB),

$\widehat{AM\text{D}}=\widehat{BMC}$ (chứng minh trên),

MD = MC (chứng minh trên)

Do đó $∆$AMD = $∆$BMC (c.g.c)

Suy ra AD = BC (hai cạnh tương ứng) và $\widehat{MA\text{D}}=\widehat{MBC}$ (hai góc tương ứng).

Vậy AD = BC và $\widehat{A}=\widehat{B}$.

e) Vì $∆$AMD = $∆$BMC (chứng minh câu d)

Nên $\widehat{A\text{D}M}=\widehat{BCM}$ (hai góc tương ứng).

Mà $\widehat{M\text{D}N}=\widehat{MCN}$ (chứng minh câu c)

Do đó $\widehat{ADM}+\widehat{M\text{D}N}=\widehat{BCM}+\widehat{MCN}$ 

Hay $\widehat{A\text{D}C}=\widehat{BC\text{D}}$.

Vậy $\widehat{A\text{D}C}=\widehat{BC\text{D}}$

Bài 3 trang 103 Toán 7 Tập 2: Cho ba điểm A, B, C thẳng hàng, điểm B nằm giữa hai điểm A và C. Gọi a và b lần lượt là đường trung trực của các đoạn thẳng AB và BC. Chứng minh rằng a // b.

Lời giải:

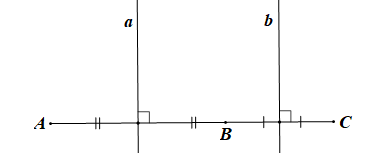
a là đường trung trực của đoạn thẳng AB nên a $\perp$ AB tại trung điểm của AB.

b là đường trung trực của đoạn thẳng BC nên b $\perp$ BC tại trung điểm của BC.

Do A, B, C thẳng hàng và B nằm giữa A và C nên trung điểm của đoạn thẳng AB và trung điểm của đoạn thẳng BC không trùng nhau.

Do đó đường thẳng a và đường thẳng b là hai đường thẳng phân biệt.

Ta có: a $\perp$ AB, b $\perp$ BC, a ≠ b

Do đó a // b.

Vậy a // b.

Bài 4 trang 103 Toán 7 Tập 2: Cho đường thẳng d là đường trung trực của đoạn thẳng AB. Điểm M không thuộc đường thẳng d và đoạn thẳng AB sao cho đường thẳng d cắt đoạn thẳng MB tại điểm I. Chứng minh:

a) MB = AI + IM;

b) MA < MB.

Lời giải:

Chứng minh (Hình vẽ dưới đây):

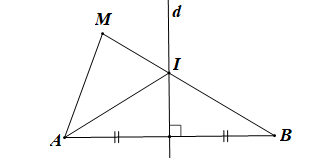
a) Đường thẳng d cắt đoạn thẳng MB tại I nên I thuộc đường trung trực của đoạn thẳng AB.

Do đó AI = BI (tính chất đường trung trực của đoạn thẳng AB)

Khi đó MB = BI + IM = AI + IM.

Vậy MB = AI + IM.

b) Xét trong tam giác AIM có AI + IM > MA (bất đẳng thức trong tam giác)

Mà MB = AI + IM (chứng minh câu a) nên MB > MA.

Vậy MB > MA.

Xem thêm các bài giải Toán lớp 7 Cánh diều hay, chi tiết khác:

Giải Toán 7 trang 100 Tập 2

Giải Toán 7 trang 101 Tập 2

Giải Toán 7 trang 102 Tập 2