Tailieumoi.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 4: Vị trí tương đối của đường thẳng và đường tròn chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 4: Vị trí tương đối của đường thẳng và đường tròn
Sử dụng kiến thức: Cho đường thẳng và đường tròn với là khoảng cách từ đến đường thẳng
+) Nếu thì đường thẳng và đường tròn tiếp xúc nhau.
+) Nếu thì đường thẳng và đường tròn không giao nhau.
Lời giải:
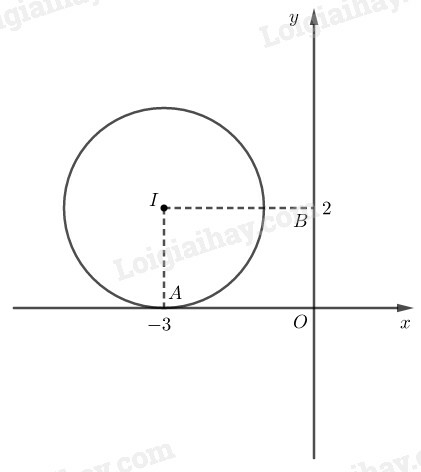
Kẻ
Ta có:
Suy ra đường tròn tiếp xúc với trục hành.
Kẻ
Ta có:
Suy ra đường tròn và trục tung không có điểm chung.
Sử dụng kiến thức:
+) Tập hợp tất cả những điểm cách đều đường thẳng một khoảng cho trước là hai đường thẳng song song với đường thẳng và các một khoảng .
Lời giải:
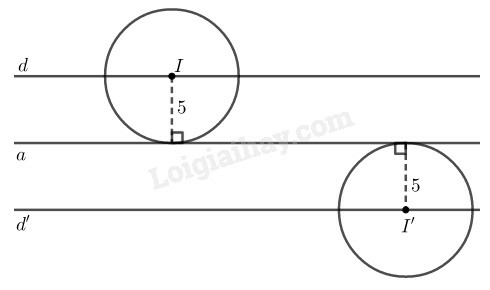
Vì đường tròn tâm bán kính tiếp xúc với đường thẳng nên khoảng cách từ đến là
Vậy nằm trên hai đường thẳng và song song với cách một khoảng bằng
Chứng minh rằng đường tròn có hai giao điểm với đường thẳng
Gọi hai giao điểm nói trên là và Tính độ dài
Phương pháp giải:
Sử dụng kiến thức:
Cho đường thẳng và đường tròn với là khoảng cách từ đến đường thẳng
+) Nếu thì đường thẳng và đường tròn cắt nhau.
Sử dụng định lý Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Lời giải:
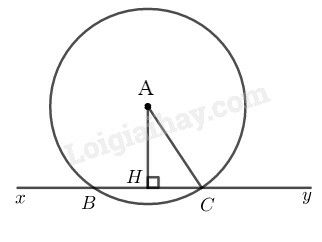
Kẻ
Ta có:
Bán kính đường tròn tâm là nên
Mà
Nên suy ra
Vậy cắt đường thẳng tại hai điểm phân biệt và
Áp dụng định lí Py-ta-go vào tam giác vuông ta có:
Suy ra:
Xét đường tròn tâm A có tại H nên H là trung điểm của BC (đường kính vuông góc với dây thì đi qua trung điểm của dây đó)
Suy ra
Sử dụng định nghĩa, tính chất đường trung bình của tam giác:
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải:
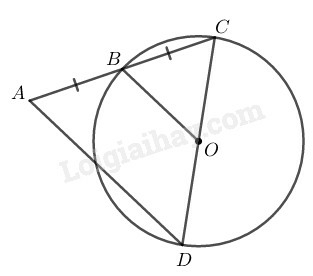
Trong tam giác ta có:
+) là trung điểm của
+) là trung điểm của
Nên là đường trung bình của
Suy ra: ( tính chất đường trung bình của tam giác)
Vậy
Tính độ dài
Chứng minh rằng đường thẳng tiếp xúc với đường tròn có đường kính là
Phương pháp giải:
Sử dung kiến thức:
+) Tứ giác có ba góc vuông là hình chữ nhật.
+) Sử dụng định lí Py-ta-go: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
+) Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy.
+) Nếu thì đường thẳng và đường tròn tiếp xúc nhau (với là khoảng cách từ đến đường thẳng )
Lời giải:
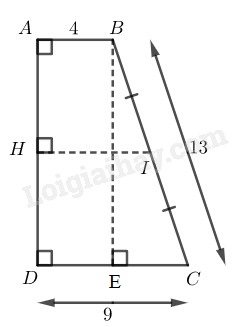
Kẻ tại
Suy ra tứ giác là hình hình chữ nhật (vì có ba góc vuông )
Suy ra ,
Suy ra:
Áp dụng định lí Py-ta-go vào tam giác vuông ta có:
Suy ra:
Vậy:
Gọi là trung điểm của
Ta có:
Kẻ
Xét hình thang ABCD ta có: (cùng vuông góc với AD), mà I là trung điểm BC nên H là trung điểm AD.
Khi đó là đường trung bình của hình thang
Ta có:
Từ và suy ra:
Vậy đường tròn tiếp xúc với đường thẳng
Tứ giác là hình gì Vì sao
Kẻ tiếp tuyến đường tròn tại tiếp tuyến này cắt đường thẳng tại Tính độ dài biết
Phương pháp giải:
Sử dụng kiến thức:
+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
+) Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
Lời giải:
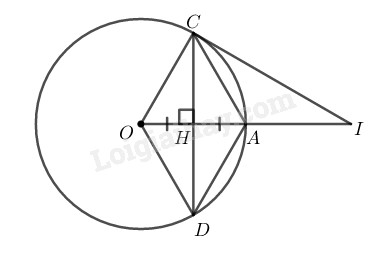
Gọi là giao điểm của và
Vì là đường trung trực của nên:
và
Xét đường tròn (O) có tại H nên H là trung điểm của dây CD hay (đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy)
Vì tứ giác có hai đường chéo CD và OA cắt nhau tại trung điểm H của mỗi đường nên nó là hình bình hành.
Đồng thời nên là hình thoi.
Vì là hình thoi nên
Mà nên , suy ra tam giác đều.
Suy ra: hay
Mà (tính chất tiếp tuyến)
Trong tam giác vuông ta có:
.
là tia phân giác của góc
.
Phương pháp giải:
Sử dụng kiến thức:
+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
+) Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông lên cạnh huyền.
Lời giải:
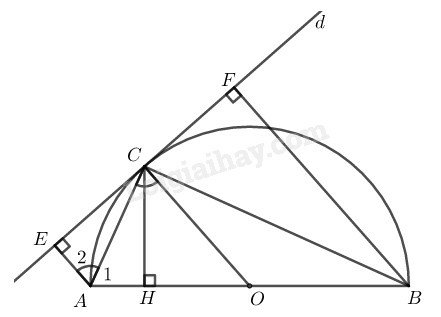
Ta có: ( tính chất tiếp tuyến)
Suy ra:
Mà
Suy ra: (tính chất đường thẳng song cách đều)
Ta có: (theo )
Suy ra: ( hai góc so le trong)
Ta có:
Suy ra: cân tại
Từ và suy ra:
Vậy là tia phân giác của góc hay là tia phân giác của góc
Tam giác nội tiếp trong đường tròn có là đường kính nên
Tam giác vuông tại có
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
Xét hai tam giác và ta có:
+)
+) (tính chất đường phân giác)
+) chung
Suy ra: (cạnh huyền, cạnh góc vuông)
Suy ra:
Xét hai tam giác và ta có:
+)
+)
+) chung
Suy ra: (cạnh huyền, cạnh góc vuông)
Suy ra:
Từ và suy ra:
Bài tập bổ sung (trang 163 SBT Toán 9)
Đường vuông góc với tại ;
Đường vuông góc với tại ;
Hai đường thẳng song song với và cách một khoảng ;
Hai đường thẳng song song với và cách một khoảng
Hãy chọn phương án đúng
Phương pháp giải:
Sử dụng kiến thức: Nếu đường thẳng và đường tròn tiếp xúc với nhau thì , với là khoảng cách từ tâm đường tròn đến đường thẳng
Lời giải:
Vì tiếp xúc với đường tròn nên khoảng cách từ đến đường thẳng bằng bán kính là
Do đó điểm nằm trên hai đường thẳng song song với và cách một khoảng
Chọn
Lời giải:
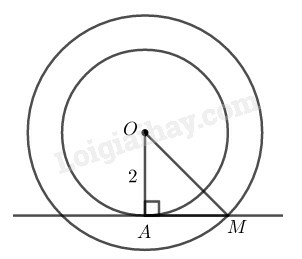
Vì AM là tiếp tuyến của đường tròn (O) nên .
Lại có nên là tam giác vuông cân tại
Theo định lý Pytago ta có:
.
Do điểm cố định nên điểm chuyển động trên đường tròn
Sử dụng kiến thức:
+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
+) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+) Sử dụng định lý Ta-lét.
Lời giải:
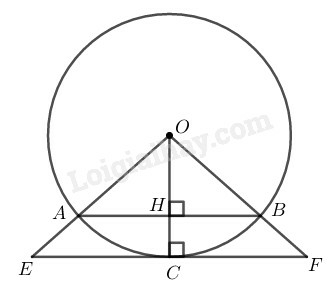
Gọi là tiếp điểm của với đường tròn là giao điểm của và Ta có
(tính chất tiếp tuyến) và (gt) nên tại H.
Xét đường tròn (O) có tại H nên H là trung điểm của AB (đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy)
Suy ra
Xét tam giác OHB vuông tại H, theo định lý Pytago ta có:
Vì nên (định lý Ta-lét)
Vì nên (hệ quả định lý Ta-lét)
Suy ra ,
tức là .