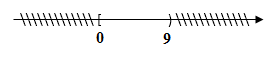Tailieumoi.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 5: Bảng căn bậc hai chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 5: Bảng căn bậc hai
a) ;
b) ;
c) ;
d)
Phương pháp giải:
Sử dụng suy ra hoặc (với ).
Sử dụng bảng căn bậc hai.
Lời giải:
a)
Dùng bảng căn bậc hai ta có:
b)
c)
d)
a) ;
b) ;
c) ;
d) .
Phương pháp giải:
Dùng bảng bình phương để tìm
ÁP dụng: Với
.
Lời giải:
a)
b)
c)
;
d)
.
Lời giải:
Ví dụ: Với câu a) bài 47, ta có:
Tương tự với các câu tiếp theo.
Bài 50 trang 13 SBT Toán 9 tập 1: Thử lại kết quả bài 47 bằng bảng bình phương.Với câu a) bài 47 ta có
Tìm ô có giá trị gần với 15 trong bảng bình phương ta được ô 14,98 và ô 15,05
* Với ô 14,98 tra bảng ta được . Đây là kết quả gần đúng nhưng hơi thiếu.
* Với ô 15,05 tra bảng ta được . Đây là kết quả gần đúng nhưng hơi thừa.
Thực hiện tương tự cho các bài còn lại.
Lời giải:
Sử dụng bảng căn bậc hai, thử lại các kết quả bằng cách tra bảng căn bậc hai cho các kết quả vừa tìm được ở bài 48.
Số là số vô tỉ.
Giả sử không phải là số vô tỉ thì phải tồn tại các số nguyên m và n sao cho trong đó còn hai số và không có ước chung nào khác 1 và (hai số và nguyên tố cùng nhau).
Khi đó, ta có: ... hay (1).
Kết quả (1) chứng tỏ là số chẵn, nghĩa là với là số nguyên.
Thay vào (1) ta được: ... hay (2)
Kết quả (2) chứng tỏ phải là số chẵn.
Hai số và đều là số chẵn, trái với giả thiết và không có ước chung nào khác và .
Vậy là số vô tỉ.
Phương pháp giải:
Áp dụng: Với
.
Lời giải:
Số là số vô tỉ.
Giả sử không phải là số vô tỉ thì phải tồn tại các số nguyên m và n sao cho trong đó còn hai số và không có ước chung nào khác 1 và (hai số và nguyên tố cùng nhau).
Khi đó, ta có: hay (1).
Kết quả (1) chứng tỏ là số chẵn, nghĩa là với là số nguyên.
Thay vào (1) ta được: hay (2)
Kết quả (2) chứng tỏ phải là số chẵn.
Hai số và đều là số chẵn, trái với giả thiết và không có ước chung nào khác và .
Vậy là số vô tỉ.
a) Số là số vô tỉ;
b) Các số ; đều là số vô tỉ.
Lời giải:
a)
Giả sử không phải là số vô tỉ. Khi đó tồn tại các số nguyên và sao cho với . Hai số và không có ước chung nào khác và .
Ta có: hay (1)
Kết quả trên chứng tỏ chia hết cho , nghĩa là ta có với là số nguyên.
Thay vào (1) ta được: hay
Kết quả trên chứng tỏ chia hết cho .
Hai số a và b đều chia hết cho 3, trái với giả thiết và không có ước chung nào khác và .
Vậy là số vô tỉ.
b)
Giả sử là số hữu tỉ, nghĩa là tồn tại số hữu tỉ sao cho
Suy ra: hay là số hữu tỉ.
Điều này vô lí vì là số vô tỉ (theo bài 52 trang 13 SBT toán 9 tập 1)
Vậy là số vô tỉ.
*Giả sử là số hữu tỉ, nghĩa là tồn tại một số hữu tỉ mà:
Suy ra: hay là số hữu tỉ.
Điều này vô lí vì là số vô tỉ (theo bài 52 trang 13 SBT toán 9 tập 1)
Vậy là số vô tỉ.
Áp dụng: Với ta có:
.
Lời giải:
Điều kiện:
Ta có: .
Biểu diễn trên trục số:

và biểu diễn tập hợp đó trên trục số.
Phương pháp giải:
Áp dụng:
Lời giải:
Điều kiện:
Ta có:
Suy ra
Biểu diễn trên trục số: