Với giải Bài 37 trang 24 Toán lớp 9 chi tiết trong Bài 6: Giải bài toán bằng cách lập hệ phương trình (tiếp  theo) giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán lớp 9 Bài 6: Giải bài toán bằng cách lập hệ phương trình (tiếp theo)

Bài 37 trang 24 SGK Toán 9 Tập 2: Hai vật chuyển động đều trên một con đường tròn đường kính 20cm, xuất phát cùng một lúc, từ cùng một điểm. Nếu chuyển động cùng chiều thì cứ 20 giây chúng lại gặp nhau. Nếu chuyển động ngược chiểu thì cứ sau 4 giây chúng lại gặp nhau. Tính vận tốc của mỗi vật.

Lời giải

Gọi vận tốc của vật thứ nhất là x(cm/s), vận tốc của vật thứ hai là y(cm/s)

Giả sử vật thứ nhất đi nhanh hơn vật thứ hai.

Điều kiện x > y > 0.

Chu vi vòng tròn là : 20.π (cm)

Quãng đường vật thứ nhất đi được trong 20s là 20x (cm)

Quãng đường vật thứ hai đi được trong 20s là 20y (cm)

Khi chuyển động cùng chiều, cứ 20 giây chúng lại gặp nhau, nghĩa là quãng đường 2 vật đi được trong 20 giây chênh lệch nhau đúng bằng 1 vòng tròn. Nên ta có phương trình: 20x – 20y = 20π   (1).

Quãng đường vật thứ nhất đi được trong 4s là 4x (cm)

Quãng đường vật thứ hai đi được trong 4s là 4y (cm)

Khi chuyển động ngược chiều, cứ 4 giây chúng lại gặp nhau, nghĩa là tổng quãng đường hai vật đi được trong 4 giây là đúng 1 vòng tròn nên ta có phương trình: 4x + 4y = 20π   (2)

Từ (1) và (2) ta có hệ phương trình:

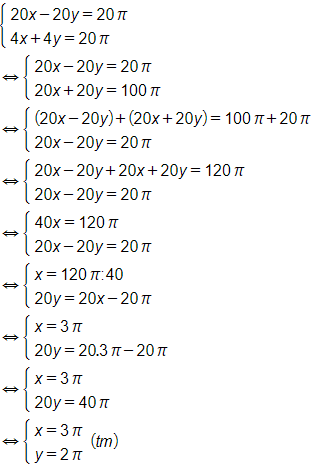
Vậy vận tốc của hai vật lần lượt là $3\mathrm{\pi }$ và $2\mathrm{\pi }$.