$(3+2i)+(5+8i)$;

$(7+5i)–(4+3i)$;

Lời giải:

$(3+2i)+(5+8i)=(3+5)+(2+8)i=8+10i.$

$(7+5i)–(4+3i)=(7–4)+(5–3)i=3+2i.$

Lời giải:

$(3+2i)(2+3i)$ $=3.2+3.3i+2i.2+2i.3i$ $=6+9i+4i–6=13i.$

Lời giải:

* Các tính chất của phép cộng:

- Giao hoán: $z+z^{\prime }=z^{\prime }+z$

- Kết hợp: $z_1+\left(z_2+z_3\right)$ $=\left(z_1+z_2\right)+z_3=z_1+z_2+z_3$

* Các tính chất của phép nhân:

- Giao hoán: $z.z^{\prime }=z^{\prime }.z$

- Kết hợp: $z_1.\left(z_2.z_3\right)$ $=\left(z_1.z_2\right).z_3=z_1.z_2.z_3$

* Tính chất phân phối của phép nhân với phép cộng: $z_1\left(z_2+z_3\right)=z_1{z}_2+z_1{z}_3$

Nêu cách tính $i^n$ với $n$ là một số tự nhiên tuỳ ý.

Lời giải:

$\begin{array}{l}{i}^3=i^2.i=-1.i=-i\\ i^4=i^3.i=-i.i=-i^2=1\\ i^5=i^4.i=1.i=i\end{array}$.

Ta có: 

Với $n=4k$ thì $i^n=i^{4k}={\left(i^4\right)}^k=1^k=1$

Với $n=4k+1$ thì $i^n=i^{4k+1}=i^{4k}.i=1.i=i$

Với $n=4k+2$ thì $i^{4k+2}=i^{4k}.i^2=1.\left(-1\right)=-1$

Với $n=4k+3$ thì $i^{4k+3}=i^{4k}.i^3=1.\left(-i\right)=-i$

Vậy $i^{4k}=1,$ $i^{4k+1}=i,$$i^{4k+2}=-1,$$i^{4k+3}=-i$.

Lý thuyết Bài 2: Cộng, trừ và nhân số phức

Kiến thức cơ bản

$(a+bi)+(c+di)=(a+c)+(b+d)i$;

$(a+bi)-(c+di)=(a-c)+(b-d)i$;

$(a+bi)(c+di)=(ac-bd)+(ad+bc)i$.

Nhận xét

- Phép cộng và phép nhân số phức được thực hiện tương tự như đối với số thực, với chú ý  $i^2=-1$ .

- Với mọi $z,z^{\prime }\in \mathbb{C}$, ta có:

$z+\overline{z}=2a$ (với $z=a+bi$)

$\overline{z+z^{\prime }}$ = $\overline{z}+\overline{z^{\prime }}$

$z.\overline{z}={\left|z\right|}^2={\left|\overline{z}\right|}^2$

$\overline{z{z}^{\prime }}=\overline{z}.{\overline{z}}^{\prime }$

$|z{z}^{\prime }|=|z|.|z^{\prime }|$

$|z+z^{\prime }|\le |z|+|z^{\prime }|$.

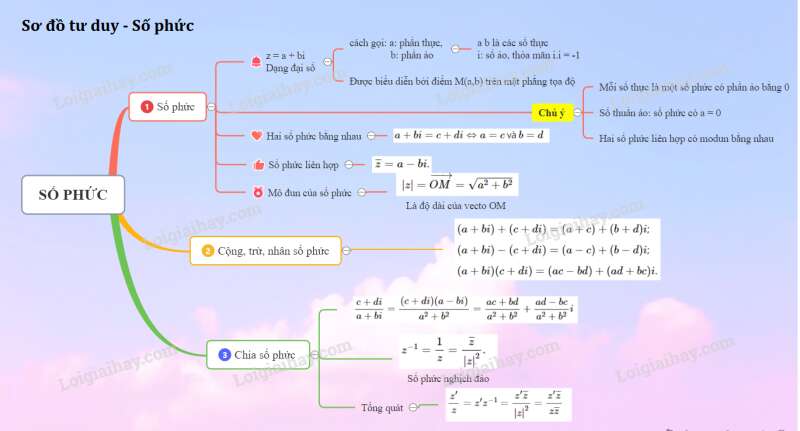
Sơ đồ tư duy về số phức