Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 12 Bài 1: Số phức chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Số phức lớp 12.
Giải bài tập Toán lớp 12 Bài 1: Số phức
Trả lời câu hỏi giữa bài
Phương pháp giải:
Số phức có phần thực là và phần ảo là .
Lời giải:
|
Số phức |
Phần thực |
Phần ảo |
Phương pháp giải:
Số phức có phần thực và phần ảo được viết là .
Lời giải:
Số phức đó là:
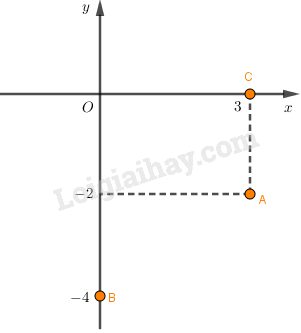
b) Các điểm biểu diễn số thực, số thuần ảo nằm ở đâu trên mặt phẳng tọa độ ?
Phương pháp giải:
Điểm biểu diễn số phức .
Lời giải:
Điểm biểu diễn số phức là .
Điểm biểu diễn số phức là .
Điểm biểu diễn số phức là .
b)
Các điểm biểu diễn số thực nằm trên , các điểm biểu diễn số ảo nằm trên
Lời giải:
Số phức là môđun bằng là
a) và ;
b) và .
Lời giải:
a)
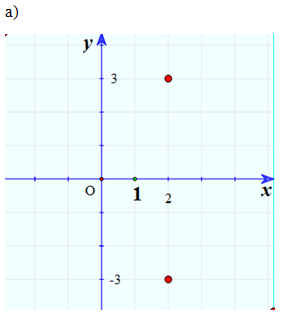
Hai điểm đối xứng nhau qua
b)
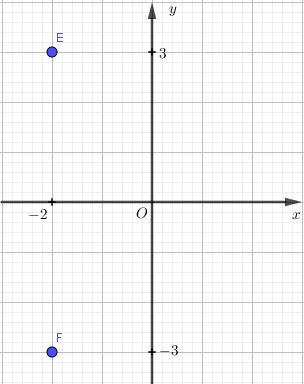
Hai điểm đối xứng nhau qua
Trả lời câu hỏi 6 trang 133 SGK Giải tích 12: Cho .
a) Hãy tính . Nêu nhận xét.
b) Tính . Nêu nhận xét.
Phương pháp giải:
a) Số phức có số phức liên hợp là .
b) Số phức có mô đun
Lời giải:
a)
Vậy
b)
Vậy
Câu hỏi và bài tập (trang 133, 134 SGK Giải tích 12)
a) ;
b) ;
c) ;
d) .
Phương pháp giải:
Cho số phức với
Ta có được gọi là phần thực của số phức và được gọi là phần ảo của số phức
Lời giải:
a)
Phần thực: , phần ảo ;
b)
Phần thực: , phần ảo ;
c)
Phần thực , phần ảo ;
d)
Phần thực , phần ảo .
a)
b)
c)
Phương pháp giải:
Cho hai số phức: và
Khi đó:
Lời giải:
a)
Từ định nghĩa bằng nhau của hai số phức, ta có:
Vậy
b)
Từ định nghĩa bằng nhau của hai số phức, ta có:
Vậy
c)
Từ định nghĩa bằng nhau của hai số phức, ta có:
.
Vậy
a) Phần thực của bằng ;
b) Phần ảo của bằng ;
c) Phần thực của thuộc khoảng ;
d) Phần ảo của thuộc đoạn ;
e) Phần thực và phần ảo của đều thuộc đoạn .
Phương pháp giải:
Cho số phức Khi đó trên mặt phẳng toạ độ , điểm là điểm biểu diễn hình học của số phức
Lời giải:
a)
Giả sử (), khi đó trên mặt phẳng toạ độ , điểm biểu diễn số phức .
Phần thực của bằng , tức là .
Vậy tập hợp các điểm biểu diễn số phức là đường thẳng trên mặt phẳng toạ độ
b)
Giả sử (), khi đó trên mặt phẳng toạ độ , điểm biểu diễn số phức .
Phần ảo của số phức bằng nên và
Vậy tập hợp điểm biểu diễn số phức là đường thẳng trên mặt phẳng .
c)
Giả sử (), khi đó trên mặt phẳng toạ độ , điểm biểu diễn số phức .
Ta có và .
Vậy tập hợp số phức cần tìm là các điểm nằm giữa hai đường thẳng và trên mặt phẳng
d)
Giả sử (), khi đó trên mặt phẳng toạ độ , điểm biểu diễn số phức .
Ta có và
Vậy tập hợp các điểm cần tìm là phần mặt phẳng nằm giữa hai đường thẳng và (kể cả các điểm trên hai đường đó).
e)
Giả sử (), khi đó trên mặt phẳng toạ độ , điểm biểu diễn số phức .
Ta có và
Vậy tập hợp các điểm cần tìm là phần mặt phẳng thuộc hình vuông (kể cả cạnh) được giới hạn bởi bốn đường thẳng .
a) ;
b) ;
c) ;
d) .
Phương pháp giải:
Cho số phức Khi đó modun của số phức được tính bởi công thức:
Lời giải:
a)
b)
c)
;
d)
a) ;
b) ;
c) ;
d) và phần ảo của bằng .
Phương pháp giải:
+) Giả sử , khi đó trên mặt phẳng toạ độ , điểm biểu diễn số phức .
+)
+) Phương trình đường thẳng có dạng:
+) Phương trình đường tròn có dạng:
Lời giải:
a)
Ta có .
Vậy tập hợp điểm biểu diễn số phức là đường tròn tâm , bán kính bằng
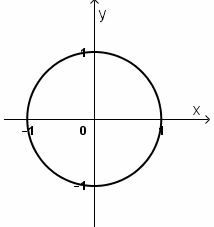
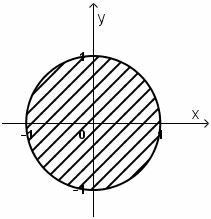
b)
Ta có .
Vậy tập hợp điểm biểu diễn số phức là hình tròn tâm , bán kính bằng (kể cả các điểm trên đường tròn).
c)
Ta có .
Vậy tập hợp điểm biểu diễn số phức z là phần nằm giữa đường tròn tâm , bán kính bằng (không kể điểm trên đường tròn này) và đường tròn tâm , bán kính bằng (kể cả các điểm trên đường tròn này).
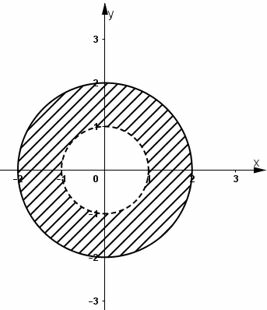
d)
Ta có và phần ảo của bằng tức . Suy ra và
Vậy tập hợp các điểm cần tìm là điểm .
a) ;
b) .
c) ;
d) .
Phương pháp giải:
Cho số phức Khi đó số phức liên hợp của là:
Lời giải:
a)
;
b)
;
c)
;
d)
.
Kiến thức cơ bản
- Số phức có phần thực là , phần ảo là ( và )
- Số phức bằng nhau và
- Số phức được biểu diễn bởi điểm trên mặt phẳng toạ độ.
- Độ dài của là môđun của số phức z, kí hiệu là
- Số phức liên hợp của và .
Chú ý
- Mỗi số thực là số phức có phần ảo bằng . Ta có .
- Số phức () là số thuần ảo (phần thực bằng )
- Số được gọi là đơn vị ảo.
- Số phức viết dưới dạng (), gọi là dạng đại số của số phức.
- Ta có:
là số thực.
là số ảo.
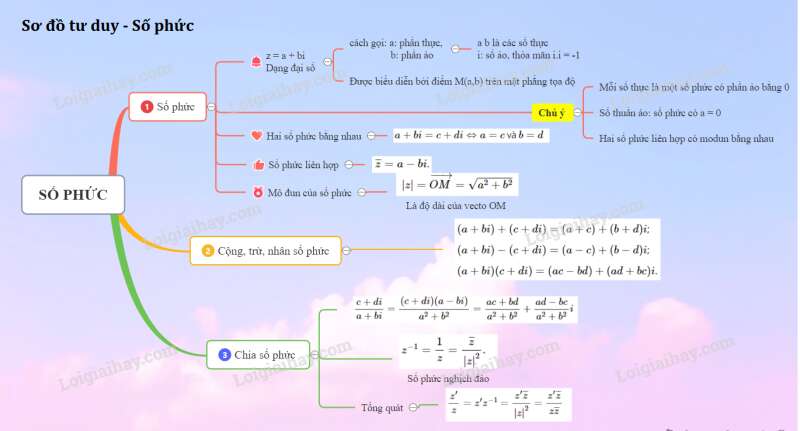
Sơ đồ tư duy về số phức