Tailieumoi.vn xin giới thiệu Bài tập Toán 12 Chương 4 Bài 1: Số phức. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 12. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 4 Bài 1: Số phức. Mời các bạn đón xem:
Bài tập Toán 12 Chương 4 Bài 1: Số phức
A. Bài tập Số phức
I. Bài tập trắc nghiệm
Bài 1: Môđun của số phức z = -3 + 4i là
A. 5
B. -3
C. 4
D. 7
Lời giải:
Ta có: z = -3 + 4i
Bài 2: Môđun của số phức z = 2 - i là
A.
B. 2 +
C. 2 -
D. 7
Lời giải:
Ta có: z = 2 - i
Bài 3: Số phức z = 1 - 2i có điểm biểu diễn là
A. M (1; 2)
B. M (1; -2)
C. M (-1; 2)
D. M (-1; -2)
Lời giải:
Số phức z = 1 - 2i có điểm biểu diễn là M(1; -2).
Bài 4: Hai điểm biểu diễn hai số phức liên hợp z = 1 + i và z− = 1 - i đối xứng nhau qua
A. Trục tung
B. Trục hoành
C. Gốc tọa độ
D. Điểm I (1; -1)
Lời giải:
Hai điểm biểu diễn của z = 1 + i và z− = 1 - i là M(1; 1) và N(1; -1) đối xứng với nhau qua trục Ox.
Bài 5: Tập hợp các điểm biểu diễn số phức z thỏa mãn |z| = 2 là
A. Hai đường thẳng
B. Đường tròn bán kính bằng 2
C. Đường tròn bán kính bằng 4
D. Hình tròn bán kính bằng 2.
Lời giải:
Gọi M là diểm biểu diễn của z. Ta có: |z| = 2 ⇔ OM = 2
Vậy quỹ tích của M là đường tròn tâm là gốc tọa độ O và bán kính R = 2.
Bài 6: Gọi A, B là các điểm biểu diễn của các số phức z1 = -1 + 2i, z2 = 2 + 3i . Khi đó, độ dài đoạn thẳng AB là
A.
B.
C.
D. 10
Lời giải:
Ta có: A(-1;2), B(2,3). Do đó:
Bài 7: Cho số phức z = 2 – 2i. Tìm khẳng định sai.
A. Phần thực của z là: 2.
B. Phần ảo của z là: -2.
C. Số phức liên hợp của z là z− = -2 + 2i.
D. Môđun của z là
Lời giải:
Số phức liên hợp của z là z− = 2 + 2i nên khẳng định C là sai.
Chọn đáp án C.
Bài 8: Cho số phức z = -1 + 3i. Phần thực, phần ảo của z− là
A. -1 và 3
B. -1 và -3
C. 1 và -3
D. -1 và -3i.
Lời giải:
Ta có z = -1 + 3i => z− = -1 - 3i
Vậy phần thực và phần ảo của z− là -1 và -3.
Chọn đáp án B.
Bài 9: Môđun của số phức z thỏa mãn z− = 8 - 6i là
A. 2
B. 10
C. 14
D. 2
Lời giải:
Ta có
Chọn đáp án B.
Bài 10: Tìm các số thực x, y sao cho (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.
A. x = 3, y = 1
B. x = 3, y = -1
C. x = -3, y = -1
D. x = -3, y = 1
Lời giải:
Ta có (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.
Vậy x = -3, y = 1.
Chọn đáp án D.
II. Bài tập tự luận có lời giải
Bài 1: Hai số phức z1 = x - 2i, z22 + yi (x, y ∈ R) là liên hợp của nhau khi
Lời giải:
Ta có z1− = x + 2i. Do đó, hai số phức đã cho gọi là liên hợp của nhau khi và chỉ khi
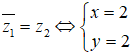
Vậy x= 2, y = 2.
Bài 2: Tập hợp các điểm biểu diễn số phức z thòa mãn |z| = |1 + i| là
Lời giải:
Ta có |1 + i| = . Gọi M là điểm biểu diễn của z ta có |z| = OM.
Do đó: |z| = |1 + i| ⇔ OM =
Vậy tập hợp các điểm M biểu diễn số phức z là đường tròn tâm O, bán kính R= .
Bài 3: Phần thực của số phức z = -i là
Lời giải:
Ta có: z = -i = 0 - i nên phần thực của số phức z = -i là 0
Bài 4: Phần ảo của số phức z = -1 là
Lời giải:
Ta có: z= -1 = -1 + 0.i nên phần ảo của số phức z = -1 là 0
Bài 5: Số phức liên hợp của số phức z = 1 + i là
Lời giải:
Số phức liên hợp của số phức z = 1 + i là z− = 1 - i
Bài 6: Cho z = 2i -1. Phần thực và phần ảo của z− là
Lời giải:
Ta có z = 2i - 1 = -1 + 2i ⇔ z− = -1 - 2i. Vậy phần thực của z− là -1 và phần ảo của z− là -2.
Bài 7: Cho số phức z = 2 – 2i. Tìm khẳng định sai.
A. Phần thực của z là: 2.
B. Phần ảo của z là: -2.
C. Số phức liên hợp của z là z− = -2 + 2i.
D. Môđun của z là
Lời giải:
Số phức liên hợp của z là z− = 2 + 2i nên khẳng định C là sai.
Bài 8 Cho số phức z = -1 + 3i. Phần thực, phần ảo của z− là?
Lời giải:
Ta có z = -1 + 3i => z− = -1 - 3i
Vậy phần thực và phần ảo của z− là -1 và -3.
Bài 9 Môđun của số phức z thỏa mãn z− = 8 - 6i là
Lời giải:
Ta có
Bài 10 Tìm các số thực x, y sao cho (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.
Lời giải:
Ta có (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.
Vậy x = -3, y = 1.
III. Bài tập vận dụng
Bài 1 Hai số phức z1 = x - 2i, z22 + yi (x, y ∈ R) là liên hợp của nhau khi?
Bài 2 Tập hợp các điểm biểu diễn số phức z thòa mãn |z| = |1 + i| là?
Bài 3 Phần thực của số phức z = -i là?
Bài 4 Phần ảo của số phức z = -1 là?
Bài 5 Gọi A, B là các điểm biểu diễn của các số phức z1 = -1 + 2i, z2 = 2 + 3i . Khi đó, độ dài đoạn thẳng AB là?
Bài 6 Số phức liên hợp của số phức z = 1 + i là?
Bài 7 Cho z = 2i -1. Phần thực và phần ảo của z− là?
Bài 8 Môđun của số phức z = -3 + 4i là?
Bài 9Gọi A, B là các điểm biểu diễn của các số phức z1 = -1 + 2i, z2 = 2 + 3i . Khi đó, độ dài đoạn thẳng AB là?
Bài 10 Hai điểm biểu diễn hai số phức liên hợp z = 1 + i và z− = 1 - i đối xứng nhau qua?
B. Lý thuyết Số phức
1. Số i.
Số i là số thỏa mãn: i2 = –1.
2. Định nghĩa số phức
Mỗi biểu thức dạng a + bi , trong đó ; i2 = –1 được gọi là một số phức.
Đối với số phức z = a + bi, ta nói: a là phần thực, b là phần ảo của z.
Tập hợp các số phức kí hiệu là C.
Ví dụ 1. Các số sau là những số phức: 2 – 3i; –8 + 4i;
Ví dụ 2. Số phức 6 – i có phần thực là 6, phần ảo là – 1.
3. Số phức bằng nhau
– Định nghĩa : Hai số phức bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau :
a + bi = c + di a = c và b = d.
Ví dụ 3. Tìm các số thực x và y biết :
(2x – 1) + (y – 2)i = 3 + (4 – y)i
Lời giải:
Ta có : (2x – 1) + (y – 2)i = 3 + (4 – y)i
Vậy x = 2 và y = 3.
– Chú ý :
a) Mỗi số thực a được coi là một số phức với phần ảo bằng 0: a = a + 0i.
Như vậy, mỗi số thực cũng là một số phức. Ta có : .
b) Số phức 0 + bi được gọi là số thuần ảo và viết đơn giản là bi : bi = 0 + bi
Đặc biệt : i = 0 + 1.i
Số i được gọi là đơn vị ảo.
Ví dụ 4. Số phức z có phần thực là và phần ảo là là .
4. Biểu diễn hình học số phức
Điểm M(a ; b) trong một hệ tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức z = a + bi.
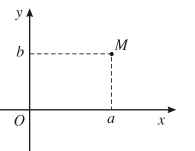
Ví dụ 5.
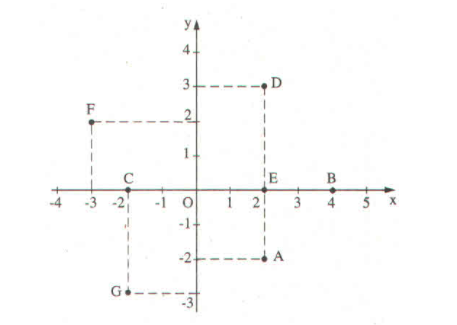
Điểm A biểu diễn số phức 2 – 2i
Điểm B biểu diễn số phức 4.
Điểm C biểu diễn số phức – 2.
Điểm D biểu diễn số phức 2 + 3i.
Điểm E biểu diễn số phức 2.
Điểm F biểu diễn số phức – 3 + 2i.
Điểm G biểu diễn số phức –2 – 3i.
5. Mô đun của số phức.
Giả sử số phức z = a + bi được biểu diễn bởi điểm M(a ; b) trên mặt phẳng tọa độ.
Độ dài của vecto được gọi là môđun của số phức z và kí hiệu là |z|.
Vậy hay .
Ta thấy:
Ví dụ 6.
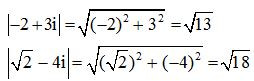
6. Số phức liên hợp
– Định nghĩa : Cho số phức z = a + bi. Ta gọi a – bi là số phức liên hợp của z và kí hiệu là .
Ví dụ 7.
Nếu z = – 3 + 5i thì .
Nếu z = – 4 + 4i thì .
– Nhận xét :
+ Trên mặt phẳng tọa độ các điểm biểu diễn z và đối xứng nhau qua trục Ox.
+ Từ định nghĩa ta có: .