Tailieumoi.vn giới thiệu Giải bài tập Toán 11 Bài 2: Phương trình lượng giác cơ bản chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Phương trình lượng giác cơ bản lớp 11.
Giải bài tập Toán 11 Bài 2: Phương trình lượng giác cơ bản
Ta có:
Do
là một giá trị của x thỏa mãn .
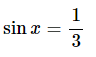
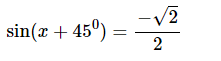
Vậy phương trình có các nghiệm là:
Vậy phương trình có nghiệm
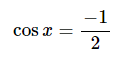
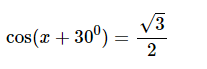
Vì = cos nên cos x = ⇔ cos x = cos
⇔ x = ± + k2π, k ∈ Z
nên
⇔
⇔
⇔ và
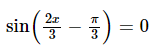
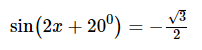
Vậy nghiệm của phương trình là hoặc
b.
Vậy nghiệm của phương trình là
Vậy nghiệm của phương trình là
d.
Vậy nghiệm của phương trình là hoặc
thỏa mãn yêu cầu bài ra khi và chỉ khi x là nghiệm của phương trình:
Vậy là nghiệm.
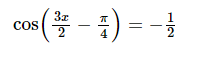
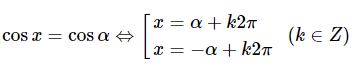
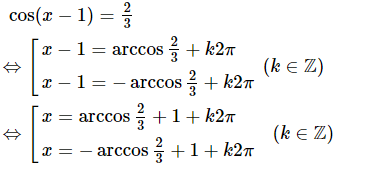

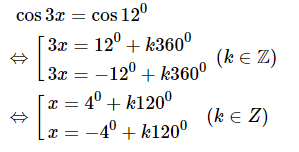
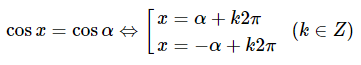
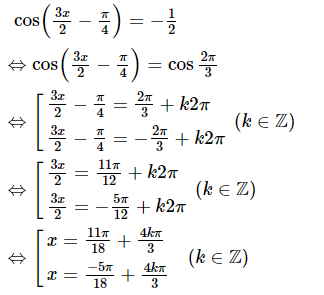
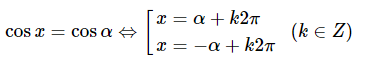
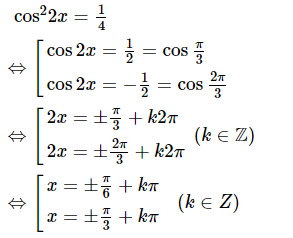
+) Tìm ĐKXĐ.
+)
+) Giải phương trình lượng giác cơ bản:
Điều kiện:
Kiểm tra ĐK:
Hay không thể nhận các giá trị chẵn.
Do đó k lẻ nên .
Vậy .
Vậy phương trình có nghiệm .
Chú ý: Nghiệm cũng có thể viết thành bằng cách đặt .
Các em cũng có thể vẽ đường tròn đơn vị để loại nghiệm như sau:
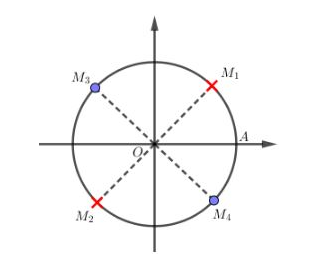
Các điểm biểu diễn là nhưng điều kiện là nên hai điểm này không lấy.
Các điểm biểu diễn là nhưng do không lấy hai điểm nên các điểm biểu diễn nghiệm chỉ còn .
Dễ thấy hai điểm này đối xứng nhau qua và nên nghiệm của phương trình là .
a.
Phương pháp giải:
Coi biểu thức sau hàm tan như một ẩn phụ khác, giải tương tự như pt LG cơ bản
Lời giải:
Điều kiện
(tm)
Vậy nghiệm của phương trình là:
b.
Phương pháp giải:
Coi biểu thức sau hàm cot như một ẩn phụ lớn, giải tương tự như pt LG cơ bản
Lời giải:
Điều kiện hay
Vậy nghiệm phương trình là
c.
Phương pháp giải:
Lưu ý điều kiện xác định của các hàm tan và cot, hàm phân thức.
Lời giải:
Điều kiện
Vậy nghiệm phương trình là: hoặc
d.
Phương pháp giải:
Lưu ý điều kiện xác định của các hàm tan và cot, hàm phân thức.
Lời giải:
ĐK:
Kết hợp với điều kiện ta thấy khi thì không thỏa điều kiện.
Vậy phương trình có nghiệm là: và .
Chú ý:
Biểu diễn các họ nghiệm trên đường tròn lượng giác để loại nghiệm:
Các nghiệm được biểu diễn bởi các điểm từ A1 đến A8 trên đường tròn lượng giác như hình dưới.
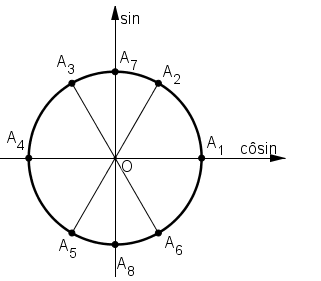
Với điều kiện x ≠ k.π nên các điểm A1 và A4 bị loại.
Vậy họ nghiệm chỉ còn lại các điểm A2; A3; A5; A6; A7; A8 và ta viết được dưới kết quả .
Bài toán tương đương giải phương trình .
B1: Coi
B2: Giải tương tự như PT
Từ đó suy ra nghiệm x và KL
Ta có:
Khi đó phương trình tương đương với:
Kết hợp điều kiện ta có:
Vậy phương trình có nghiệm:
B1: chuyển vế, đưa PT về dạng .
B2: Do PT trở về dạng với
Từ đó suy ra nghiệm x và KL.
Vậy nghiệm phương trình là: và
Cách khác:
sin3x - cos5x = 0
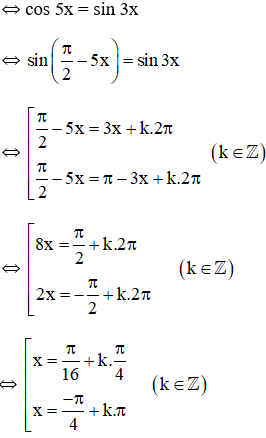
Vậy nghiệm phương trình là: và
b.
Phương pháp giải:
B1: Tìm ĐKXĐ.
B2: vì
phương trình trở về dạng với
B3: Suy ra nghiệm x rồi KL.
Lời giải:
Điều kiện:
Vậy nghiệm phương trình là .
Chú ý:
Ở bài này ta thấy ngay họ nghiệm không có nghiệm nào vi phạm điều kiện xác định nên ta lấy cả họ nghiệm và không phải loại bỏ điểm nào.
1. Phương trình lượng giác cơ bản
a) Phương trình
+) Nếu thì phương trình vô nghiệm.
+) Nếu thì phương trình có các nghiệm và
Đặc biệt:
+)
+)
b) Phương trình
+) Nếu thì phương trình vô nghiệm.
+) Nếu thì phương trình có các nghiệm và
Đặc biệt:
+)
+)
c) Phương trình
Phương trình luôn có nghiệm .
Đặc biệt:
+)
+)
d) Phương trình
Phương trình luôn có nghiệm .
Đặc biệt:
+)
+)
e) Các trường hợp đặc biệt
* Phương trình
* Phương trình
2. Một số chú ý khi giải phương trình.
- Khi giải phương trình lượng giác có chứa , chứa ẩn ở mẫu, căn bậc chẵn,…thì cần đặt điều kiện cho ẩn.
- Khi giải xong phương trình thì cần chú ý thử lại đáp án, kiểm tra điều kiện.
