Với lời giải SBT Toán 10 trang 14 Tập 2 chi tiết trong Bài 16: Hàm số bậc hai sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 16: Hàm số bậc hai

Bài 6.12 trang 14 SBT Toán 10 Tập 2: Với mỗi hàm số bậc hai cho dưới đây:

y = f(x) = –x² – x + 1; y = g(x) = x² – 8x + 8;

hãy thực hiện các yêu cầu sau:

a) Viết lại hàm số bậc hai dưới dạng y = a(x – h)² + k;

b) Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số;

c) Vẽ đồ thị của hàm số.

Lời giải:

a)

* Xét hàm số: y = f(x) = –x² – x + 1 = –(x² + x – 1)

$$\begin{gathered} =-\left(x^2+2.\frac{1}{2}.x+\frac{1}{4}-\frac{1}{4}-1\right) \\ =-\left(x^2+2.\frac{1}{2}.x+\frac{1}{4}-\frac{5}{4}\right) \\ =-{\left(x+\frac{1}{2}\right)}^2+\frac{5}{4} \end{gathered}$$

Với a = –1, h = $-\frac{1}{2}$, k = $\frac{5}{4}$.

* Xét hàm số: y = g(x) = x² – 8x + 8 = (x² – 2.4.x + 16) – 16 + 8 = (x – 4)² – 8

Với a = 1, h = 4, k = –8.

b)

- Xét hàm số: y = f(x) = –x² – x + 1 = $-{\left(x+\frac{1}{2}\right)}^2+\frac{5}{4}$

Ta có:

${\left(x+\frac{1}{2}\right)}^2\ge 0$ với mọi số thực x

$\iff -{\left(x+\frac{1}{2}\right)}^2\le 0$ với mọi số thực x

$\iff -{\left(x+\frac{1}{2}\right)}^2+\frac{5}{4}\le \frac{5}{4}$  với mọi số thực x

$\iff f\left(x\right)\le \frac{5}{4}$ với mọi số thực x

Dấu “=” xảy ra khi x = $\frac{-1}{2}$.

Vậy giá trị lớn nhất của hàm số y = f(x) là $\frac{5}{4}$ tại x = $\frac{-1}{2}$.

- Xét hàm số: y = g(x) = x² – 8x + 8 = (x – 4)² – 8

Ta có:

(x – 4)² ≥ 0 với mọi số thực x

⇔ (x – 4)² – 8 ≥ –8  với mọi số thực x

⇔ g(x) ≥ –8 

Dấu “=” xảy ra khi x = 4.

Vậy giá trị nhỏ nhất của hàm số y = g(x) là –8 tại x = 4.

c)

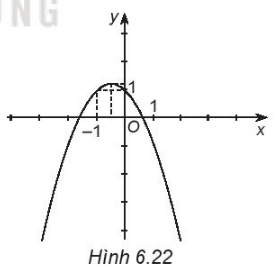
- Xét hàm số: y = f(x) = –x² – x + 1

Ta có a = –1 < 0 nên parabol quay bề lõm xuống dưới.

Đỉnh $I\left(-\frac{1}{2};\frac{5}{4}\right)$.

Trục đối xứng $x=-\frac{1}{2}$.

Giao điểm với Oy là (0; 1).

Điểm đối xứng với điểm (0; 1) qua trục đối xứng $x=-\frac{1}{2}$ là (–1; 1).

Vẽ đường cong đi qua các điểm trên ta được đồ thị hàm số y = f(x) như hình dưới.

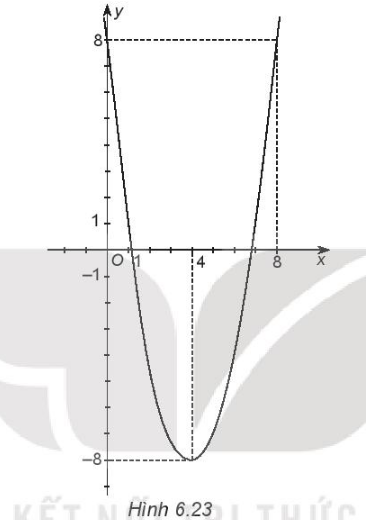
- Xét hàm số: y = g(x) = x² – 8x + 8

Ta có a = 1 > 0 nên parabol quay bề lõm lên trên.

Đỉnh I(4; – 8).

Trục đối xứng x = 4.

Giao điểm với Oy là (0; 8).

Điểm đối xứng với điểm (0; 8) qua trục đối xứng x = 4 là (8; 8).

Vẽ đường cong đi qua các điểm trên ta được đồ thị hàm số y = g(x) như hình dưới.

Bài 6.13 trang 14 SBT Toán 10 Tập 2: Tìm tập xác định và tập giá trị của các hàm số bậc hai sau:

a) f(x) = –x² + 4x – 3;

b) f(x) = x² – 7x + 12.

Lời giải:

a)

Xét hàm số f(x) = –x² + 4x – 3 có tập xác định D = ℝ

Ta có:

f(x) = –x² + 4x – 3 = –(x² – 4x + 3) = –(x² – 2.2.x + 4 – 4 + 3) = –(x – 2)² + 1

Mà:

(x – 2)² ≥ 0

⇔ –(x – 2)² ≤ 0

⇔ –(x – 2)² + 1 ≤ 1

⇔ f(x) ≤ 1

Vậy tập giá trị của f(x) = –x² + 4x – 3 là: T = (–∞; 1].

b)

Xét hàm số f(x) = x² – 7x + 12 có tập xác định D = ℝ

Ta có:

f(x) = x² – 7x + 12

$$\begin{gathered} =x^2-2.\frac{7}{2}.x+\frac{49}{4}-\frac{49}{4}+12 \\ ={\left(x-\frac{7}{2}\right)}^2-\frac{1}{4} \end{gathered}$$

Mà:

${\left(x-\frac{7}{2}\right)}^2\ge 0$

$\iff {\left(x-\frac{7}{2}\right)}^2-\frac{1}{4}\ge -\frac{1}{4}$

$\iff \mathrm{f}\left(\mathrm{x}\right)\ge -\frac{1}{4}$

Vậy tập giá trị của hàm số f(x) = x² – 7x + 12 là: T = $\left[-\frac{1}{4};+\infty \right)$.

Bài 6.14 trang 14 SBT Toán 10 Tập 2: Tìm parabol y = ax² + bx + 2, biết rằng parabol đó

a) đi qua hai điểm M(1; 5) và N(–2; 8);

b) đi qua điểm A(3; –4) và có trục đối xứng $x=-\frac{3}{2}$;

c) có đỉnh I(2; –2).

Lời giải:

a)

Do parabol y = ax² + bx + 2 đi qua M(1; 5) nên ta có:

a.1² + b.1 + 2 = 5 ⇔ a + b = 3 (1)

Do parabol y = ax² + bx + 2 đi qua N(–2; 8) nên ta có:

a.(–2)² + b.(–2) + 2 = 8 ⇔ 4a – 2b = 6 (2)

Từ (1) và (2) ta có:

$$\begin{gathered} \left\{\begin{array}{l}a+b=3\\ 4a-2b=6\end{array}\right. \\ \iff \left\{\begin{array}{l}a+b=3\\ 2a-b=3\end{array}\right.\iff \left\{\begin{array}{l}a=2\\ b=1\end{array}\right. \end{gathered}$$

Vậy parabol cần tìm là: y = 2x² + x + 2.

b)

Do parabol y = ax² + bx + 2 đi qua A(3; –4) nên ta có:

a.3² + b.3 + 2 = –4 ⇔ 9a + 3b = –6 (3)

Do parabol y = ax² + bx + 2 có trục đối xứng $x=-\frac{3}{2}$ nên ta có:

$\frac{-b}{2a}=-\frac{3}{2}$ ⇔ –2b = –6a ⇔ 6a – 2b = 0 (4)

Từ (3) và (4) ta có: 

$$\begin{gathered} \left\{\begin{array}{l}9a+3b=-6\\ 6a-2b=0\end{array}\right.\iff \left\{\begin{array}{l}3a+b=-2\\ 3a-b=0\end{array}\right. \\ \iff \left\{\begin{array}{l}a=-\frac{1}{3}\\ b=-1\end{array}\right. \end{gathered}$$

Vậy parabol cần tìm là: y = $-\frac{1}{3}{x}^2-x+2$.

c)

Do parabol y = ax² + bx + 2 có đỉnh I(2; –2) nên ta có:

$\frac{-b}{2a}=2$ ⇔ –b = 4a ⇔ 4a + b = 0 (5)

Và a.2² + b.2 + 2 = –2  ⇔ 4a + 2b = –4  (6)

Từ (5) và (6) ta có: $\left\{\begin{array}{l}4a+b=0\\ 4a+2b=-4\end{array}\right.\iff \left\{\begin{array}{l}a=1\\ b=-4\end{array}\right.$

Vậy parabol cần tìm là: y = x² – 4x + 2.

Bài 6.15 trang 14 SBT Toán 10 Tập 2: Tìm phương trình của parabol có đỉnh I(–1; 2) và đi qua điểm A(1; 6).

Lời giải:

Gọi phương trình của parabol là: y = ax² + bx + c (a ≠ 0).

+ Parabol có đỉnh I(–1; 2) nên ta có:

$\frac{-b}{2a}=-1$ ⇔ –b = –2a ⇔ 2a – b = 0 (1)

Và a.(–1)² + b.(–1) + c = 2  ⇔ a – b + c = 2 (2)

+ Parabol đi qua điểm A(1; 6) nên ta có:

a.1² + b.1 + c = 6  ⇔ a + b + c = 6 (3)

Lấy (3) trừ vế theo vế với (2) ta được: 2b = 4 ⇔ b = 2.

Thay b = 2 vào (1) ta có: 2a – 2 = 0 ⇔ a = 1 (t/m).

Thay a = 1 và b = 2 vào (2) ta có: 1 – 2 + c = 2 ⇔ c = 3.

Vậy phương trình của parabol cần tìm là: y = x² + 2x + 3.

Bài 6.16 trang 14 SBT Toán 10 Tập 2: Xác định dấu của các hệ số a, b, c và dấu của biệt thức ∆ = b² – 4ac của hàm số bậc hai y = ax² + bx + c, biết đồ thị của nó có dạng như Hình 6.16.

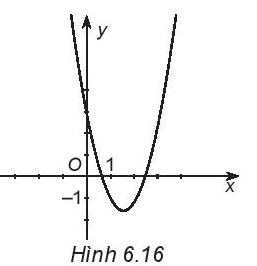
Lời giải:

Từ đồ thị của hàm số ta thấy:

+ Đồ thị quay bề lõm quay lên trên nên a > 0.

+ Đồ thị cắt trục tung tại điểm có tung độ dương nên ta có: a.0² + b.0 + c > 0 ⇔ c > 0.

+ Hoành độ đỉnh $x=-\frac{b}{2a}$ có giá trị dương nên a và b trái dấu. Vì a > 0 nên b < 0.

+ Mặt khác, vì đồ thị hàm số cắt trục hoành Ox tại hai điểm phân biệt, tức là phương trình ax² + bx + c = 0 có hai nghiệm phân biệt nên ∆ = b² – 4ac > 0.

Vậy a > 0, b < 0, c > 0 và ∆ = b² – 4ac > 0.

Bài 6.17 trang 14 SBT Toán 10 Tập 2: Bác Hùng dùng 200 m hàng rào dây thép gai để rào miếng đất đủ rộng thành một mảnh vườn hình chữ nhật.

a) Tìm công thức tính diện tích S(x) của mảnh vườn hình chữ nhật rào được theo chiều rộng x (m) của mảnh vườn đó.

b) Tìm kích thước của mảnh vườn hình chữ nhật có diện tích lớn nhất có thể rào được.

Lời giải:

a)

Chiều dài dây thép 200 m chính là chu vi của mảnh vườn hình chữ nhật. Nửa chu vi của mảnh vườn là: 100 m

Gọi chiều rộng của mảnh vườn là x (m) thì chiều dài là: 100 – x (m)

Diện tích của mảnh vườn là: S(x) = (100 – x).x = –x² + 100x  (m²).

b)

Do công thức tính diện tích S(x) là một hàm số bậc hai có a = –1 < 0 nên đồ thị của hàm S(x) là một parabol có bề lõm hướng xuống dưới, do đó, giá trị lớn nhất của S(x) là tung độ đỉnh của parabol có phương trình: y = S(x) = –x² + 100x.

Hoành độ đỉnh của parabol là: $-\frac{b}{2a}=-\frac{100}{2.(-1)}=50$.

Tung độ đỉnh của parabol là: –50² + 100.50 = 2 500.

Vậy diện tích lớn nhất có thể của mảnh vườn là 2500 m²  khi chiều rộng là 50 m và chiều dài là: 100 – 50 = 50 (m), tức là khi mảnh vườn có dạng hình vuông có độ dài cạnh là 50 m.

Xem thêm các bài giải sách bài tập Toán 10 Kết nối tri thức hay, chi tiết khác:

Giải SBT Toán 10 trang 13 Tập 2

Giải SBT Toán 10 trang 15 Tập 2

Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:

Bài 15: Hàm số

Bài 16: Hàm số bậc hai

Bài 17: Dấu của tam thức bậc hai

Bài 18: Phương trình quy về phương trình bậc hai

Bài tập cuối chương 6