Với giải sách bài tập Toán 7 Bài 2: Phân tích và xử lí số liệu sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 2: Phân tích và xử lí số liệu

Giải Toán 7 trang 9 Tập 2

Bài 5 trang 9 Toán 7 Tập 2:

Theo báo cáo của Tổng cục Hải quan, số lượng và giá trị nhập khẩu phân bón các loại của nước ta trong các năm 2017, 2018, 2019, 2020 được thống kê ở bảng sau:

 a) Tính tổng số lượng nhập khẩu phân bón các loại của nước ta trong giai đoạn từ năm 2017 đến năm 2020.

b) Số lượng nhập khẩu phân bón các loại năm 2019 giảm bao nhiêu phần trăm so với năm 2018 (làm tròn kết quả đến hàng phần mười)?

c) Giá trị nhập khẩu phân bón các loại năm 2017 gấp bao nhiêu lần giá trị nhập khẩu phân bón các loại năm 2020 (làm tròn kết quả đến hàng phần mười)?

Lời giải:

a) Dựa vào bảng số liệu ta có tổng số lượng nhập khẩu phân bón các loại của nước ta trong giai đoạn từ năm 2017 đến năm 2020 như sau:

‒ Năm 2017: 4 727,3 nghìn tấn;

‒ Năm 2018: 4 227,5 nghìn tấn;

‒ Năm 2019: 3 799,2 nghìn tấn;

‒ Năm 2020: 3 803,4 nghìn tấn.

Do đó, tổng số lượng nhập khẩu phân bón các loại của nước ta trong giai đoạn từ năm 2017 đến năm 2020 là:

4 727,3 + 4 227,5 + 3 799,2 + 3 803,4 = 16 557,4 (nghìn tấn).

b) Dựa vào bảng số liệu ta có tổng số lượng nhập khẩu phân bón các loại của nước ta năm 2018 và 2019 như sau:

‒ Năm 2018: 4 227,5 nghìn tấn;

‒ Năm 2019: 3 799,2 nghìn tấn.

Do đó, tỉ số phần trăm số lượng nhập khẩu phân bón các loại năm 2019 và năm 2018 là:

$\frac{3\mathrm{799,2}}{4\mathrm{227,5}}$  . 100% ≈ 89,9%.

Ta có: 100% - 89,9% = 10,1%.

Vậy số lượng nhập khẩu phân bón các loại năm 2019 giảm 10,1% so với năm 2018.

c) Dựa vào bảng số liệu ta có giá trị nhập khẩu phân bón các loại của nước ta năm 2017 và 2020 như sau:

‒ Năm 2017: 1 253,1 triệu đô la Mỹ;

‒ Năm 2020: 951,5 triệu đô la Mỹ.

Do đó, giá trị nhập khẩu phân bón các loại năm 2017 gấp số lần giá trị nhập khẩu phân bón các loại năm 2020 là:

$\frac{1\mathrm{253,1}}{\mathrm{951,5}}$ ≈ 1,3 (lần).

Vậy giá trị nhập khẩu phân bón các loại năm 2017 gấp 1,3 lần giá trị nhập khẩu phân bón các loại năm 2020.

Giải Toán 7 trang 10 Tập 2

Bài 6 trang 10 Toán 7 Tập 2:

Biểu đồ ở Hình 7 biểu diễn số xe máy bán ra của 5 thành viên VAMM (Hiệp hội Các nhà sản xuất xe máy Việt Nam) tại thị trường Việt Nam trong các năm 2016, 2017, 2018, 2019, 2020.

a) Lập bảng số liệu thống kê số xe máy bán ra của 5 thành viên VAMM tại thị trường Việt Nam theo mẫu sau:

 b) Tính tổng số xe máy bán ra của 5 thành viên VAMM tại thị trường Việt Nam trong giai đoạn từ năm 2016 đến năm 2020.

c) Số xe máy bán ra năm 2020 giảm bao nhiêu phần trăm so với năm 2019 (làm tròn kết quả đến hàng phần trăm)? Tìm hiểu nguyên nhân và nêu một vài lí do giải thích vì sao dẫn đến sự sụt giảm trên.

Lời giải:

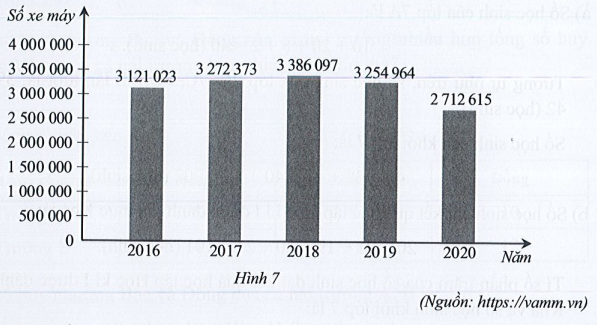
a) Nhìn vào cột biểu thị số xe máy bán ra của 5 thành viên VAMM tại thị trường Việt Nam trong năm 2016 ở Hình 7, ta thấy trên đỉnh cột ghi số 3 121 023 và đơn vị tính ghi trên trục thẳng đứng là số xe máy. Vậy số xe máy bán ra của 5 thành viên VAMM tại thị trường Việt Nam trong năm 2016 là 3 121 023 xe máy.

Tương tự như trên, ta xác định được số xe máy bán ra của 5 thành viên VAMM tại thị trường Việt Nam trong các năm 2017, 2018, 2019, 2020 lần lượt là 3 272 373, 3 386 097, 3 254 964, 2 712 615 (xe máy).

Như vậy ta có bảng số liệu thống kê số xe máy bán ra của 5 thành viên VAMM tại thị trường Việt Nam như sau:

b) Dựa vào bảng số liệu thu được ở câu a) ta có tổng số xe máy bán ra của 5 thành viên VAMM tại thị trường Việt Nam trong giai đoạn từ năm 2016 đến năm 2020 là:

3 121 023 + 3 272 373 + 3 386 097 + 3 254 964 + 2 712 615 = 15 747 072 (xe máy).

Vậy tổng số xe máy bán ra của 5 thành viên VAMM tại thị trường Việt Nam trong giai đoạn từ năm 2016 đến năm 2020 là: 15 747 072 xe máy.

c) • Dựa vào bảng số liệu ta có số xe máy bán ra của năm 2019 và năm 2020 như sau:

‒ Năm 2019: 3 254 964 xe máy;

‒ Năm 2020: 2 712 615 xe máy.

Do đó, tỉ số phần trăm số xe máy bán ra của năm 2020 so với năm 2019 là:

$\frac{2712615}{3254964}$. 100% ≈ 83,34%.

Ta có: 100% - 83,34% = 16,66%.

Vậy số xe máy bán ra năm 2020 giảm 16,66% so với năm 2019.

• Một số lí do giải thích vì sao dẫn đến sự sụt giảm trên:

+ Năm 2020 bị ảnh hưởng bởi dịch Covid ‒ 19, dẫn đến kinh tế hạn hẹp, người tiêu dùng thắt chặt chi tiêu; đồng thời Việt Nam thực hiện giãn cách xã hội, hạn chế việc di chuyển dẫn đến nhu cầu mua sắm phương tiện đi lại giảm mạnh;

+ Sức mua của thị trường đang dần bão hòa;

+ Xu hướng người tiêu dùng đang dần ưa chuộng các dòng xe máy điện hơn;

+ Khác với xe ô tô, xe máy không nhận được nhiều hỗ trợ từ nhà nước sau đại dịch Covid – 19 để khôi phục lại doanh số vốn có trước đây; …

Bài 7 trang 10 Toán 7 Tập 2:

Biểu đồ ở Hình 8 biểu diễn lực lượng lao động từ 15 tuổi trở lên của Việt Nam giai đoạn từ năm 2016 đến năm 2020.

a) Lực lượng lao động từ 15 tuổi trở lên năm 2018 nhiều hơn lực lượng lao động từ 15 tuổi trở lên năm 2017 bao nhiêu triệu người?

b) Lực lượng lao động từ 15 tuổi trở lên năm 2020 giảm bao nhiêu phần trăm so với năm 2019 (làm tròn kết quả đến hàng phần mười)?

c) Lực lượng lao động trong độ tuổi lao động năm 2020 là bao nhiêu triệu người, biết lực lượng lao động trong độ tuổi lao động năm 2020 bằng khoảng 88,5% lực lượng lao động từ 15 tuổi trở lên năm 2020 (làm tròn kết quả đến hàng phần mười)?

Lời giải:

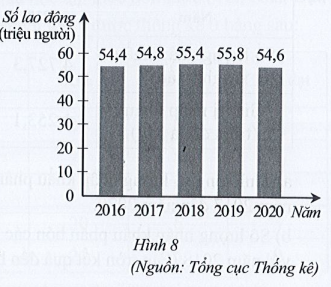
Nhìn vào cột biểu thị lực lượng lao động từ 15 tuổi trở lên của Việt Nam năm 2016 ở Hình 8, ta thấy trên đỉnh cột ghi số 54,4 và đơn vị tính ghi trên trục thẳng đứng là triệu người. Vậy lực lượng lao động từ 15 tuổi trở lên của Việt Nam năm 2016 là 54,4 triệu người.

Tương tự như trên, ta xác định được lực lượng lao động từ 15 tuổi trở lên của Việt Nam trong các năm 2017, 2018, 2019, 2020 lần lượt là 54,8; 55,4; 55,8; 54,6 (triệu người).

a) Ta có lực lượng lao động từ 15 tuổi trở lên của Việt Nam trong:

‒ Năm 2017: 54,8 triệu người;

‒ Năm 2018: 55,4 triệu người.

Do đó, lực lượng lao động từ 15 tuổi trở lên năm 2018 nhiều hơn lực lượng lao động từ 15 tuổi trở lên năm 2017 là:

55,4 – 54,8 = 0,6 (triệu người).

b) Ta có lực lượng lao động từ 15 tuổi trở lên của Việt Nam trong:

‒ Năm 2019: 55,8 triệu người;

‒ Năm 2020: 54,6 triệu người.

Do đó, tỉ số phần trăm số xe máy bán ra của năm 2020 so với năm 2019 là:

$\frac{\mathrm{54,6}}{\mathrm{55,8}}$. 100% ≈ 97,8%.

Ta có: 100% - 97,8% = 2,2%.

Vậy lực lượng lao động từ 15 tuổi trở lên năm 2020 giảm 2,2% so với năm 2019.

c) Do lực lượng lao động trong độ tuổi lao động năm 2020 bằng khoảng 88,5% lực lượng lao động từ 15 tuổi trở lên năm 2020 nên lực lượng lao động trong độ tuổi lao động năm 2020 là khoảng:

54,6 .88,5% = 54,6 . $\frac{\mathrm{88,5}}{100}$ ≈ 48,3 (triệu người).

Vậy lực lượng lao động trong độ tuổi lao động năm 2020 là khoảng 48,3 triệu người.

Giải Toán 7 trang 11 Tập 2

Bài 8 trang 11 Toán 7 Tập 2:

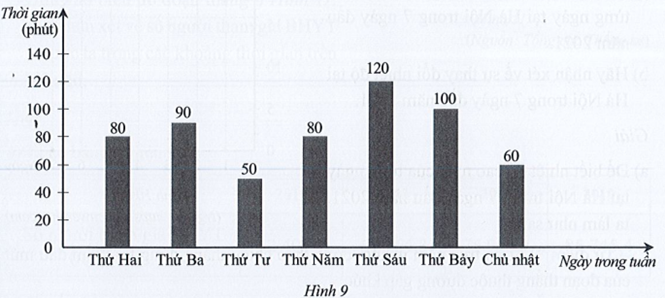
Biểu đồ ở Hình 9 biểu diễn thời gian tự luyện tập piano ở nhà các ngày trong tuần của bạn Nam.

a) Tính tổng thời gian luyện tập piano ở nhà trong cả tuần của bạn Nam.

b) Tính tỉ số phần trăm giữa tổng thời gian luyện tập piano ở nhà trong cả tuần của bạn Nam và tổng thời gian trong một tuần (làm tròn kết quả đến hàng đơn vị).

Lời giải:

a) Nhìn vào cột biểu thị thời gian tự luyện tập piano ở nhà trong ngày Thứ Hai của bạn Nam ở Hình 9, ta thấy trên đỉnh cột ghi số 80 và đơn vị tính ghi trên trục thẳng đứng là phút. Vậy thời gian tự luyện tập piano ở nhà trong ngày Thứ Hai của bạn Nam là 80 phút.

Tương tự như trên, ta xác định được thời gian tự luyện tập piano ở nhà trong các ngày Thứ Ba, Thứ Tư, Thứ Năm, Thứ Sáu, Thứ Bảy, Chủ nhật của bạn Nam lần lượt là 90, 50, 80, 120, 100, 60 (phút).

Từ đó ta có tổng thời gian tự luyện tập piano ở nhà các ngày trong tuần của bạn Nam là:

80 + 90 + 50 + 80 + 120 + 100 + 60 = 580 (phút).

Vậy tổng thời gian tự luyện tập piano ở nhà các ngày trong tuần của bạn Nam là 580 phút.

b) Đổi 1 ngày = 24 giờ, 1 tuần = 7 ngày.

Do đó, tổng thời gian của một tuần là: 7 . 24 = 168 (giờ) = 10 080 phút.

Tỉ số phần trăm giữa tổng thời gian luyện tập piano ở nhà trong cả tuần của bạn Nam và tổng thời gian trong một tuần là:

$\frac{580}{10080}$. 100% ≈ 6%.

Vậy tỉ số phần trăm giữa tổng thời gian luyện tập piano ở nhà trong cả tuần của bạn Nam và tổng thời gian trong một tuần xấp xỉ bằng 6%.

Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 1 : Thu thập, phân loại và biểu diễn dữ liệu

Bài 2 : Phân tích và xử lí số liệu

Bài 3 : Biểu đồ đoạn thẳng

Bài 4 : Biểu đồ quạt tròn

Bài 5 : Biến cố trong một số trò chơi đơn giản

Lý thuyết Phân tích và xử lí dữ liệu

1. Phân tích và xử lí dữ liệu để rút ra kết luận

Sau khi thu thập, tổ chức, phân loại, biểu diễn dữ liệu bằng bảng hoặc biểu đồ, ta cần phân tích và xử lí các dữ liệu đó để tìm ra những thông tin hữu ích và rút ra kết luận. Thông thường, quá trình phân tích và xử lí dữ liệu dựa trên tính toán và suy luận toán học.

Ví dụ: Một công ty gồm có bốn đội công nhân may áo khoác jeans. Năng suất may được số lượng áo khoác jeans của bốn đội công nhân đó trong 2 tháng đầu năm được biểu diễn như trong biểu đồ sau:

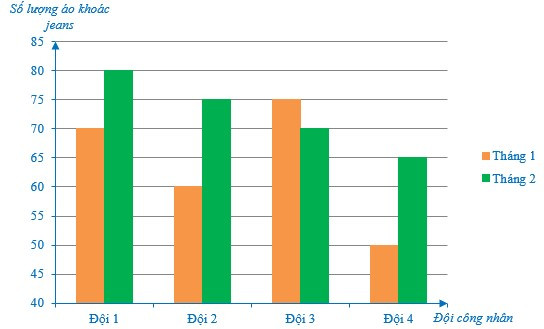
a) Sắp xếp các đội công nhân theo số lượng áo khoác jeans may được ở tháng 1 theo thứ tự từ nhỏ đến lớn.

b) Sắp xếp các đội công nhân theo số lượng áo khoác jeans may được ở tháng 2 theo thứ tự từ nhỏ đến lớn.

c) Đội công nhân nào may được nhiều nhất ở mỗi tháng?

d) Đội công nhân nào may được ít nhất ở mỗi tháng?

e) Trong cả hai tháng, đội công nhân nào có tổng số áo sơ mi may được nhiều nhất?

f) Trong cả hai tháng, đội công nhân nào có tổng số áo sơ mi may được ít nhất?

Hướng dẫn giải

a) Ta có 50 < 60 < 70 < 75 (áo khoác jeans).

Vậy khi sắp xếp các đội công nhân theo số lượng áo khoác jeans may được ở tháng 1 theo thứ tự từ nhỏ đến lớn, ta được: Đội 4; Đội 2; Đội 1; Đội 3.

b) Ta có 65 < 70 < 75 < 80 (áo khoác jeans).

Vậy khi sắp xếp các đội công nhân theo số lượng áo khoác jeans may được ở tháng 2 theo thứ tự từ nhỏ đến lớn, ta được: Đội 4; Đội 3; Đội 2; Đội 1.

c) Ở tháng 1, ta có 50 < 60 < 70 < 75 (áo khoác jeans).

Do đó ở tháng 1, Đội 3 may được nhiều áo khoác jeans nhất.

Ở tháng 2, ta có 65 < 70 < 75 < 80 (áo khoác jeans).

Do đó ở tháng 2, Đội 1 may được nhiều áo khoác jeans nhất.

Vậy đội công nhân may được nhiều áo khoác jeans nhất ở tháng 1, tháng 2 lần lượt là Đội 3 và Đội 1.

d) Ở tháng 1, ta có 50 < 60 < 70 < 75 (áo khoác jeans).

Do đó ở tháng 1, Đội 4 may được ít áo khoác jeans nhất.

Ở tháng 2, ta có 65 < 70 < 75 < 80 (áo khoác jeans).

Do đó ở tháng 2, Đội 4 may được ít áo khoác jeans nhất.

Vậy đội công nhân may được ít áo khoác jeans nhất ở tháng 1, tháng 2 đều là Đội 4.

e) Tổng số áo khoác jeans Đội 1 may được ở cả hai tháng là:

70 + 80 = 150 (áo khoác jeans).

Tổng số áo khoác jeans Đội 2 may được ở cả hai tháng là:

60 + 75 = 135 (áo khoác jeans).

Tổng số áo khoác jeans Đội 3 may được ở cả hai tháng là:

75 + 70 = 145 (áo khoác jeans).

Tổng số áo khoác jeans Đội 4 may được ở cả hai tháng là:

50 + 65 = 115 (áo khoác jeans).

Ta có 115 < 135 < 145 < 150 (áo khoác jeans).

Vậy trong cả hai tháng, Đội 1 có tổng số áo sơ mi may được nhiều nhất.

f) Ta có 115 < 135 < 145 < 150 (áo khoác jeans).

Vậy trong cả hai tháng, Đội 4 có tổng số áo sơ mi may được ít nhất.

2. Tính hợp lí của kết luận thống kê

Quá trình phân tích và xử lí dữ liệu giúp chúng ta có thể nhận biết được: tính hợp lí của dữ liệu thống kê, tính hợp lí của kết luận thống kê và ta cũng có thể bác bỏ kết luận đã nêu ra. Thông thường, để làm được điều đó ta dựa trên những tiêu chí đơn giản hoặc dựa trên tính toán và suy luận toán học.

Ví dụ: Một huấn luyện viên dạy bơi sải ghi lại thời gian (tính theo buổi, mỗi buổi 90 phút) thành thạo môn bơi sải của các học viên như bảng bên:

a) Huấn luyện viên đã khảo sát tổng cộng bao nhiêu học viên?

b) Biết rằng học viên có năng khiếu về môn bơi lội sẽ thành thạo bơi sải trong vòng 8 buổi học. Huấn luyện viên đã đưa ra kết luận rằng: Sau khi khảo sát, số học viên có năng khiếu về môn bơi lội chiếm tỉ lệ 15% so với tổng số học viên tham gia khảo sát. Hỏi kết luận đó của huấn luyện viên có đúng không?

Hướng dẫn giải

a) Số học viên mà huấn luyện viên đã khảo sát là:

1 + 2 + 3 + 10 + 13 + 7 + 4 = 40 (học viên).

Vậy huấn luyện viên đã khảo sát tổng cộng là 40 học viên.

b) Số học viên được huấn luyện viên đánh giá là có năng khiếu về môn bơi lội là:

1 + 2 + 3 = 6 (học viên).

So với tổng số học viên tham gia khảo sát, tỉ lệ học viên được đánh giá là có năng khiếu về môn bơi lội là:

$\frac{6.100}{40}\%=15\%$.

Vậy huấn luyện viên đã kết luận đúng.