Với giải bài 53 trang 87 Toán lớp 8 chi tiết trong Bài 9: Ứng dụng thực tế của tam giác đồng dạng giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Giải bài tập Toán lớp 8 Bài 9: Ứng dụng thực tế của tam giác đồng dạng

Bài 53 trang 87 Toán 8 Tập 2: Một người đo chiều cao của một cây nhờ một cọc chôn xuống đất, cọc cao 2m và đặt xa cây 15m. Sau khi người ấy lùi ra xa cách cọc 0,8m thì nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng. Hỏi cây cao bao nhiêu, biết rằng khoảng cách từ chân đến mắt người ấy là 1,6m?

Lời giải:

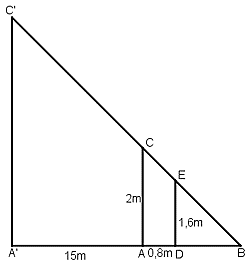
Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.

Khoảng cách từ chân đến mắt người đo là DE = 1,6m.

Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.

Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B

⇒ A’C’ // AC // DE.

Ta có: ΔDEB $~$ ΔACB (vì DE // AC).

$\Rightarrow \frac{DE}{AC}=\frac{DB}{AB}$

Thay số:

 $$\begin{gathered} \frac{1,6}{2}=\frac{DB}{AB} \\ \Rightarrow \frac{DB}{AB}=\frac{4}{5} \\ \Rightarrow \frac{DB}{4}=\frac{AB}{5} \end{gathered}$$

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$$\begin{gathered} \frac{DB}{4}=\frac{AB}{5} \\ =\frac{AB-DB}{5-4} \\ =\frac{AD}{1}=0,8 \end{gathered}$$

Suy ra:

$\begin{array}{l}\frac{DB}{4}=0,8\Rightarrow DB=3,2\\ \frac{AB}{5}=0,8\Rightarrow AB=4\end{array}$

⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m

+ Ta có: ΔACB $~$ ΔA’C’B (vì AC // A’C’)

Nên

 $$\begin{gathered} \frac{AB}{A\text{'}B}=\frac{AC}{A\text{'}C\text{'}} \\ \Rightarrow A\text{'}C\text{'}=\frac{AC.A\text{'}B}{AB} \\ =\frac{2.19}{4}=9,5m \end{gathered}$$

Vậy cây cao 9,5m.

Xem thêm lời giải bài tập Toán lớp 8 hay, chi tiết khác:

Bài 54 trang 87 Toán 8 Tập 2: Để đo khoảng cách giữa hai điểm A và B, trong đó B không tới được, người ta tiến hành đo và tính khoảng cách AB như hình 57; AB // DF; AD = m; DC = n; DF = a...

Bài 55 trang 87 Toán 8 Tập 2: Hình 58 dưới đây mô tả dụng cụ đo bề dày của một số loại sản phẩm. Dụng cụ này gồm thước AC được chia đến 1mm và gắn với một bản kim loại hình tam giác ABD, khoảng cách BC = 10mm...