Bài tập về Ứng dụng thực tế của tam giác đồng dạng chọn lọc

Quý Lê Xuân Ngày: 08-03-2024 Lớp 8

Tải xuống 4 9.7 K 58

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập Ứng dụng thực tế của tam giác đồng dạng Toán lớp 8, tài liệu bao gồm 4 trang, tuyển chọn bài tập Ứng dụng thực tế của tam giác đồng dạng đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có đáp án (có lời giải), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Ứng dụng thực tế của tam giác đồng dạng gồm các nội dung chính sau:

A. Lý thuyết

- tóm tắt lý thuyết ngắn gọn.

B. Luyện tập

- gồm 3 bài tập vận dụng có đáp án và lời giải chi tiết giúp học sinh tự rèn luyện cách giải các dạng bài tập Ứng dụng thực tế của tam giác đồng dạng.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

Ứng dụng thực tế của tam giác đồng dạng (ảnh 1)

ỨNG DỤNG THỰC TẾ CỦA TAM GIÁC ĐỒNG DẠNG

1. ĐO GIÁN TIẾP CHIỀU CAO CỦA VẬT

Bài toán: Xác định chiều cao của một vật (tòa nhà).

Phương pháp thực hiện

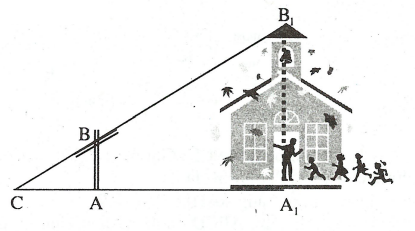
Ứng dụng thực tế của tam giác đồng dạng (ảnh 2)

Chúng ta sẽ tiến hành theo hai bước:

Bước 1: Tiến hành đo đạc

Đặt cọc AB thẳng đứng trên đó có gắn một thước ngắm quay được quanh một cái chốt của cọc.
Điều chỉnh thước ngắm sao cho hướng của thước đi qua đỉnh $B_{1}$ của tòa nhà, sau đó xác định giao điểm C của đường thẳng $A A_{1}$ với $B B_{1}$ .
Đo khoảng cách $A C, A A_{1}$ .

Bước 2: Tính chiều cao: Ta có:

$Δ A_{1} B_{1} C_{1} ∽ Δ A B C \Rightarrow \frac{A_{1} B_{1}}{A B} = \frac{A_{1} C}{A C} \Leftrightarrow A_{1} B_{1} = \frac{A_{1} C . A B}{A C}$ .

2. ĐO KHOẢNG CÁCH GIỮA HAI ĐỊA ĐIỂM TRONG ĐÓ CÓ MỘT ĐỊA ĐIỂM KHÔNG THỂ TỚI ĐƯỢC

Bài toán: Xác định khoảng cách AB, trong đó địa điểm A không thể tới được.

Phương pháp thực hiện

Chúng ta sẽ tiến hành theo hai bước:

Bước 1: Tiến hành đo đạc

Chọn một khoảng bằng phẳng rồi vạch một đoạn BC và đo độ dài của nó (giả sử $B C = a$ ).
Dùng thước đo góc, đo các góc $\hat{A B C} = α, \hat{A C B} = β$ .

Bước 2: Tính khoảng cách AB

Thực hiện vẽ trên giấy $Δ A_{1} B_{1} C_{1}$ thỏa mãn:

$B_{1} C_{1} = a_{1}, \hat{A_{1} B_{1} C_{1}} = α, \hat{A_{1} C_{1} B_{1}} = β$

Nhận xét rằng:

$Δ A_{1} B_{1} C_{1} ∽ Δ A B C \Rightarrow \frac{A_{1} B_{1}}{A B} = \frac{B_{1} C_{1}}{B C} \Leftrightarrow A B = \frac{A_{1} B_{1} . B C}{B_{1} C_{1}}$ .

B. LUYỆN TẬP

VÍ DỤ 1. Một người đo chiều cao của một cây nhờ chôn một cọc xuống đất, cọc cao 2m và đặt xa cây 15m. Sau khi người lùi xa cách cọc 0,8m thì nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng. Hỏi cây cao bao nhiêu mét, biết rằng khoảng cách từ chân đến mắt người ấy là 1,6m?

Xem thêm