Cho hình thoi ABCD có góc A bằng 60 độ. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA

Đức Long Ngày: 12-10-2022 Lớp 8

2.8 K

Với giải bài 3 trang 115 Toán lớp 8 chi tiết trong Bài 1: Đa giác. Đa giác đều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Giải bài tập Toán lớp 8 Bài 1: Đa giác. Đa giác đều

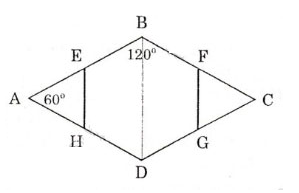
Bài 3 trang 115 Toán 8 Tập 1:Cho hình thoi ABCD có góc $\hat{A} = 60 °$ . Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng đa giác EBFGDH là lục giác đều.

Lời giải:

Ta có: $A E = E B = \frac{A B}{2}$ (E là trung điểm của AB)

$B F = F C = \frac{B C}{2}$ (F là trung điểm của BC)

$C G = G D = \frac{C D}{2}$ (G là trung điểm của CD)

$A H = H D = \frac{A D}{2}$ (H là trung điểm của AD)

Vì ABCD là hình thoi nên AB = BC = CD = AD

Suy ra BE = AE = BF = FC = CG = GD = AH = HD = $\frac{A B}{2}$ . (1)

Xét $Δ A B D$ , có: BA = DA nên $Δ A B D$ cân tại A

Mà $\hat{A} = 60 °$

Suy ra $Δ A B D$ đều

$\Rightarrow A B = B D = A D$

Ta lại có:

E là trung điểm của AB

H là trung điểm của AD

Suy ra EH là đường trung bình của

$\Rightarrow E H = \frac{B D}{2} = \frac{A B}{2}$ (2)

Xét $Δ C B D$ , có: BC = CD nên $Δ C B D$ cân tại C

Mà $\hat{C} = \hat{A} = 60 °$ (tính chất hình thoi)

Suy ra $Δ C B D$ đều

$\Rightarrow C B = B D = C D$

Ta lại có:

F là trung điểm của CB

G là trung điểm của CD

Suy ra FG là đường trung bình của $Δ C B D$

$\Rightarrow F G = \frac{B D}{2} = \frac{A B}{2}$ (3)

Từ (1), (2) và (3) suy ra:

BE = AE = BF = FC = CG = GD = AH = HD = EH = FG

Hay EB = BF = FG = GD = DH = HE.

Vì ABCD là hình thoi nên AD // BC

$\begin{array}{l} \Rightarrow \hat{A} + \hat{A B C} = 180 ° \\ \Leftrightarrow 60 ° + \hat{A B C} = 180 ° \\ \Leftrightarrow \hat{A B C} = 180 ° - 60 ° = 120 ° \\ \Rightarrow \hat{A D C} = \hat{A B C} = 120 ° \end{array}$