Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Bài 7: Trường hợp đồng dạng thứ ba hay, chi tiết giúp học sinh dễ dàng làm bài tập Trường hợp đồng dạng thứ ba lớp 8.

Giải bài tập Toán lớp 8 Bài 7: Trường hợp đồng dạng thứ ba

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 78 Toán 8 Tập 2: Trong các tam giác dưới đây, những cặp tam giác nào đồng dạng với nhau ? Hãy giải thích (h.41)

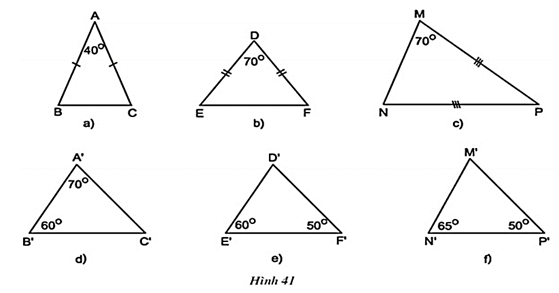
Lời giải:

Xét ΔABC có

 $$\begin{gathered} \widehat{A}\text{\hspace{0.17em}\hspace{0.17em}}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{B}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{C}={180}^0 \\ \Rightarrow \widehat{B}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{C}={180}^0-\widehat{A} \end{gathered}$$

Mà ΔABC cân tại A nên  $\widehat{B}=\widehat{C}$.

⇒ $\widehat{B}=\widehat{C}=\frac{{180}^0-{40}^0}{2}={70}^0$

Vì ΔMNP cân tại P ⇒ $\widehat{M}=\widehat{N}$ = 70^o

Xét ΔABC và ΔPMN có

$\widehat{B}=\widehat{M}$ = 70^o

$\widehat{C}=\widehat{N}$ = 70^o

⇒ ΔABC $~$ ΔPMN (g.g)

Xét ΔA’B’C’ có

$$\begin{gathered} \widehat{A\text{'}}\text{\hspace{0.17em}\hspace{0.17em}}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{B\text{'}}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{C\text{'}}={180}^0 \\ \Rightarrow \widehat{C\text{'}}={180}^0-\widehat{A\text{'}}-\widehat{B\text{'}} \\ ={180}^0-{70}^0-{60}^0={50}^0 \end{gathered}$$

Xét ΔA’B’C’ và ΔD’E’F’ có:

$\widehat{B\text{'}}=\widehat{E\text{'}}$ (= 60^o)

$\widehat{C\text{'}}=\widehat{F\text{'}}$ (= 50^o)

⇒ ΔA’B’C’ $~$ ΔD’E’F’ (g.g).

Câu hỏi 2 trang 79 Toán 8 Tập 2: Ở hình 42 cho biết AB = 3cm; AC = 4,5cm và $\widehat{ABD}=\widehat{BCA}$.

a) Trong hình vẽ này có bao nhiêu tam giác? Có cặp tam giác nào đồng dạng với nhau không ?

b) Hãy tính các độ dài x và y (AD = x, DC = y).

c) Cho biết thêm BD là tia phân giác của góc B. Hãy tính độ dài các đoạn thẳng BC và BD.

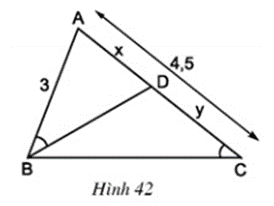
Lời giải:

a) Trong hình vẽ có 3 tam giác: ΔABD, ΔCBD, ΔABC

+ Xét ΔABD và ΔACB có

$\widehat{ABD}=\widehat{C}$

$\widehat{A}$ chung

⇒ ΔABD $~$ ΔACB (g.g)

b) Theo a ta có : ΔABD $~$ΔACB nên:

$$\begin{gathered} \frac{AB}{AC}=\frac{AD}{AB}\Rightarrow \frac{3}{4,5}=\frac{AD}{3} \\ \Rightarrow AD=x=\frac{3.3}{4,5}=2 \end{gathered}$$

Suy ra: y = 4,5 – 2 = 2,5.

c) Do BD là tia phân giác của góc B nên theo tính chất đường phân giác ta có:

$$\begin{gathered} \frac{AB}{BC}=\frac{x}{y}\Rightarrow \frac{3}{BC}=\frac{2}{2,5} \\ \Rightarrow BC\frac{3.2,5}{2}=3,75 \end{gathered}$$

+ Do ∆ABD $~$ ∆ACB nên:

$$\begin{gathered} \frac{AB}{AC}=\frac{BD}{CB} \\ \Rightarrow \frac{3}{4,5}=\frac{BD}{3,75} \\ \Rightarrow BD=2,5 \end{gathered}$$

Bài tập (trang 79; 80)

Bài 35 trang 79 Toán 8 Tập 2: Chứng minh rằng nếu tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k thì tỉ số của hai đường phân giác tương ứng của chúng cũng bằng k.

Lời giải:

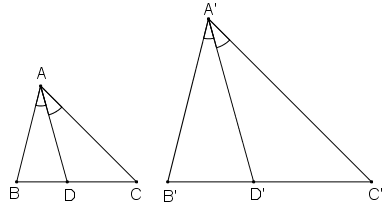
Gọi AD và A’D' lần lượt là hai đường phân giác của ΔABC và ΔA'B'C'.

Vì ∆A’B’C’$~$ ∆ABC theo tỉ số k nên;

$\widehat{B\text{'}}=\widehat{B};\widehat{A\text{'}}=\widehat{A};\frac{A\text{'}B\text{'}}{AB}=k$.

+) Lại có: AD, A’D’ lần lượt là phân giác của góc A và góc A’ nên:

$$\begin{gathered} \widehat{B\text{'}A\text{'}D\text{'}}=\frac{1}{2}\widehat{B\text{'}A\text{'}C\text{'}}; \\ \widehat{BAD}=\frac{1}{2}\widehat{BAC} \\ \Rightarrow \widehat{B\text{'}A\text{'}D\text{'}}=\widehat{BAD} \end{gathered}$$

+ Xét ∆A’B’D’ và ∆ABD  có:

$\begin{array}{l}\widehat{B\text{'}}=\widehat{B}\\ \widehat{B\text{'}A\text{'}D\text{'}}=\widehat{BAD}\end{array}$

Suy ra: ∆A’B’D’ $~$∆ABD

Suy ra: $\frac{A\text{'}D\text{'}}{AD}=\frac{A\text{'}B\text{'}}{AB}=k$.

Bài 36 trang 79 Toán 8 Tập 2: Tính độ dài x của đoạn thẳng BD trong hình 43 (làm tròn đến chữ số thập phân thứ nhất), biết rằng ABCD là hình thang (AB // CD); AB = 12,5cm, CD = 28,5cm, $\widehat{DAB}=\widehat{DBC}$.

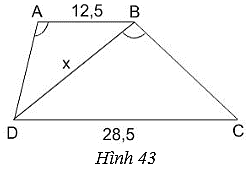
Lời giải:

Vì AB // CD nên $\widehat{ABD}=\widehat{BDC}$(so le trong)

Xét ∆ABD và ∆BDC có:

$\widehat{DAB}=\widehat{DBC}$ (giả thiết).

$\widehat{ABD}=\widehat{BDC}$(chứng minh trên)

Suy ra: ∆ABD $~$ ∆BDC  (g - g).

Suy ra:

$$\begin{gathered} \frac{AB}{BD}=\frac{DB}{DC} \\ \Rightarrow B{D}^2=AB.DC \\ \Rightarrow BD=\sqrt{AB.DC} \\ =\sqrt{12,5.28,5}\approx 18,87cm \end{gathered}$$

Vậy x ≈ 18,87 cm.

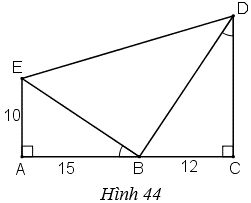
Bài 37 trang 79 Toán 8 Tập 2: Hình 44 cho biết $\widehat{EBA}=\widehat{BDC}$.

a) Trong hình vẽ có bao nhiêu tam giác vuông? Hãy kể tên các tam giác đó.

b) Cho biết AE = 10cm, AB = 15cm, BC = 12cm. Hãy tính độ dài các đoạn thẳng CD, BE, BD và ED (làm tròn đến chữ số thập phân thứ nhất).

c) So sánh diện tích tam giác BDE với tổng diện tích của hai tam giác AEB và BCD.

Lời giải:

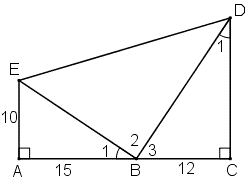
a) + ΔABE vuông tại A.

+ ΔBCD vuông tại C.

+ Ta có: $\widehat{B_3}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{D_1}={90}^0$

Mà $\widehat{D_1}=\widehat{B_1}$ ( giả thiết)

Suy ra: $\widehat{B_3}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{B_1}={90}^0$

$\Rightarrow \widehat{B_2}={180}^0-\left(\widehat{B_3}+\text{\hspace{0.17em}\hspace{0.17em}}\widehat{B_1}\right)={90}^0$.

Vậy ΔBED vuông tại B.

b)

+ Áp dụng định lý Py – ta - go trong ΔABE vuông tại A ta có:

EB² = AE² + AB² = 10² + 15² = 325

$\Rightarrow EB=5\sqrt{13}\approx 18$cm.

+ Xét ∆ABE và ∆CDB có:

$\begin{array}{l}\widehat{A}=\widehat{C}={90}^0\\ \widehat{B_1}=\widehat{D_1}\end{array}$

Suy ra: ∆ABE $~$ ∆ADB( g.g).

$$\begin{gathered} \Rightarrow \frac{AB}{CD}=\frac{BE}{BD}=\frac{EA}{BC} \\ \Rightarrow \frac{15}{CD}=\frac{5\sqrt{13}}{DB}=\frac{10}{12} \\ \Rightarrow CD=18;DB=6\sqrt{13}\approx 21,6cm \end{gathered}$$

+ Áp dụng định lý Py – ta - go trong ΔEBD vuông tại B ta có:

$$\begin{gathered} E{D}^2=E{B}^2\text{}+\text{\hspace{0.17em}}B{D}^2 \\ ={\left(5\sqrt{13}\right)}^2+\text{\hspace{0.17em}}{\left(6\sqrt{13}\right)}^2=793 \\ \Rightarrow ED\approx 28,2cm \end{gathered}$$

Vậy BE $\approx$ 18cm; CD = 18cm; BD $\approx$ 21,6cm; $ED\approx$28,2cm

c) Ta có:

$S_{BDE}=\frac{1}{2}BE.BD$

$\hspace{0.17em}=\frac{1}{2}.5\sqrt{13}.6\sqrt{13}=195$ ( $c{m}^2$ )

$S_{ABE}=\frac{1}{2}EA.AB$

$\hspace{0.17em}=\frac{1}{2}.10.15=75$ ( $c{m}^2$)

$S_{BCD}=\frac{1}{2}BC.CD$

$=\frac{1}{2}.12.18=108$ ( $c{m}^2$)

$$\begin{gathered} \Rightarrow S_{ABE}+S_{BCD}=75+108 \\ =183<S_{BDE} \end{gathered}$$

Bài 38 trang 79 Toán 8 Tập 2: Tính độ dài x, y của các đoạn thẳng trong hình 45.

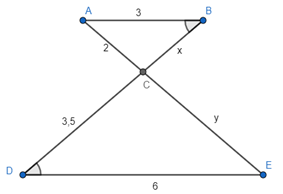
Hình 45

Lời giải:

 $\widehat{ABD}=\widehat{BDE}$ (giả thuyết)

 $\widehat{ACB}=\widehat{DCE}$(đối đỉnh)

Xét tam giác ABC và tam giác EDC có:
 $\left\{\begin{array}{l}\widehat{ABC}=\widehat{CDE}\\ \widehat{ACB}=\widehat{DCE}\end{array}\right.$(chứng minh)

Do đó, ∆ABC $~$ ∆ EDC.

$\Rightarrow \frac{AB}{ED}=\frac{BC}{DC}=\frac{AC}{EC}$ (các cặp cạnh tương ứng)

Thay số:

$$\begin{gathered} \frac{3}{6}=\frac{x}{3,5}=\frac{2}{y} \\ \Rightarrow x=\frac{3.3,5}{6}=1,75; \\ y=\frac{6.2}{3}=4 \end{gathered}$$

Bài 39 trang 79 Toán 8 Tập 2: Cho hình thang ABCD (AB // CD). Gọi O là giao điểm của hai đường chéo AC và BD.

a) Chứng minh rằng OA.OD = OB.OC

b) Đường thẳng qua O vuông góc với AB và CD theo thứ tự tại H và K.

Chứng minh rằng  $\frac{OH}{OK}=\frac{AB}{CD}$.

Lời giải:

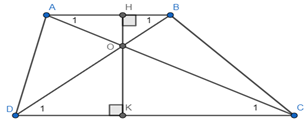
a) Xét ∆AOB và ∆ COD có:

$\widehat{A_1}=\widehat{C_1}$ (hai góc so le trong).

$\widehat{B_1}=\widehat{D_1}$ (hai góc so le trong).

Suy ra: ∆AOB $~$  ∆ COD (g.g)

$\Rightarrow \frac{AO}{OC}=\frac{OB}{OD}$

Suy ra: AO.OD = OB. OC.

b) Theo a ta có: ∆AOB  $~$ ∆ COD

Suy ra: $\frac{OA}{OC}=\frac{AB}{CD}\left(1\right)$

Xét ∆AOH và ∆COK có: 

$$\begin{gathered} \widehat{A_1}=\widehat{C_1} \\ \widehat{H}=\widehat{K}={90}^0 \end{gathered}$$

Suy ra: ∆AOH $~$ ∆COK (g.g.).

Suy ra: $\frac{OH}{OK}=\frac{AO}{OC}\left(2\right)$

Từ (1) và (2) suy ra:

$\frac{OH}{OK}=\frac{AB}{CD}$ (đpcm).

Bài 40 trang 80 Toán 8 Tập 2: Cho tam giác ABC, trong đó AB = 15cm, AC = 20cm. Trên hai cạnh AB và AC lần lượt lấy hai điểm D và E sao cho AD = 8cm, AE = 6cm. Hai tam giác ABC và ADE có đồng dạng với nhau không? Vì sao?

Lời giải:

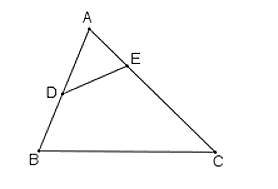
Ta có:

 $$\begin{gathered} \frac{AE}{AB}=\frac{6}{15}=\frac{2}{5}; \\ \frac{AD}{AC}=\frac{8}{20}=\frac{2}{5} \end{gathered}$$

Suy ra: $\frac{AE}{AB}=\frac{AD}{AC}$.

Xét ∆ADE và ∆ACB có:

$\widehat{A}$ chung

$\frac{AE}{AB}=\frac{AD}{AC}$

Suy ra: ∆ADE $~$ ∆ACB.

Bài 41 trang 80 Toán 8 Tập 2: Tìm các dấu hiệu để nhận biết hai tam giác cân đồng dạng.

Lời giải:

+ Nếu cạnh bên và cạnh đáy của tam giác cân này tỉ lệ với cạnh bên và cạnh đáy của tam giác cân kia thì hai tam giác đó đồng dạng.

+ Nếu hai tam giác cân có hai góc ở đỉnh bằng nhau thì hai tam giác cân đồng dạng.

+ Nếu góc ở đáy của tam giác cân này bằng góc ở đáy của tam giác cân kia thì hai tam giác cân đó đồng dạng.

Bài 42 trang 80 Toán 8 Tập 2: So sánh các trường hợp đồng dạng của tam giác với các trường hợp bằng nhau của tam giác (nêu lên những điểm giống nhau và khác nhau).

Lời giải:

So sánh:

Bài 43 trang 80 Toán 8 Tập 2: Cho hình bình hành ABCD (h.46) có độ dài các cạnh AB = 12cm, BC = 7cm. Trên cạnh AB lấy một điểm E sao cho AE = 8cm. Đường thẳng DE cắt cạnh CB kéo dài tại F.

a) Trong hình vẽ đã cho có bao nhiêu cặp tam giác đồng dạng với nhau? Hãy viết các cặp tam giác đồng dạng với nhau theo các đỉnh tương ứng.

b) Tính độ dài các đoạn thẳng EF và BF, biết rằng DE = 10cm.

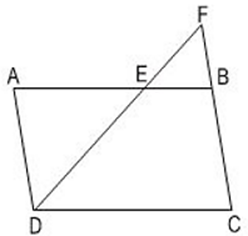
Hình 46

Lời giải:

a) Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác mới đồng dạng với tam giác đã cho.

Xét ΔFCD có EB // CD (E ∈ FD, B ∈ FC)

⇒ ΔFEB $~$ ΔFDC (1)

Xét ΔAED có FB // AD (F ∈ DE, B ∈ AE)

⇒ ΔFEB $~$ ΔDEA (2)

Từ (1) và (2) suy ra: ΔDEA $~$ ΔFDC (tính chất bắc cầu).

b) AB = 12cm, AE = 8cm

⇒ EB = AB – AE = 12 - 8 = 4cm.

Vì ABCD là hình bình hành nên AD = BC = 7cm

Do ΔFEB  $~$ ΔDEA

Suy ra:

 $$\begin{gathered} \frac{EF}{DE}=\frac{EB}{EA}=\frac{BF}{AD} \\ \Rightarrow \frac{EF}{10}=\frac{4}{8}=\frac{BF}{7} \end{gathered}$$

⇒ EF = $\frac{4}{8}.10$= 5cm, BF = $7.\frac{4}{8}$  = 3,5cm.

Bài 44 trang 80 Toán 8 Tập 2: Cho tam giác ABC có các cạnh AB = 24cm, AC = 28cm. Tia phân giác của góc A cắt cạnh BC tại D. Gọi M, N theo thứ tự là hình chiếu của B và C trên đường thẳng AD.

a) Tính tỉ số $\frac{BM}{CN}$;

b) Chứng minh $\frac{AM}{AN}=\frac{DM}{DN}$.

Lời giải:

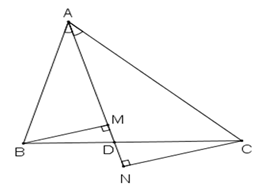
a) Xét ∆ABM và ∆ACN có:

$$\begin{gathered} \widehat{BAD}=\widehat{CAN} \\ \widehat{M}=\widehat{N}\left(={90}^0\right) \end{gathered}$$

Suy ra: ∆ABM $~$ ∆ACN ( g.g).

Suy ra: $\frac{BM}{CN}=\frac{AB}{AC}=\frac{24}{28}=\frac{6}{7}$.

b) Theo ý a ta có:  ∆ABM $~$ ∆ACN

Suy ra: $\frac{AM}{AN}=\frac{BM}{CN}\left(1\right)$

Xét ∆BMD và ∆CND có:

$\widehat{M}=\widehat{N}\left(={90}^0\right)$

$\widehat{BDM}=\widehat{CDN}$ ( đối đỉnh).

Suy ra: ∆BMD $~$ ∆CND ( g.g)

 $\Rightarrow \frac{BM}{CN}=\frac{DM}{DN}$  (2).

Từ (1) và (2) suy ra:

$\frac{AM}{AN}=\frac{DM}{DN}$  ( đpcm).

Bài 45 trang 80 Toán 8 Tập 2: Hai tam giác ABC và DEF có $\widehat{A}=\widehat{D};\widehat{B}=\widehat{E};$ AB = 8cm, BC = 10cm, DE = 6cm. Tính độ dài các cạnh AC, DF và EF, biết rằng cạnh AC dài hơn cạnh DF là 3cm.

Lời giải:

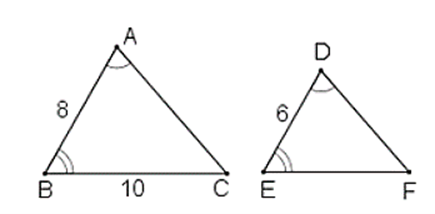
Xét ∆ABC và ∆DEF có:

$\begin{array}{l}\widehat{A}=\widehat{D}\\ \widehat{B}=\widehat{E}\end{array}$

Suy ra: ∆ABC $~$ ∆DEF (g.g).

Suy ra: $\frac{AB}{DE}=\frac{BC}{EF}=\frac{CA}{FD}$

hay $\frac{8}{6}=\frac{10}{EF}=\frac{CA}{DF}$

$\Rightarrow EF=\frac{6.10}{8}=7,5cm$

Lại có: 

$$\begin{gathered} \frac{CA}{DF}=\frac{8}{6} \\ \Rightarrow \frac{CA}{8}=\frac{DF}{6} \end{gathered}$$

Mà cạnh AC dài hơn cạnh DF là 3 cm nên:

AC – DF = 3

Theo tính chất của dãy tỉ số bằng nhau ta có:

$$\begin{gathered} \frac{CA}{8}=\frac{DF}{6} \\ =\frac{CA-\text{\hspace{0.17em}\hspace{0.17em}}DF}{8-6}=\frac{3}{2} \end{gathered}$$

Suy ra: 

$CA\text{\hspace{0.17em}\hspace{0.17em}}=8.\frac{3}{2}=12;D\text{}F=6.\frac{3}{2}=9cm$

Vậy CA = 12 cm; DF = 9cm;  EF = 7,5cm.