Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh bộ câu hỏi trắc nghiệm Toán lớp 8: Trường hợp đồng dạng thứ ba có đáp án chi tiết, chọn lọc. Tài liệu gồm 30 câu hỏi trắc nghiệm cực hay bám sát chương trình sgk Toán 8. Hi vọng với bộ câu hỏi trắc nghiệm Trường hợp đồng dạng thứ ba có đáp án này sẽ giúp bạn ôn luyện kiến thức để đạt kết quả cao trong bài thi môn Toán 8 sắp tới.
Giới thiệu về tài liệu:
- Số câu hỏi trắc nghiệm: 30 câu
- Lời giải & đáp án: có
Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu Trắc nghiệm Trường hợp đồng dạng thứ ba có đáp án – Toán lớp 8:

Bài 7: Trường hợp đồng dạng thứ ba
Bài 1: Cho tam giác ABC cân tại A. Trên cạnh AC lấy điểm M, trên đoạn thẳng BM lấy điểm K sao cho góc BCK = góc ABM.
1. Tam giác MBC đồng dạng với tam giác
A. MCK
B. MKC
C. KMC
D. CMK
Lời giải
Tam giác ABC cân tại A nên góc ABC = góc ACB, ta lại có B1 = C1 (gt) nên B2 = C2.
ΔMBC và ΔMCK có:
BMC là góc chung;
B2 = C2 (cmt)
Do đó ΔMBC ~ ΔMCK (g.g).
Đáp án cần chọn là: A
2. Tính MB.MK bằng
A. 2MC2
B. CA2
C. MC2
D. BC2
Lời giải
Vì ΔMBC ~ ΔMCK nên 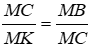
Suy ra MC2 = MB.MK
Đáp án cần chọn là: C
Bài 2: Cho ΔABC có các đường cao BD và CE cắt nhau tại H. Gọi M là giao của AH với BC.
1. Chọn câu đúng.
A. ΔHBE ~ ΔHCD
B. ΔABD ~ ΔACE
C. Cả A, B đều đúng
D. Cả A, B đều sai
Lời giải
Xét ΔHBE và ΔHCD có:
góc BDC = góc CEB = 900
góc EHB = góc DHC (2 góc đối đỉnh)
⇒ ΔHBE ~ ΔHCD (g - g)
Xét ΔABD và ΔACE có
góc AEC = góc BDA = 900
Góc A chung
Nên ΔABD ~ ΔACE (g - g)
Đáp án cần chọn là: C
2. Chọn khẳng định sai.
A. góc HDE = góc HCB
B. góc AMB = 900
C. góc HDE = góc HAE
D. góc HDE = góc HAD
Bài 3: Cho ΔABC có đường cao AD, CE và trực tâm H.
1. Chọn câu trả lời đúng nhất.
A. ΔADB ~ ΔCDH
B. ΔABD ~ ΔCBE
C. Cả A, B đều đúng
D. Cả A, B đều sai
Lời giải
Xét tam giác ABD và CBE có:
E = D = 900
Chung B
⇒ ΔABD ~ ΔCBE (g - g)
⇒ góc BAD = góc BCE = góc DCH (góc t/ư)
Xét ΔADB và ΔCDH có:
góc ADB = góc CDH = 900
góc BAD = góc DCH (cmt)
⇒ ΔADB ~ ΔCDH (g - g)
Vậy A, B đều đúng
Đáp án cần chọn là: C
2. Chọn khẳng định sai.
Lời giải
Đáp án cần chọn là: C
Bài 4: Cho hình bình hành ABCD, điểm F trên cạnh BC. Tia AF cắt BD và DC lần lượt ở E và G. Chọn khẳng định sai.
A. ΔBFE ~ ΔDAE
B. ΔDEG ~ ΔBEA
C. ΔBFE ~ ΔDEA
D. ΔDGE ~ ΔBAE
Lời giải
Có ABCD là hình bình hành nên: AD // BC, AB // DC
⇒ góc ADE = góc FBE (cặp góc so le trong)
⇒ góc ABE = góc EDG (cặp góc so le trong)
Xét tam giác BFE và tam ggiacs DAE có:
góc ADE = góc FBE (cmt)
góc AED = góc FEB (đối đỉnh)
⇒ ΔBFE ~ ΔDAE (g - g) nên A đúng, C sai.
Xét tam giác DGE và tam giác BAE có:
góc ABE = góc EDG (cmt)
góc AEB = góc GED (đối đỉnh)
⇒ ΔDGE ~ ΔBAE (g - g) hay ΔDEG ~ ΔBEA nên B, D đúng
Đáp án cần chọn là: C
Bài 5: Cho hình bình hành ABCD có I là giao điểm của AC và BD. E là một điểm bất kì thuộc BC, qua E kẻ đường thẳng song song với AB và cắt BD, AC, AD tại G, H, F. Chọn kết luận sai?
A. ΔBGE ~ ΔHGI
B. ΔGHI ~ ΔBAI
C. ΔBGE ~ ΔDGF
D. ΔAHF ~ ΔCHE
Lời giải
Có ABCD là hình bình hành nên: AD // BC, AB // DC
Xét ΔBGE và ΔDGF có:
● góc BGE = góc DGF (đối đỉnh)
● góc EBG = góc FDG (so le trong)
⇒ ΔBGE ~ ΔDGF (g-g) nên C đúng
Xét ΔAHF và ΔCHE có:
● góc AHF = góc CHE (đối đỉnh)
● góc HAF = góc HCE (so le trong)
⇒ ΔAHF ~ ΔCHE (g-g) nên D đúng
Lại có GH // AB ⇒ IHG = IAB (đồng vị)
Xét ΔGHI và ΔBAI có
● Chung I
● góc IHG = góc IAB (cmt)
⇒ ΔGHI ~ ΔBAI (g-g)
Suy ra B đúng
Chỉ có A sai.
Đáp án cần chọn là: A
Bài 6: Cho 2 tam giác ABC và DEF có A = 400, B = 800, E = 400, D = 600.
Chọn câu đúng.
A. ΔABC ~ ΔDEF
B. ΔFED ~ ΔCBA
C. ΔACB ~ ΔEFD
D. ΔDFE ~ ΔCBA
Lời giải
Xét ΔABC có: A + B + C = 1800 ⇒ C = 1800 - 400 - 800 = 600
Tam giác DEF có: D + E + F = 1800 ⇒ F = 1800 - D - E = 1800 - 400 - 600 = 800.
Xét ΔABC và ΔFED có:
● A = E = 400
● C = D = 600
⇒ ΔABC ~ ΔEFD (g - g) hay ΔCBA ~ ΔDFE
Đáp án cần chọn là: D
Bài 7: Cho ΔABC có các đường cao BD và CE cắt nhau tại H. Gọi M là giao của AH với BC.
1. Chọn câu đúng.
A. ΔHBE ~ ΔHCD
B. ΔABD ~ ΔACE
C. Cả A, B đều đúng
D. Cả A, B đều sai
Lời giải
Xét ΔHBE và ΔHCD có:
góc BDC = góc CEB = 900
góc EHB = góc DHC (2 góc đối đỉnh)
⇒ ΔHBE ~ ΔHCD (g - g)
Xét ΔABD và ΔACE có
góc AEC = góc BDA = 900
Góc A chung
Nên ΔABD ~ ΔACE (g - g)
Đáp án cần chọn là: C
2. Chọn khẳng định sai.
A. góc HDE = góc HCB
B. góc AMB = 900
C. góc HDE = góc HAE
D. góc HDE = góc HAD
Lời giải
góc EHD = góc HAE (hai góc đối đỉnh)
góc HDE = góc HAE
⇒ ΔHED ~ ΔHBC (c - g - c)
⇒ góc HDE = góc HCB (1)
Mà đường cao BD và CE cắt nhau tại H (theo giả thiết)
⇒ H là trực tâm của ΔABC
⇒ AH ⊥ BC tại M ⇒ AMB = 900
Xét ΔAMB và ΔCEB có:
góc CEB = góc AMB = 900
B chung
⇒ ΔAMB ~ ΔCEB (g - g)
⇒ góc MAB = góc ECB hay góc HAE = góc HCB (2)
Từ (1) và (2) ta có: góc HDE = góc HAE nên A, B, C đúng, D sai.
Đáp án cần chọn là: D
Bài 8: Cho ΔABC có đường cao AD, CE và trực tâm H.
1. Chọn câu trả lời đúng nhất.
A. ΔADB ~ ΔCDH
B. ΔABD ~ ΔCBE
C. Cả A, B đều đúng
D. Cả A, B đều sai
Lời giải
Xét tam giác ABD và CBE có:
E = D = 900
Chung B
⇒ ΔABD ~ ΔCBE (g - g)
⇒ góc BAD = góc BCE = góc DCH (góc t/ư)
Xét ΔADB và ΔCDH có:
góc ADB = góc CDH = 900
góc BAD = góc DCH (cmt)
⇒ ΔADB ~ ΔCDH (g - g)
Vậy A, B đều đúng
Đáp án cần chọn là: C
2. Chọn khẳng định sai.
Lời giải
Đáp án cần chọn là: C
Bài 9: Cho hình bình hành ABCD, điểm F trên cạnh BC. Tia AF cắt BD và DC lần lượt ở E và G. Chọn khẳng định sai.
A. ΔBFE ~ ΔDAE
B. ΔDEG ~ ΔBEA
C. ΔBFE ~ ΔDEA
D. ΔDGE ~ ΔBAE
Lời giải
Có ABCD là hình bình hành nên: AD // BC, AB // DC
⇒ góc ADE = góc FBE (cặp góc so le trong)
⇒ góc ABE = góc EDG (cặp góc so le trong)
Xét tam giác BFE và tam ggiacs DAE có:
góc ADE = góc FBE (cmt)
góc AED = góc FEB (đối đỉnh)
⇒ ΔBFE ~ ΔDAE (g - g) nên A đúng, C sai.
Xét tam giác DGE và tam giác BAE có:
góc ABE = góc EDG (cmt)
góc AEB = góc GED (đối đỉnh)
⇒ ΔDGE ~ ΔBAE (g - g) hay ΔDEG ~ ΔBEA nên B, D đúng
Đáp án cần chọn là: C
Bài 10: Cho hình bình hành ABCD có I là giao điểm của AC và BD. E là một điểm bất kì thuộc BC, qua E kẻ đường thẳng song song với AB và cắt BD, AC, AD tại G, H, F. Chọn kết luận sai?
A. ΔBGE ~ ΔHGI
B. ΔGHI ~ ΔBAI
C. ΔBGE ~ ΔDGF
D. ΔAHF ~ ΔCHE
Lời giải
Có ABCD là hình bình hành nên: AD // BC, AB // DC
Xét ΔBGE và ΔDGF có:
● góc BGE = góc DGF (đối đỉnh)
● góc EBG = góc FDG (so le trong)
⇒ ΔBGE ~ ΔDGF (g-g) nên C đúng
Xét ΔAHF và ΔCHE có:
● góc AHF = góc CHE (đối đỉnh)
● góc HAF = góc HCE (so le trong)
⇒ ΔAHF ~ ΔCHE (g-g) nên D đúng
Lại có GH // AB ⇒ IHG = IAB (đồng vị)
Xét ΔGHI và ΔBAI có
● Chung I
● góc IHG = góc IAB (cmt)
⇒ ΔGHI ~ ΔBAI (g-g)
Suy ra B đúng
Chỉ có A sai.
Đáp án cần chọn là: A
Bài 11: Tam giác ABC có A = 2B, AB = 11cm, AC = 25cm. Tính độ dài cạnh BC.
A. 30cm
B. 20cm
C. 25cm
D. 15cm
Lời giải
Trên tia đối của tia AC lấy điểm D sao cho AD = AB.
Tam giác ABD cân tại A nên góc BAC = B1 + D = 2D.
Ta lại có góc BAC = 2B2 nên D = B2.
Xét ΔCBA và ΔCDB có C chung và D = B2.
Nên ΔCBA ~ ΔCDB (g-g) nên
Từ đó BC2 = 25.36 suy ra BC = 5.6 = 30(cm)
Đáp án cần chọn là: A
Bài 12: Tam giác ABC có A = 2B, AC = 16cm, BC = 20cm. Tính độ dài cạnh AB.
A. 18cm
B. 20cm
C. 15cm
D. 9cm
Lời giải
Trên tia đối của tia AC lấy điểm D sao cho AD = AB.
Tam giác ABD cân tại A nên góc BAC = B1 + D = 2D.
Ta lại có góc BAC = 2B2 nên D = B2.
Xét ΔCBA và ΔCDB có C chung và D = B2.
⇒ x = 25 - 16 = 9 (cm)
Vậy AB = 9cm
Đáp án cần chọn là: D
Bài 13: Cho ΔABC cân tại A, có BC = 2a, M là trung điểm BC, lấy D, E thuộc AB, AC sao cho góc DME = góc ABC.
1. Tính BD.CE bằng
A. 2a2
B. 3a
C. a2
D. 4a2
Lời giải
+ Ta có: góc DMC = góc DME + góc EMC
Mặt khác: góc DMC = góc ABC + góc BDM (góc ngoài tam giác)
Mà: góc DME = góc ABC (gt) nên BDM = EMC
+ Ta có: góc ABC = góc ACB (ΔABC cân tại A) và góc BDM = góc EMC (cmt)
⇒ ΔBDM ~ ΔCME (g - g)
⇒ 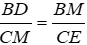
Lại có M là trung điểm của BC và BC = 2a ⇒ BM = MC = a
⇒ BD.CE = a2 không đổi
Đáp án cần chọn là: C
2. Góc BDM bằng với góc nào dưới đây?
A. DEM
B. MDE
C. ADE
D. AED
Lời giải
Đáp án cần chọn là: B
Bài 14: Cho tam giác ABC cân tại A, M là trung điểm của BC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho DM là tia phân giác của BDE.
1. Chọn khẳng định đúng.
A. góc ADE = góc AED
B. góc BDM = góc MEC
C. góc DEM = góc CEM
D. góc BMD = góc CME
Lời giải
Tam giác ABC có: M là trung điểm của BC nên AM vừa là đường trung tuyến vừa là đường phân giác trong góc A.
Lại có: DM là ghân giác của góc BDE nên DM là phân giác ngoài góc D của tam giác ADE.
Tam giác ADE có phân giác trong AM cắt phân giác ngoài DM tại M nên EM là đường phân giác ngoài góc E hay EM là phân giác của góc DEC.
Vậy góc DEM = góc CEM.
Đáp án cần chọn là: C
2. Chọn kết luận đúng.
A. ΔBDM ~ ΔCME
B. ΔBDM ~ ΔEMC
C. ΔBDM ~ ΔCEM
D. ΔBDM ~ ΔECM
Lời giải
Đặt B = C = x, góc BDM = góc EDM = y, góc CEM = góc DEM = z
Tứ giác BDCE có: B + C + BDE + CED = 3600
⇒ 2x + 2y + 2z = 3600 ⇔ x + y + z = 1800
Hay B + góc BDM + góc CEM = 1800
Mà B + góc BDM + góc BMD = 1800 (tổng ba góc trong tam giác)
Nên góc CEM = góc BMD
Xét ΔBDM và ΔCME có:
● B = C (gt)
● góc BMD = góc CEM (cmt)
⇒ ΔBDM ~ ΔCME (g - g)
Đáp án cần chọn là: A
Bài 15: Nếu 2 tam giác ABC và DEF có A = D, C = F thì:
A. ΔABC ~ ΔDEF
B. ΔCAB ~ ΔDEF
C. ΔABC ~ ΔDFE
D. ΔCBA ~ ΔDFE
Lời giải
Xét ΔABC và ΔDEF có:
● A = D (gt)
● C = F (gt)
⇒ ΔABC ~ ΔDEF (g - g)
Đáp án cần chọn là: A
Bài 16: Cho hai tam giác ABC và FED có A = F, cần thêm điều kiện gì dưới đây để hai tam giác (thứ tự đỉnh như vậy) đồng dạng theo trường hợp góc - góc?
A. B = E
B. C = E
C. B = F
D. C = F
Lời giải
Ta có: A = F, B = E thì ΔABC ~ ΔFED (g - g)
Đáp án cần chọn là: A
Bài 17: Cho hình bên biết AB = 6cm, AC = 9cm, góc ABD = góc BCA. Độ dài đoạn AD là:
A. 2cm
B. 3cm
C. 4cm
D. 5cm
Lời giải
Xét ΔABD và ΔACB có:
● A chung
● góc ABD = góc BCA (gt)
⇒ ΔABD ~ ΔACB (g-g)
Đáp án cần chọn là: C
Bài 18: Cho hình bên biết AB = 8cm, AC = 16cm, góc ABD = góc BCA. Độ dài đoạn AD là:
A. 4cm
B. 8cm
C. 6cm
D. 5cm
Lời giải
Xét ΔABD và ΔACB có:
● A chung
● góc ABD = góc BCA (gt)
⇒ ΔABD ~ ΔACB (g-g)
Đáp án cần chọn là: A
Bài 19: Nếu 2 tam giác ABC và DEF có A = 700, C = 600, E = 500, F = 700 thì chứng minh được:
A. ΔABC ~ ΔFED
B. ΔACB ~ ΔFED
C. ΔABC ~ ΔDEF
D. ΔABC ~ ΔDFE
Lời giải
Xét ΔABC có: A + B + C = 1800 ⇔ 700 + B + 600 = 1800
⇔ B = 1800 - 700 - 600 = 500
Xét ΔABC và ΔFED có:
A = F = 700
B = E = 500
⇒ ΔABC ~ ΔFED (g - g)
Đáp án cần chọn là: A
Bài giảng Toán 8 Bài 7: Trường hợp đồng dạng thứ ba