Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Bài 9: Hình chữ nhật hay, chi tiết giúp học sinh dễ dàng làm bài tập Hình chữ nhật lớp 8.

Giải bài tập Toán lớp 8 Bài 9: Hình chữ nhật

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 97 Toán 8 Tập 1: Chứng minh rằng hình chữ nhật ABCD trên hình 84 cũng là một hình bình hành, một hình thang cân.

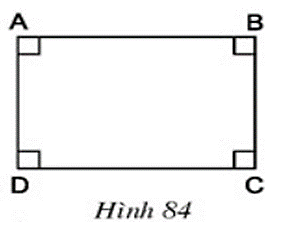
Lời giải

+) Hình chữ nhật ABCD có các góc đối bằng nhau (đều là góc vuông) nên ABCD là hình bình hành.

+) Vì $AD\perp AB,AD\perp D\text{}C\Rightarrow AB//DC$

Suy ra ABCD là hình thang

Mặt khác, ta có: $\widehat{C}=\widehat{D}={90}^0$

⇒ ABCD là hình thang cân

Câu hỏi 2 trang 98 Toán 8 Tập 1: Với một chiếc compa, ta sẽ kiểm tra được hai đoạn thẳng bằng nhau hay không bằng nhau. Bằng compa, để kiểm tra tứ giác ABCD có là hình chữ nhật hay không, ta làm thế nào ?

Lời giải

- Ta kiểm tra các cặp cạnh đối xem chúng có bằng nhau không

Nếu các cặp cạnh đối bằng nhau

⇒ ABCD là hình bình hành

- Sau đó: Kiểm tra hai đường chéo xem chúng bằng nhau không

Nếu hai đường chéo bằng nhau

⇒ ABCD là hình chữ nhật

Câu hỏi 3 trang 98 Toán 8 Tập 1: Cho hình 86:

a) Tứ giác ABDC là hình gì? Vì sao?

b) So sánh các độ dài AM và BC.

c) Tam giác vuông ABC có AM là đường trung tuyến ứng với cạnh huyền. Hãy phát biểu tính chất tìm được ở câu b) dưới dạng một định lý.

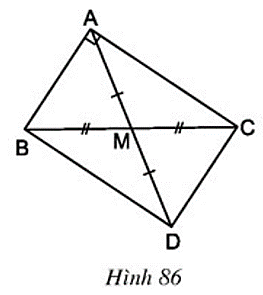
Lời giải

a) Tứ giác ABDC có hai đường chéo cắt nhau tại trung điểm mỗi đường

⇒ ABDC là hình bình hành

Hình bình hành ABDC có góc A vuông

⇒ ABDC là hình chữ nhật

b) Ta có AM = MD = $\frac{AD}{2}$ (M là trung điểm AD)

Vì ABDC là hình chữ nhật ⇒ AD = BC (hai đường chéo)

AM = MD =  $\frac{AD}{2}=\frac{BC}{2}.$

Vậy $AM=\frac{BC}{2}.$

c) Định lí được phát biểu như sau: Trong một tam giác vuông, trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền

Câu hỏi 4 trang 98 Toán 8 Tập 1: Cho hình 87:

a) Tứ giác ABDC là hình gì? Vì sao?

b) Tam giác ABC là tam giác gì?

c) Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. Hãy phát biểu tính chất tìm được ở câu b) dưới dạng một định lý.

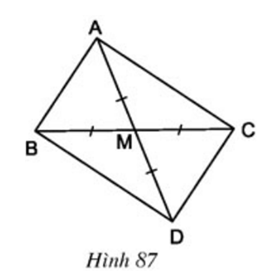
Lời giải

a) Tứ giác ABDC có hai đường chéo cắt nhau tại trung điểm mỗi đường

⇒ ABDC là hình bình hành

Hình bình hành ABDC có hai đường chéo AD và BC bằng nhau

⇒ ABDC là hình chữ nhật

b) ABDC là hình chữ nhật

⇒$\widehat{BAC}={90}^0$

⇒ ΔABC là tam giác vuông tại A

c) Định lí: Tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác đó là tam giác vuông

Bài tập (trang 99, 100)

Bài 58 trang 99 Toán 8 Tập 1: Điền vào chỗ trống, biết rằng a, b là độ dài của các cạnh, d là độ dài đường chéo của một hình chữ nhật.

Lời giải:

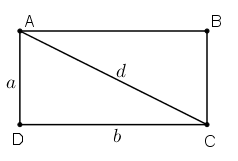
Trong hình chữ nhật ABCD ta luôn có

 $\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}={90}^0$

Xét tam giác vuông ADC, có:

AC² = AB² + BC²

⇒ d² = a² + b² (định lý Py – ta – go)

Với a = 5, b = 12

$$\begin{gathered} \Rightarrow d^2=5^2+{12}^2 \\ \Rightarrow d=\sqrt{5^2+{12}^2}=\sqrt{169}=13 \end{gathered}$$

Với $b=\sqrt{6},d=\sqrt{10}$

$$\begin{gathered} \Rightarrow {\left(\sqrt{10}\right)}^2=a^2+{\left(\sqrt{6}\right)}^2 \\ \Rightarrow 10=a^2+6 \\ \Rightarrow a^2=10-6=4 \\ \Rightarrow a=\sqrt{4}=2 \end{gathered}$$

Với $a=\sqrt{13},d=7$

$$\begin{gathered} \Rightarrow 7^2={\left(\sqrt{10}\right)}^2+b^2 \\ \Rightarrow 49=13+b^2 \\ \Rightarrow b^2=49-13=36 \\ \Rightarrow b=\sqrt{36}=6 \end{gathered}$$

Vậy ta có bảng sau:

Bài 59 trang 99 Toán 8 Tập 1: Chứng minh rằng:

a) Giao điểm của hai đường chéo của hình chữ nhật là tâm đối xứng của hình chữ nhật đó.

b) Hai đường thẳng đi qua trung điểm hai cặp cạnh đối của hình chữ nhật là hai trục đối xứng của hình chữ nhật đó.

Lời giải:

a)

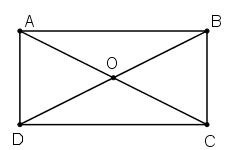
Giả sử ABCD là hình chữ nhật. Gọi O là giao điểm của AC và BD.

Theo tính chất đường chéo của hình chữ nhật ta có; hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.

Vậy: OA = OC và OB = OD

Do đó, O là tâm đối xứng của hình chữ nhật đó.

b)

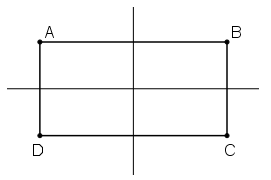
Cách 1: Áp dung tính chất: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.

ABCD là hình chữ nhật

⇒ ABCD là hình thang cân (hai đáy AB và CD)

⇒ Đường thẳng đi qua trung điểm AB và CD là trục đối xứng ABCD.

Tương tự vậy: ABCD cũng là hình thang cân với hai đáy AD và BC

⇒ Đường thẳng đi qua trung điểm AD và BC là trục đối xứng của ABCD.

Vậy ta có điều phải chứng minh.

Cách 2: Sử dụng đường trung bình:

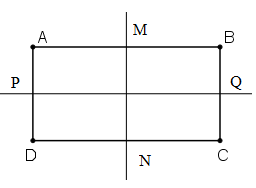
Vì ABCD là hình chữ nhật nên ABCD là hình thang

Ta có: M là trung điểm AB, N là trung điểm CD nên MN // AD // BC

Mà $AD\perp AB,AD\perp CD$

$\Rightarrow MN\perp AB,MN\perp CD$

Suy ra MN là trung trực của AB và CD.

Do đó A đối xứng với B qua MN, C đối xứng với D qua MN hay MN là trục đối xứng của hình chữ nhật ABCD.

Tương tự ta có PQ cũng là trục đối xứng của hình chữ nhật ABCD.

Bài 60 trang 99 Toán 8 Tập 1: Tính độ dài đường trung tuyến ứng với cạnh huyền của một tam giác vuông có cạch góc vuông bằng 7cm và 24 cm.

Lời giải:

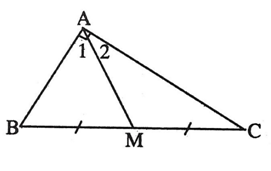
Gọi a là độ dài cạnh huyền của tam giác vuông.

Theo định lý Pi-ta-go ta có:

a² = 7² + 24² = 625

⇒ a = 25cm

⇒ Độ dài trung tuyến ứng với cạnh huyền bằng: $\frac{a}{2}=\frac{25}{2}=12,5$(cm).

Bài 61 trang 99 Toán 8 Tập 1: Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Tứ giác AHCE là hình gì? Vì sao?

Lời giải:

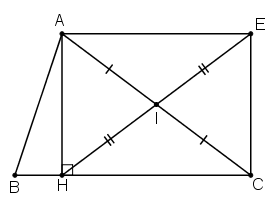
Ta có: I là trung điểm của AC

E đối xứng với H qua I  ⇒ IE = IH ⇒ I là trung điểm HE

Xét tứ giác AHCE, có

AC ∩ HE = {I} là trung điểm của AC và HE.

⇒ AHCE là hình bình hành (dấu hiệu nhận biết 4)

Ta lại có : $\widehat{H}={90}^0$

⇒ AHCE là hình chữ nhật (đpcm).

Bài 62 trang 99 Toán 8 Tập 1: Các câu sau đúng hay sai?

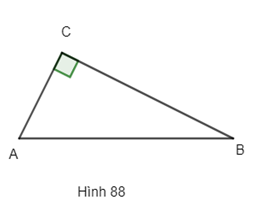
a) Nếu tam giác ABC vuông tại C thì điểm C thuộc đường tròn có đường kính là AB (h.88)

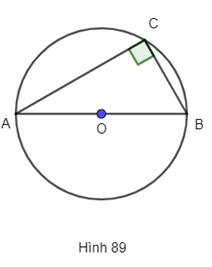
b) Nếu điểm C thuộc đường tròn có đường kính là AB (C khác A và B) thì tam giác ABC vuông tại C (h.89).

Lời giải:

a) Đúng

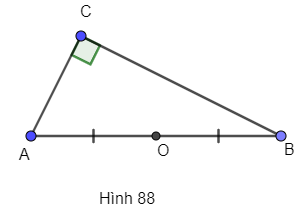
Gọi O là trung điểm của AB.

Ta có CO là trung tuyến ứng với cạnh huyền nên

⇒ $OC=\frac{AB}{2}=OA=OB$.

A, B, C cùng thuộc đường tròn tâm O bán kính OA.

Tâm O là trung điểm của AB nên AB là đường kính.

Vậy C thuộc đường tròn đường kính AB.

b) Đúng

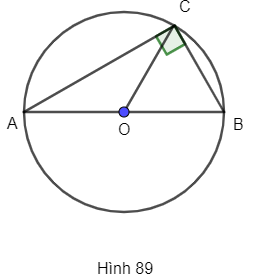
Vì A, B, C thuộc đường tròn tâm O.

⇒ OA = OB = OC = R

AB là đường kính nên AB = 2R.

Xét tam giác ABC có:

CO là trung tuyến và CO = $\frac{AB}{2}$.

⇒ ΔABC vuông tại C.

Bài 63 trang 100 Toán 8 Tập 1: Tìm x trên hình 90

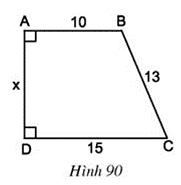
Lời giải:

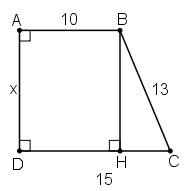
* Kẻ BH vuông góc CD.

Xét tứ giác ABHD có: $\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}={90}^0$

Suy ra tứ giác ABHD là hình chữ nhật

$\Rightarrow$ AB = DH = 10 ( hình chữ nhật có các cạnh đối bằng nhau)

+ Suy ra: HC = DC - DH = 15 – 10 = 5

+ Xét tam giác vuông BHC có:

BC² = BH² + HC² (định lý Py – ta – go)

⇔ 13² = BH² + 5²

⇔ BH² = 13² – 5² = 144

⇔ BH = 12

+ Do ABHD là hình chữ nhật nên AD = BH = 12

Vậy x = 12.

Bài 64 trang 100 Toán 8 Tập 1: Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.

Lời giải:

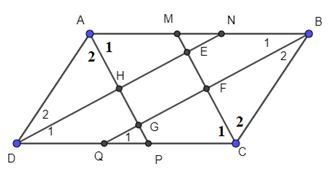
Gọi M, N, P, Q lần lượt là giao điểm của các đường phân giác với các cạnh của hình bình hành.

Ta có: $\widehat{D_1}=\widehat{D_2}=\frac{\widehat{ADC}}{2}$ (DN là phân giác $\widehat{ADC}$)

$\widehat{B_1}=\widehat{B_2}=\frac{\widehat{ABC}}{2}$ (BQ là phân giác $\widehat{ABC}$)

Mà $\widehat{ADC}=\widehat{ABC}$(hai góc đối của hình bình hành ABCD)

$\Rightarrow \widehat{D_1}=\widehat{B_1}$

Vì ABCD là hình bình hành AB // CD $\Rightarrow \widehat{Q_1}=\widehat{B_1}$ (hai góc so le trong)

$\Rightarrow \widehat{D_1}=\widehat{Q_1}$

Mà hai góc ở vị trí đồng vị

$\Rightarrow$DN // BQ hay HE // GF

Ta có: $\widehat{A_1}=\widehat{A_2}=\frac{\widehat{DAB}}{2}$ (AP là phân giác $\widehat{DAB}$)

$\widehat{C_1}=\widehat{C_2}=\frac{\widehat{DCB}}{2}$ (CM là phân giác $\widehat{DCB}$)

Mà $\widehat{DAB}=\widehat{DCB}$(hai góc đối của hình bình hành ABCD)

$\Rightarrow \widehat{A_1}=\widehat{C_1}$

Vì ABCD là hình bình hành AB // CD $\Rightarrow \widehat{A_1}=\widehat{QPG}$ (hai góc so le trong)

$\Rightarrow \widehat{C_1}=\widehat{QPB}$

$\Rightarrow$AP //DM hay GH // EF

Xét tứ giác EFGH có:

HE // GF (cmt)

GH // EF (cmt)

$\Rightarrow$EFGH là hình bình hành (1)

Xét tam giác BFC, có:

$\widehat{B_2}+\widehat{C_2}=\frac{\widehat{ABC}}{2}+\frac{\widehat{BCD}}{2}=\frac{\widehat{ABC}+\widehat{BCD}}{2}$

Mà $\widehat{ABC}+\widehat{BCD}=180°$ (hai góc trong cùng phía bù nhau)

$\Rightarrow \widehat{B_2}+\widehat{C_2}=\frac{180°}{2}=90°$

$\Rightarrow \widehat{BFC}=180°-\left(\widehat{B_2}+\widehat{C_2}\right)=90°$ hay $\Rightarrow \widehat{EFG}=90°$(2)

Từ (1) và (2) suy ra tứ giác EFGH là hình chữ nhật.

Bài 65 trang 100 Toán 8 Tập 1: Tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?

Lời giải:

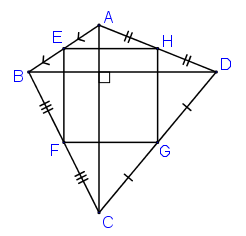
Xét ΔABC, có:

E là trung điểm của AB (gt)

F là trung điểm của BC (gt)

⇒ EF là đường trung bình của ΔABC

⇒EF // AC và $\text{EF}=\frac{AC}{2}$ (1)

Xét ΔADC, có:

H là trung điểm của AD (gt)

G là trung điểm của DC (gt)

⇒ HG là đường trung bình của ΔADC

⇒ HG // AC và $HG=\frac{AC}{2}$ (2)

Từ (1) và (2) suy ra EF // HG và EF = HG

⇒ Tứ giác EFGH là hình bình hành (*)

Ta có: EF // AC

Mà $AC\perp BD$

$\Rightarrow EF\perp BD$ (3)

Xét ΔABD, có:

E là trung điểm của AB

H là trung điểm của AD

⇒ EH là đường trung bình của ΔABD

⇒ EH // BD (4)

Từ (3) và (4) suy ra $EF\perp EH\Rightarrow \widehat{FEH}=90°$ (**)

Từ (*) và (**) suy ra EFGH là hình chữ nhật.

Bài 66 trang 100 Toán 8 Tập 1: Đố. Một đội công nhân đang trồng cây trên đoạn đường AB thì gặp chướng ngại vật che lấp tầm nhìn (h.92). Đội đã dựng các điểm C, D, E như trên hình vẽ rồi trồng cây tiếp trên đoạn đường EF vuông góc với DE. Vì sao AB và EF cùng nằm trên một đường thẳng?

Lời giải:

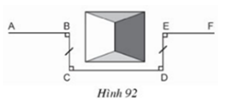
Tứ giác BCDE có:

BC // DE (vì cùng vuông góc với CD);

BC = DE

nên BCDE là hình bình hành ⇒ CD // BE (1)

Ta có:

$\left.\begin{array}{l}AB\perp BC\\ CD\perp BC\end{array}\right\}\Rightarrow AB//CD$ (2)

Ta lại có:

$\left.\begin{array}{l}\text{EF}\perp ED\\ CD\perp ED\end{array}\right\}\Rightarrow \text{EF}//CD$ (3)

Từ (1), (2) và (3) theo tiên đề Ơ-clit suy ra A, B, E, F thẳng hàng.