Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Bài 5: Dựng hình bằng thước và compa. Dựng hình thang hay, chi tiết giúp học sinh dễ dàng làm bài tập Dựng hình bằng thước và compa. Dựng hình thang lớp 8.

Giải bài tập Toán lớp 8 Bài 5: Dựng hình bằng thước và compa. Dựng hình thang

Bài tập (trang 83)

Bài 29 trang 83 Toán 8 Tập 1: Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 4cm, góc nhọn $\widehat{B}=65°$.

Lời giải

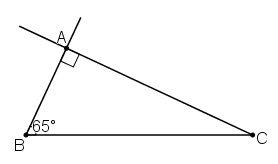
a) Phân tích

Giả sử dựng được ΔABC thỏa mãn yêu cầu đề bài.

Đoạn thẳng BC dựng được vì đã biết độ dài.

Khi đó điểm A là giao điểm của:

+ Tia Bx tạo với đoạn thẳng BC góc 65º

+ Đường thẳng qua C và vuông góc với tia Bx vừa dựng.

b) Cách dựng:

- Dựng đoạn thẳng BC = 4cm.

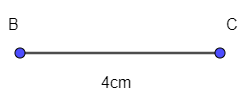
- Dựng tia Bx tạo với BC một góc 65º.

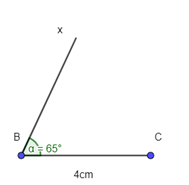
- Dựng đường thẳng a qua C và vuông góc với Bx.

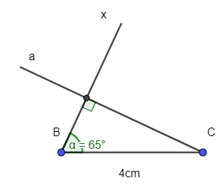
- Bx cắt a tại A.

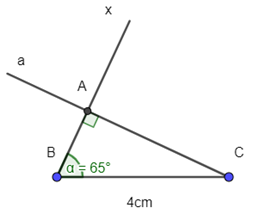
ΔABC là tam giác cần dựng.

c) Chứng minh: ΔABC vừa dựng vuông tại A, góc B = 65º và BC = 4cm.

d) Biện luận: Ta luôn dựng được một tam giác thỏa mãn điều kiện đề bài.

Bài 30 trang 83 Toán 8 Tập 1: Dựng tam giác ABC vuông tại B, biết cạnh huyền AC = 4cm, cạnh góc vuông BC = 2cm.

Lời giải

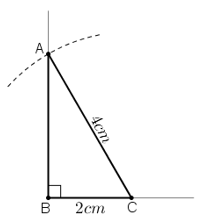
a) Phân tích:

Giả sử dựng được ΔABC thỏa mãn yêu cầu.

Ta dựng được đoạn BC vì biết BC = 2cm.

Khi đó điểm A là giao điểm của:

+ Tia Bx vuông góc với BC

+ Cung tròn tâm C bán kính 4cm.

b) Cách dựng:

+ Dựng đoạn thẳng BC = 2cm:

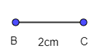
+ Dựng tia Bx vuông góc với cạnh BC:

+ Dựng cung tròn tâm C, bán kính 4cm. Cung tròn cắt tia Bx tại A:

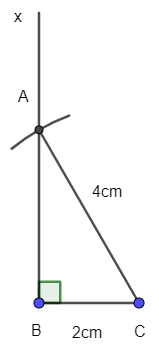
Kẻ AC ta được ΔABC cần dựng.

c) Chứng minh

ΔABC có góc B = 90º, BC = 2cm.

A thuộc cung tròn tâm C bán kính 4cm nên AC = 4cm.

Vậy ΔABC thỏa mãn yêu cầu đề bài

d) Biện luận: Ta luôn dựng được một tam giác thỏa mãn điều kiện của đề bài.

Bài 31 trang 83 Toán 8 Tập 1: Dựng hình thang ABCD (AB // CD), biết AB = AD = 2cm, AC = DC = 4cm.

Lời giải

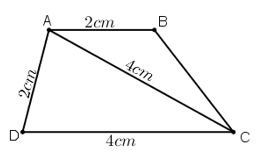
a) Phân tích :

Giả sử dựng được hình thang ABCD thỏa mãn yêu cầu đề bài.

Tam giác ADC dựng được vì biết ba cạnh của tam giác.

Điểm B phải thỏa mãn hai điều kiện :

+ B nằm trên tia Ax song song với CD

+ B cách A một đoạn 2cm.

b) Cách dựng:

+ Dựng tam giác ADC có AD = 2cm, AC = 4cm, CD = 4cm.

- Vẽ đoạn CD = 4cm:

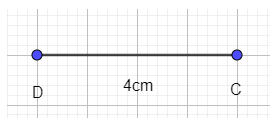
- Vẽ cung tròn tâm C bán kính 4cm và cung tròn tâm D bán kính 2 cm. Hai cung tròn này cắt nhau tại A.

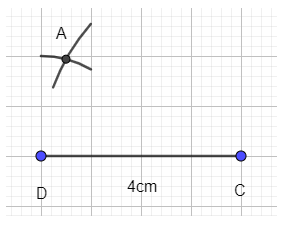
- Nối A với D và A với C ta được tam giác ACD

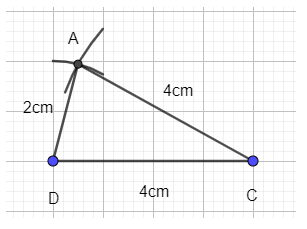
+ Dựng tia Ax song song với CD và nằm trên cùng một nửa mặt phẳng chứa điểm C bờ là đường thẳng AD.

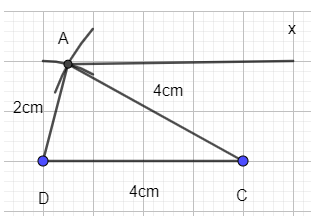
+ Trên tia Ax lấy điểm B sao cho AB = 2cm.

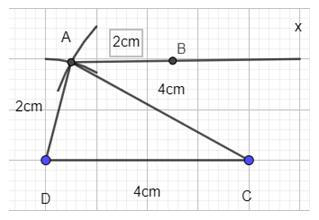
Kẻ BC ta được hình thang ABCD cần dựng.

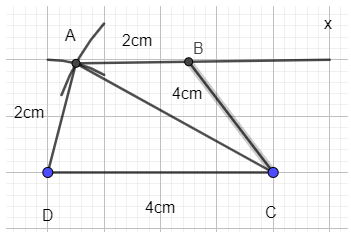
c) Chứng minh

Tứ giác ABCD là hình thang vì AB // CD.

Hình thang ABCD có AB = AD = 2cm, AC = BC = 4cm thỏa mãn yêu cầu đề bài

d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn yêu cầu của đề bài.

Bài 32 trang 83 Toán 8 Tập 1: Hãy dựng một góc bằng 30^o.

Lời giải

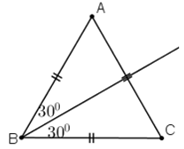
Nếu chỉ sử dụng thước thẳng và compa, ta sẽ dựng như sau:

a) Phân tích

Để dựng một góc 30º, ta dựng góc 60º rồi dựng tia phân giác của góc đó.

Để dựng góc 60º, ta dựng tam giác đều với độ dài cạnh bất kì.

b) Cách dựng:

- Dựng tam giác đều ABC với độ dài cạnh bất kì (ví dụ độ dài 2cm)

- Dựng tia phân giác Bx của góc $\widehat{ABC}$

Ta được góc $\widehat{ABx}=\widehat{CBx}=30°$

c) Chứng minh

ΔABC đều nên $\widehat{ABC}=60°$

Bx là tia phân giác của $\widehat{ABC}$ nên $\widehat{ABx}=\widehat{CBx}=\frac{\widehat{ABC}}{2}=\frac{60°}{2}=30°$

Vậy ta dựng được góc 30º thỏa mãn yêu cầu đề bài.

Nếu được sử dụng thước đo góc:

a) Phân tích:

Để dựng $\widehat{ABC}=30°$, ta sẽ dựng đoạn BC với độ dài bất kì, sau đó sử dụng thước đo góc dựng tia BA tạo với đoạn BC một góc $30°$.

b) Cách dựng:

- Dựng đoạn BC = 3cm

- Dùng thước đo góc dựng tia BA tạo với tia BC một góc $\widehat{ABC}=30°$.

Khi đó ta được:

c) Chứng minh:

Theo cách dựng ta được góc $\widehat{ABC}=30°$

Bài 33 trang 83 Toán 8 Tập 1: Dựng hình thang cân ABCD, biết đáy CD = 3cm, đường chéo AC = 4cm, góc $\widehat{D}=80°$.

Lời giải

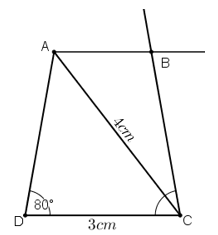
a) Phân tích

Giả sử dựng được hình thang ABCD theo yêu cầu đề bài.

Ta dựng được đoạn thẳng CD = 3cm.

Điểm A phải thỏa mãn hai điều kiện:

+ Tia DA tạo với DC một góc bằng 80º.

+ CA = 4cm nên A thuộc cung tròn tâm C bán kính 4cm.

ABCD là hình thang nên AB // CD

Mà hình thang ABCD cân nên $\widehat{BCD}=\widehat{D}=80°$ hoặc BD = AC = 4cm.

Vì vậy điểm B phải thỏa mãn 2 điều kiện:

+ B nằm trên đường thẳng đi qua A và song song với CD

+ Tia CB tạo với CD một góc 80º (hoặc nằm trên cung tròn tâm D bán kính 4cm).

b) Cách dựng

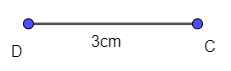
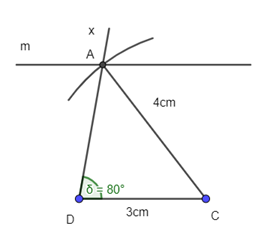
+ Dựng đoạn CD = 3cm:

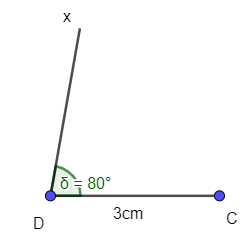
+ Dựng tia Dx thỏa mãn $\widehat{CDx}=80°$:

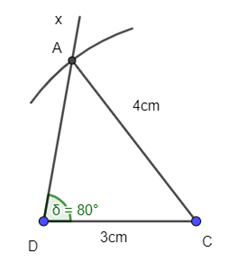
+ Dựng cung tròn tâm C, bán kính 4cm cắt tia Dx tại A.

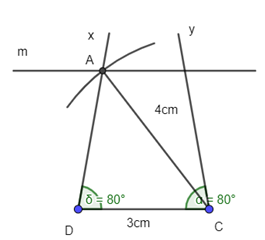
+ Qua A dựng đường thẳng m song song với CD:

+ Dựng tia Cy trên cùng nửa mặt phẳng chứa điểm A, bờ CD thỏa mãn $\widehat{DCy}=80°$

+ Tia Cy cắt đường thẳng m tại B.

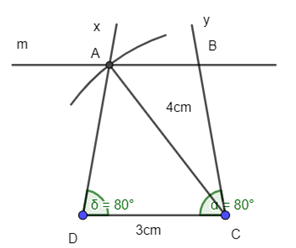
Hoặc vẽ cung tròn tâm D bán kính 4cm, cung tròn này cắt đường thẳng m tại B:

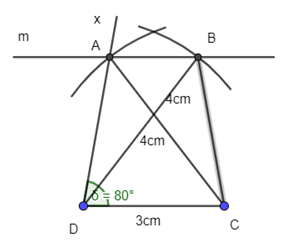
Ta dựng được hình thang ABCD

c) Chứng minh

+ Tứ giác ABCD là hình thang vì AB // CD

+ Hình thang ABCD có $\widehat{D}=\widehat{C}=80°$ nên là hình thang cân.

+ Hình thang cân ABCD có CD = 3cm, AC = 4cm, $\widehat{D}=80°$ nên thỏa mãn yêu cầu đề bài.

d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện đề bài.

Bài 34 trang 83 Toán 8 Tập 1: Dựng hình thang ABCD, biết $\widehat{D}=90°$, đáy CD = 3cm, cạnh bên AD = 2cm, cạnh bên BC = 3cm.

Lời giải

a) Phân tích

Giả sử dựng được hình thang ABCD thỏa mãn yêu cầu đề bài.

Ta dựng được tam giác ADC vì biết hai cạnh và góc xen giữa.

Điểm B phải thỏa mãn hai điều kiện:

+ B nằm trên đường thẳng qua A và song song với CD

+ CB = 3cm nên B thuộc cung tròn tâm C bán kính 3cm.

b) Cách dựng:

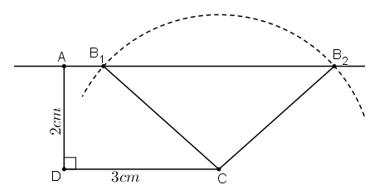
- Dựng tam giác ADC vuông tại D với DC = 3cm, DA = 2cm.

- Dựng tia Ax // CD (tia Ax về phía C).

- Dựng (C; 3cm) cắt tia Ax tại hai điểm B₁ và B₂.

Hình thang ABCD với B trùng với B₁ hoặc B trùng với B₂ là hình thang cần dựng.

c) Chứng minh: Theo cách dựng thì tứ giác ABCD hoặc AB₁CD có góc $\widehat{D}=90°$, đáy CD = 3cm, cạnh bên AD = 2cm, cạnh bên BC = 3cm nên đó là hình thang vuông thỏa mãn điều kiện đề bài.

d) Biện luận: Ta dựng được hai hình thang thỏa mãn điều kiện đề bài.