Tailieumoi.vn xin giới thiệu Tìm giá trị của m để hai đường thẳng song song, cắt nhau 2025 đầy đủ, chi tiết được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Hai đường thẳng song song, cắt nhau. Mời các bạn đón xem:
Tìm giá trị của m để hai đường thẳng song song, cắt nhau
A. Lý thuyết Tìm giá trị m để hai đường thẳng song song, cắt nhau
- Trong hệ trục tọa độ Oxy có hai đường thẳng y = ax + b (a ≠ 0) và y = a'x + b' (a' ≠ 0):
+ Hai đường thẳng này song song khi a = a', b ≠ b'.
+ Hai đường thẳng cắt nhau khi a ≠ a'.
+ Hai đường thẳng trùng nhau khi a = a', b = b'.
+ Hai đường thẳng vuông góc với nhau khi a . a' = ‒1.
B. Bài tập Tìm giá trị m để hai đường thẳng song song, cắt nhau
1. Bài tập trắc nghiệm
Câu 1: Hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0) cắt nhau khi
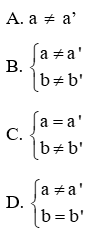
Lời giải:
Cho hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0)
d cắt d’ ⇔ a ≠ a’
Đáp án cần chọn là: A
Câu 2: Hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0) trùng nhau khi:
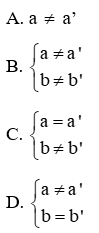
Lời giải:
Cho hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0)
d trùng d’ ó a=a’; b=b’
Đáp án cần chọn là: D
Câu 3: Hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0) có a = a’ và b ≠ b’. Khi đó:
A. d // d’
B. d ≡ d’
C. d cắt d’
D. d ⊥ d’
Lời giải:
Cho hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0)
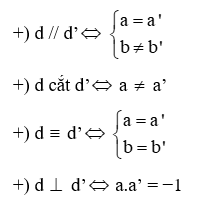
Đáp án cần chọn là: A
Câu 4: Hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0) có a ≠ a’. Khi đó:
A. d // d’
B. d ≡ d’
C. d cắt d’
D. d ⊥ d’
Lời giải:
Cho hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0)
+) d cắt d’ ⇔ a ≠ a’
Đáp án cần chọn là: C
Câu 5: Cho hai đường thẳng d: y = x + 3 và d’: y = −2x. Khi đó:
A. d // d’
B. d ≡ d’
C. d cắt d’
D. d ⊥ d’
Lời giải:
Ta thấy d: y = x + 3 có a = 1 và d’: y = −2x có a’ = −2
⇒ a ≠ a’ (1 ≠ −2) nên d cắt d’
Đáp án cần chọn là: C
Câu 6: Cho hai đồ thị của hàm số bậc nhất là hai đường thẳng d: y = (m + 2)x – m và d’: y = −2x − 2m + 1. Với giá trị nào của m thì d cắt d’?
A. m ≠ −2
B. m ≠ −4
C. m ≠ {−2; −4}
D. m ≠ {2; −4}
Lời giải:
+) Ta thấy d: y = (m + 2)x – m có a = m + 2 và d’: y = −2x − 2m + 1 có a’ = −2
+) Để y = (m + 2)x – m là hàm số bậc nhất thì m + 2 ≠ 0 ⇔ m ≠ −2.
+) Để d cắt d’⇔ a ≠ a’
m + 2 ⇔ −2 ⇔ m −4
Vậy m ⇔ {−2; −4}
Đáp án cần chọn là: C
Câu 7: Cho hai đồ thị của hàm số bậc nhất là hai đường thẳng d: y = (3 – 2m)x – 2 và d’: y = 4x − m + 2. Với giá trị nào của m thì d cắt d’?
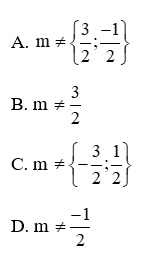
Lời giải:
Ta thấy d: y = (3 – 2m)x – 2 có a = 3 – 2m và d’: y = 4x − m + 2 có a’ = 4
Để d: y = (3 – 2m)x – 2 là hàm số bậc nhất thì 3 – 2m
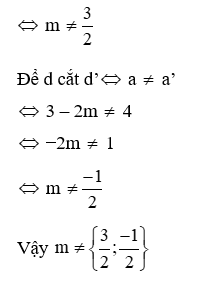
Đáp án cần chọn là: A
2. Bài tập tự luận
Bài 1: Cho hai hàm số y = kx + m -2 và y = (5 – k).x + (4 – m). Tìm m, k để đồ thị của hai hàm số:
a, Trùng nhau
b, Song song với nhau
c, Cắt nhau
Lời giải:
Để hàm số y = kx + m – 2 là hàm số bậc nhất khi k ≠0
Để hàm số y = (5 – k)x + (4 – m) là hàm số bậc nhất khi 5− k ≠0⇔ k ≠5
a, Để đồ thị của hai hàm số trùng nhau ⇔{k=5−k; m−2=4−m ⇔ {2k=5; 2m =6 ⇔ {k =5/ 2(t/m) ; m=3(t/m)
Vậy với k=5/2;m=3 thì đồ thị của hai hàm số trùng nhau
b, Để đồ thị của hai hàm số song song với nhau ⇔{k=5−k; m−2≠4−m ⇔ {k = 5/ 2; m≠3
Vậy với k=5/2;m≠3 thì đồ thị của hai hàm số song song với nhau
c, Để đồ thị của hai hàm số cắt nhau ⇔k ≠ 5−m⇔ 2k ≠ 5⇔ k ≠ 5/2
Vậy với k ≠ 5/2 thì hai đồ thị hàm số cắt nhau
Bài 2: Cho hàm số y = (2m – 3)x + m – 5. Tìm m để đồ thị hàm số:
a, Tạo với 2 trục tọa độ một tam giác vuông cân
b, Cắt đường thẳng y = 3x – 4 tại một điểm trên Oy
c, Cắt đường thẳng y = -x – 3 tại một điểm trên Ox
Lời giải:
Để hàm số là hàm số bậc nhất ⇔ 2m−3 ≠0⇔ m≠ 3/2
Gọi giao điểm của hàm số với trục Ox là A. Tọa độ của điểm A là A(5−m/2m−3;0)
Độ dài của đoạn OA=|5m/2m−3|
Gọi giao điểm của hàm số với trục Oy là B. Tọa độ của điểm B là B(0;m−5)
Độ dài của đoạn OB=|M−5|
Ta có tam giác OAB là tam giác vuông tại A
Để tam giác OAB là tam giác vuông cân ⇔|5−m/2m−3|=|m−5|⇔[m=1 hoặc m=2(t/m)
Vậy với m = 1 hoặc m = 2 thì đồ thị hàm số tạo với hai trục tọa độ tam giác vuông cân
b, Gọi A là điểm đồ thị hàm số cắt đường thẳng y = 3x – 4 tại một điểm trên trục Oy (trục tung) ⇒ A(0;b)
Thay tọa độ điểm A vào đồ thị hàm số y = 3x – 4 ta có b = 4
Điểm A(0; 4) thuộc đồ thị hàm số y = (2m – 3)x + m – 5 nên ta có
4=(2m−3).0+m−5⇔m−5=4⇔m=9(t/m)
Vậy với m = 9 thì đồ thị hàm số cắt đường thẳng y = 3x – 4 tại một điểm trên trục tung
c, Gọi B là điểm đồ thị hàm số cắt đường thẳng y = – x – 3 tại một điểm trên trục Ox (trục hoành) ⇒B(a;0)
Thay tọa độ điểm B vào đồ thị hàm số y = – x – 3 ta có a = – 3
Điểm B(-3; 0) thuộc đồ thị hàm số y = -x – 3 nên ta có:
0=(−3)(2m−3)+ m −5⇔−5m +4 = 0 ⇔ m =4/5 (t/m)
Vậy với m = 4/5 thì đồ thị hàm số cắt đường thẳng y = -x – 3 tại một điểm trên trục hoành
Bài 3: Cho hai đường thẳng (d1): y = (m + 1)x + 2 và (d2): y = 2x + 1. Tìm m để hai đường thẳng cắt nhau tại một điểm có hoành độ và tung độ trái dấu
Lời giải:
Để hai đường thẳng cắt nhau thì m+1≠2 ⇔ m≠1
Phương trình hoành độ giao điểm:
(m+1)x+2 = 2x+1
⇔mx + x + 2 = 2x+1
⇔x(m+1−2)=−1
⇔x(m−1)=−1
⇒x=−1/m−1
Với x=−1/m−1 ⇒y=2.(−1/m−1)+1=m−3/m−1
Để hoành độ và tung độ trái dấu thì x.y < 0
⇔−1/m−1.m−3/m−1<0⇔3−m(m−1)^2<0 (tử và mẫu trái dấu)
Mà (m−1)^2 ≥ 0∀ m≠1 ⇒ 3−m<0 ⇔ m>3
Vậy với m > 3 thì hai đường thẳng cắt nhau tại một điểm có hoành độ và tung độ trái dấu
Bài 4: Tìm m để đồ thị của hàm số y = (m – 2)x + m + 3 và các đồ thị của các hàm số y = -x + 2 và y = 2x – 1 đồng quy
Lời giải:
Gọi A là giao điểm của đồ thị hàm số y = -x + 2 và y = 2x – 1. Khi đó tọa độ của điểm A là nghiệm của hệ phương trình: 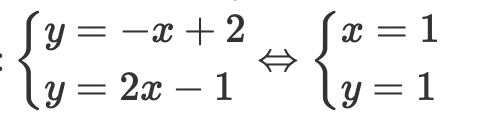
Vậy A(1; 1)
Ba đường thẳng đồng quy nên đồ thị hàm số y = (m – 2)x + m + 3 đi qua điểm A(1; 1)
Thay tọa độ điểm A vào phương trình ta có: 1 = 1.(m – 2) + m + 3 hay m = 0
Vậy với m = 0 thì ba đường thẳng đồng quy
3. Bài tập tự luyện
Bài 1: Cho hàm số y = 2x + 3k và y = (2m + 1)x + 2l – 3. Tìm điều kiện của m và k để đồ thị của hai hàm số là:
a, Hai đường thẳng cắt nhau
b, Hai đường thẳng song song với nhau
c, Hai đường thẳng trùng nhau
Bài 2: Cho hàm số y = mx + 4 và y = (2m – 3)x – 2. Tìm m để đồ thị của hai hàm số đã cho là:
a, Hai đường thẳng song song với nhau
b, Hai đường thẳng cắt nhau
c, Hai đường thẳng trùng nhau
d, Hai đường thẳng cắt nhau tại 1 điểm trên trục tung
Bài 3: Cho hai hàm số y = 2x + m – 3 và y = 5x + 5 – 3m. Tìm m để đồ thị của hai hàm số trên cắt nhau tại một điểm trên trục tung
Bài 4: Cho hai hàm số y = (m – 1)x + 3 và y = (3 – m)x + 1
a, Với giá trị nào của m thì đồ thị của hai hàm só là hai đường thẳng song song với nhau
b, Với giá trị nào của m thì đồ thị của 2 hàm số là hai đường thẳng cắt nhau
Bài 5: Cho hàm số y = mx – 2 (m khác 0). Xác định giá trị của m để đồ thị hàm số cắt hai trục tọa độ tạo thành tam giác có diện tích bằng 1.
Bài 6: Cho hàm số y = x + m. Tìm m để đồ thị hàm số song song với đường thẳng x – y + 3 = 0
Bài 7: Tìm m để đường thẳng y = x + m2 + 1 và đường thẳng y = 5 + (m – 1)x cắt nhau tại
a, Một điểm trên trục hoành
b, Một điểm trên trục tung
Bài 8: Cho hai hàm số bậc nhất y = (m – 1)x + 3 và y = (3 – m)x + 1
a, Với giá trị nào của m thì đồ thị của hai hàm số là hai đường thẳng song song với nhau
b, Với giá trị nào của m thì đồ thị của hai hàm số là hai đường thẳng cắt nhau
Bài 9: Cho đường thẳng (d1): y = x + 2 và đường thẳng (d2): y = -2x + 2
a, Tìm tọa độ giao điểm của (d1) và (d2) bằng phép tính
b, Gọi giao điểm của (d1) và (d2) với trục Ox lần lượt là A và B. Tính diện tích và chu vi của tam giác ABC
Bài 10: Cho hàm số y = (2m – 1)x + n. Tìm m và n để đồ thị hàm số trên song song với đường thẳng y = 2x và đi qua A (1; 2)