Tailieumoi.vn xin giới thiệu Cách chứng minh tiếp tuyến của một đường tròn lớp 9 hay, dễ hiểu được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết tiếp tuyến của một đường tròn. Mời các bạn đón xem:
Cách chứng minh tiếp tuyến của một đường tròn
A. Cách chứng minh tiếp tuyến của một đường tròn
Dấu hiệu nhận biết tiếp tuyến của một đường tròn
- Dấu hiệu 1: Khi một đường thẳng đi qua một điểm trên đường tròn và tạo ra một góc vuông với bán kính đi qua diểmđó thì ta có thể xác định rằng đường thẳng đó là tiếp tuyến của đường tròn tại điểm đó. Điều này đồng nghĩa với việc đường thẳng chạm vào đường tròn tại một điểm cụ thể và gặp bán kính tại điểm đó với góc 90 độ tức là đường thẳng này vuông góc với bán kính tại điểm tiếp xúc.
- Dấu hiệu 2: Tiếp tuyến của đường tròn có thể được xác định bằng cách mô tả tiếp điểm. Nếu một đường thẳng tạo ra một góc vuông với bán kính của đường trong và đi qua một điểm trên đường tròn, điểm đó sẽ được định nghĩa là tiếp điểm của đường thẳng với đường tròn. Điều này đồng nghĩa vơi việc đường thẳng không chỉ gặp đường tròn tại một điểm cụ thể mà còn tạo một góc vuông với bán kính tại điểm đó và điểm đó chính là tiếp điểm của đường thẳng với đường tròn.
Cách chứng minh tiếp tuyến của đường tròn:
- Cách 1: Để chứng minh đường thẳng d vuông góc với bán kính của đường tròn chúng ta có thể sử dụng tính chất của góc vuông trong tam giác vuông tạo bởi đường thẳng và bán kính. Bằng cách sử dụng định nghĩa của góc vuông và tính chất của tam giác vuông thì ta có thể chứng minh rằng đường thẳng d là tiếp tuyến của đường tròn.
- Cách 2: Để chứng minh khoảng cách từ tâm O của đường tròn đến đường thẳng d bằng bán kính R của đường tròn thì ta có thể sử dụng hình vẽ hình học và áp dụng định nghĩa của bán kính. KHoảng cách từ tâm O đến đường thẳng d sẽ bằng bán kính R của đường tròn.
- Cách 3: Để chứng minh hệ thức MA2 = MB. MC thì chúng ta có thể sử dụng định nghĩa của tiếp tuyến và hệ thức nối tiếp của các điểm trên đường tròn. Bằng cách áp dụng các quy tắc tam giác trong tam giác ADE ta có thể chứng minh rằng MA là tiếp tuyến của đường tròn ngoại tiếp tam giác ADE khi hệ thức trên được thỏa mãn.
B. Bài tập chứng minh tiếp tuyến của một đường tròn
1. Bài tập trắc nghiệm
Câu 1 : Cho nửa đường tròn tâm O đường kính AB. Ax, By là hai tiếp tuyến của (O) (Ax, By cùng phía đối với đường thẳng AB). Trên Ax lấy điểm C, trên By lấy điểm D sao cho
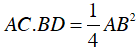
Khi đó:
a. CD tiếp xúc với đường tròn (O)
b. CD cắt đường tròn (O) tại hai điểm phân biệt
c. CD không có điểm chung với (O)
d. CD = R2
Hướng dẫn giải
Đáp án A
Trên tia đối của tia BD lấy điểm E sao cho BE = AC
Kẻ OH ⊥ CD
Ta có:
Mà AC = BE ⇒ BE.BD = R2 = OB2
⇒ ΔDOE vuông tại O
Xét ΔOAC và ΔOBE , ta có:
AC = BE (gt)
OA = OB (=R)
⇒ ΔOAC = ΔOBE (g-g-g)
⇈ 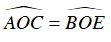
Ta có:
Nên C, O, E thẳng hàng
Xét tam giác DCE, có:
OD vừa là đường cao vừa là đường trung tuyến của △CDE nên OD cũng là đường phân giác.
⇒ 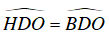
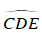
Xét ΔOHD và ΔOBD , có:
OD chung
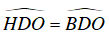
⇒ ΔOHD = ΔOBD (cạnh huyền - góc nhọn)
⇒ OH = OB ⇒ CD tiếp xúc với đường tròn (O).
Câu 2 : Cho tam giác ABC cân tại A, đường cao AH và BK cắt nhau ở I. Khi đó:
a. AK là tiếp tuyến của đường tròn đường kính AI
b. BK là tiếp tuyến của đường tròn đường kính AI
c. BH là tiếp tuyến của đường tròn đường kính AI
d. HK là tiếp tuyến của đường tròn đường kính AI
Hướng dẫn giải
Đáp án D
Gọi O là trung điểm của AI, khi đó: KO là đường trung tuyến của tam giác vuông AKO.
⇒ AO = IO = OK.
⇒ ΔOAK cân tại O
⇒ 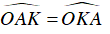
Xét tam giác BKC vuông tại K, có H là trung điểm của BC(do tam giác ABC cân tại A)
⇒ BH = HK = HC.
⇒ ΔHCK cân tại H
⇒ 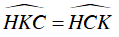
Ta lại có: 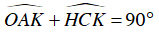
Từ (1), (2) và (3) suy ra: 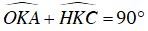
Từ đó suy ra rằng HK là tiếp tuyến của đường tròn đường kính AI.
Câu 3 : Cho đường tròn (O) đường kính AB, lấy điểm M sao cho A nằm giữa B và M. Kẻ đường thẳng MC tiếp xúc với đường tròn (O) tại C. Từ O hạ đường thẳng vuông góc với CB tại H và cắt tia MC tại N. Khẳng định nào sau đây không đúng?
a. BN là tiếp tuyến của đường tròn (O)
b. BC là tiếp tuyến của đường tròn (O)
c. OC là tiếp tuyến của đường tròn (O, ON)
d. AC là tiếp tuyến của đường tròn (C, BC)
Hướng dẫn giải
Đáp án A
+ BC là dây của đường tròn (O), nên B sai.
+ Ta có 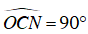
⇒ OC là dây của đường tròn đường kính ON, nên C sai.
+ Ta có AC là đường thẳng đi qua tâm của (C,BC) nên không thể là tiếp tuyến. Do đó D sai.
+ Ta có OH ⊥ BC
Xét tam giác OBC cân tại O (OB = OC) có OH là đường cao
⇒ OH là phân giác
Xét ΔOCN và ΔOBN , ta có :
OC = OB
ON : cạnh chung
⇒ ΔOCN = ΔOBN (c-g-c)
⇒ 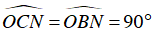
⇒ BN ⊥ OB
Vậy BN là tiếp tuyến của đường tròn (O).
Câu 4 : Cho tam giác ABC vuông tại A, đường cao AH. Đường tròn tâm O đường kính AH cắt AB tại E, đường tròn tâm O’ đường kính HC cắt AC tại F. Khi đó:
a. EF là tiếp tuyến của đường tròn (H, HO)
B, O’F là tiếp tuyến của đường tròn
c. EF là tiếp tuyến chung của hai đường tròn (O) và (O’).
d. OF là tiếp tuyến của đường tròn (C, CF).
Hướng dẫn giải
Đáp án
EF không vuông góc với OH nên EF không là tiếp tuyến của (H,HO).
EF là không là tiếp tuyến chung của hai đường tròn (O) và (O’).
EF không vuông góc với CF nên EF không là tiếp tuyến của (C,CF).
Xét tam giác O’CF cân tại O’(O’C = O’F)
⇒ 
Ta lại có: 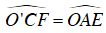
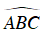
⇒
Mà 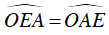
⇒
Mà 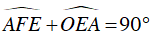
⇒
Vậy O’F là tiếp tuyến của đường tròn 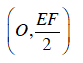
Câu 5 : Cho nửa đường tròn (O) đường kính AB. Trên nửa mặt phẳng bờ AB chứa nửa đường tròn dựng hai tiếp tuyến Ax và By. Trên tia Ax lấy điểm C, trên tia Ay lấy điểm D. Điều kiện cần và đủ để CD tiếp xúc với đường tròn (O) là:
A. AB2 = AC.BD
B. AB2 = 2AC.BD
C. AB2 = 4AC.BD
D. AB2 = AC2.BD2
Hướng dẫn giải
Đáp án C
( ⇒ ) CD tiếp xúc với đường tròn (O)
CD là tiếp tuyến của (O) tại H
CD cắt Ax tại C, theo tính chất hai tiếp tuyến cắt nhau, ta có:
AC = CH và OC là tia phân giác của 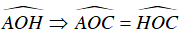
CD cắt By tại D, theo tính chất hai tiếp tuyến cắt nhau, ta có:
và OD là phân giác của 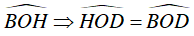
Từ (1) và (2) suy ra
Ta lại có:
Xét tam giác COD vuông tại O, OH ⊥ CD :
OH2 = DH.CH = DB.AC
⇔
(⇐)
Kẻ OH ⊥ CD
Trên tia đối của tia BD lấy điểm E sao cho BE = AC
Ta có:
Mà AC = BE ⇒ BE.BD = R2 = OB2
⇒ ΔDOE vuông tại O
Xét ΔOAB và ΔOBE , ta có:
AC = BE (gt)
OA = OB (=R)
⇒ ΔOAB = ΔOBE
⇒ 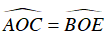
Ta có:
Nên C, O, E thẳng hàng
Xét tam giác DCE, có:
OD vừa là đường cao vừa là đường trung tuyến của ΔCDE nên OD cũng là đường phân giác.
⇒ 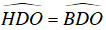
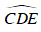
Xét ΔOHD và ΔOBD , có:
OD chung
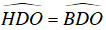
⇒ ΔOHD = ΔOBD (cạnh huyền - góc nhọn)
⇒ OH = OB ⇒ CD tiếp xúc với đường tròn (O).
Câu 6 : Cho đường tròn (O, R) đường kính AB. Vẽ dây cung AC sao cho góc CAB bằng 30o . Trên tia đối của tia BA lấy điểm M sao cho BM = R. Khi đó:
a. AM là tiếp tuyến của đường tròn (O).
b. BM là tiếp tuyến của đường tròn (O).
c. CM là tiếp tuyến của đường tròn (O).
d. AB là tiếp tuyến của đường tròn (O).
Hướng dẫn giải
Đáp án C
Ta có: 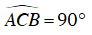
⇒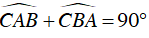
⇒
Xét tam giác OBC có OB = OC và
⇒ ΔOBC đều
⇒ OB = BC = BM
⇒
⇒ ΔOCM vuông tại C
⇒ 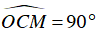
Vậy CM là tiếp tuyến của đường tròn (O).
Câu 7 : Trong các phát biểu dưới đây, phát biểu nào sau đây đúng:
A. Đường thẳng d được gọi là tiếp tuyến của (O) khi chúng có điểm chung
B. Đường thẳng d được gọi là tiếp tuyến của (O) khi d vuông góc với bán kính tại A
C. Đường thẳng d được gọi là tiếp tuyến của (O) khi d vuông góc với bán kính tại A và A thuộc (O)
D. Đường thẳng d được gọi là tiếp tuyến của (O) khi d vuông góc với bán kính tại A và OA > R.
Hướng dẫn giải
Đáp án C
Theo định nghĩa của tiếp tuyến, Đường thẳng d được gọi là tiếp tuyến của (O) khi d vuông góc với bán kính tại A và OA = R.
Câu 8 : Cho tam giác ABC vuông ở A. Vẽ đường cao AH, gọi D là điểm đối xứng với B qua H. Vẽ đường tròn đường kính CD cắt CA ở E, O là trung điểm của CD Khi đó, góc HEO bằng:
Hướng dẫn giải
Đáp án A
Gọi O là tâm đường tròn đường kính CD
E nằm trên đường tròn đg kính CD
⇒ ΔDE vuông tại E
⇒ 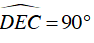
Mà AB AC (do tam giác ABC vuông tại A)
⇒ DE // AB ( từ vuông góc đến song song)
⇒ ABDE là hình thang
Gọi M là trung điểm của AE
Ta có: H là trung điểm của BD (D đối xứng với B qua H)
⇒ HM là đg trung bình của hình thang ABDE
⇒ HM // AB HM ⊥ AC
Xét ΔAHE có HM vừa là đường trung tuyến, vừa là đường cao
⇒ ΔAHE cân tại H ⇒ 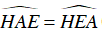
+ ΔCOE cân tại O ⇒ 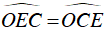
Mà 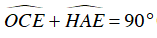
⇒
Mà
⇒ 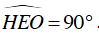
Câu 9 : Cho tam giác ABC vuông tại A, đường cao AH. Đường tròn tâm I đường kính BH cắt AB tại E, đường tròn tâm J đường kính HC cắt AC tại F. Khi đó:
A. EH là tiếp tuyến chung của hai đường tròn (I) và (J) tại H
B. BH là tiếp tuyến chung của hai đường tròn (I) và (J) tại H
C. AH là tiếp tuyến chung của hai đường tròn (I) và (J) tại H
D. CH là tiếp tuyến chung của hai đường tròn (I) và (J) tại H
Hướng dẫn giải
Đáp án C
Ta nhận thấy H ∈ (I), H ∈ (J)
Mà AH ⊥ JH , AH ⊥ IH
Suy ra AH là tiếp tuyến chung của hai đường tròn (I) và (J) tại H.
Câu 10 : Cho tam giác ABC có AB=3cm, AC=4cm và BC=5cm. Khi đó:
A. AB là tiếp tuyến của (C;3cm).
B. AC là tiếp tuyến của (B;3cm).
C. AB là tiếp tuyến của (B;4cm).
D. AC là tiếp tuyến của (C;4cm).
Hướng dẫn giải
Đáp án B
Vì AB = 3cm ⇒ A ∈ (B;3cm).
Xét tam giác ABC, có :
BC2 = 52 = 25
AB2 + AC2 = 32 + 42 = 9 + 16 = 25
⇒ AB2 + AC2 = BC2
Theo định lý Py – ta – go đảo suy ra tam giác ABC vuông tại A
⇒ AB ⊥ AC
⇒ AC là tiếp tuyến của (B;3cm).
2. Bài tập tự luận
Bài 1: Cho ΔABC nội tiếp đường tròn (O), (AB < AC). Trên tia đối của tia BC lấy điểm M sao cho MA2 = MB.MC. Chứng minh rằng: MA là tiếp tuyến của đường tròn (O).
Lời giải:
Vì MA2 = MB.MC ⇒
Xét ΔMAC và ΔMBA có
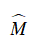
⇒ ΔMAC ∼ ΔMBA (c.g.c)
⇒ 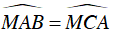
Kẻ đường kính AD của (O)
Ta có 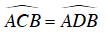
Mà 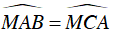
Suy ra 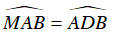
Lại có 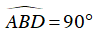
⇒ 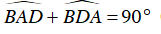
Từ (3) và (4) suy ra 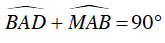
⇒ OA ⊥ MA
Do A ∈ (O)
⇒ MA là tiếp tuyến của (O).
Bài 2 : Cho đường tròn tâm O đường kính AB. C là một điểm thay đổi trên đường tròn (O). Tiếp tuyến tại C của (O) cắt AB tại D. Đường thẳng qua O và vuông góc với phân giác của 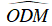
Lời giải:
Kẻ OH ⊥ d ⇒
Ta có CD là tiếp tuyến của (O) nên OC ⊥ CD tại C ⇒
Gọi E là giao điểm của tia phân giác 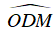
Xét tam giác MDO có : DE là phân giác 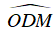
⇒ ΔDOM cân tại D
⇒ 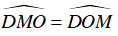
Ta lại có : d//AB ⇒ 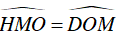
⇒
Xét ΔOHM và ΔOCM , có :
OM: cạnh chung
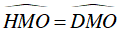
⇒ ΔOHM = Δ OCM (cạnh huyền – góc nhọn)
⇒ OH = OC = R (hai cạnh tương ứng)
⇒ H ∈ (O;R)
Do đó d là tiếp tuyến của (O;R).
Bài 3: Cho tam giác ABC nhọn. Vẽ đường tròn tâm O đường kính BC, cắt AB,AC lần lượt tại E và F. BF và CE cắt nhau tại I. Gọi M là trung điểm của AI. Chứng minh MF là tiếp tuyến của (O).
Lời giải:
Ta có : 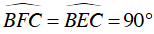
⇒ BF ⊥ AC , CE ⊥ AB
Xét tam giác ABC, có BF ∩ CE = {I}
⇒ I là trực tâm tam giác ABC
Gọi H là giao điểm của AI với BC
⇒ AH ⊥ BC tại H
Xét tam giác AFI vuông tại F, có M là trung điểm của AI
⇒ FM = MA = MI
⇒ ΔFMA cân tại M
⇒ 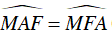
Xét tam giác OFC, có OF = OC
⇒ FOC cân tại O
⇒ 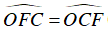
Xét tam giác AHC vuông tại H, có: 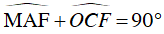
Từ (1), (2) và (3)
Mà
⇒
⇒ MF ⊥ OF
Vậy MF là tiếp tuyến của (O).
3. Bài tập tự luyện
Bài 1. Cho tam giác ABC cân tại A, nội tiếp đường tròn tâm O. Vẽ hình bình hành ABCD. Tiếp tuyến tại C của đường tròn cắt đường thẳng AD tại N. Chứng minh:
a) Đường thẳng AD là tiếp tuyến của (O);
b) Ba đường thẳng AC, BD, ON đồng quy.
Bài 2. Từ một điểm A ở bên ngoài đường tròn (O; R), vẽ hai tiếp tuyến AB, AC với (O). Đường thẳng vuông góc với OB tại O cắt tia AC tại N. Đường thẳng vuông góc với OC tại O cắt tia AB tại M.
a) Chứng minh tứ giác AMON là hình thoi;
b) Điểm A phải cách O một khoảng là bao nhiêu để MN là tiếp tuyến của (O).
Bài 3. Cho nửa đường tròn tâm O đường kính AB. Lấy M trên (O) và tiếp tuyến tại M cắt tiếp tuyến tại A và B của (O) ở C và D; AM cắt OC tại E, BM cắt OD tại F.
a) Chứng minh ;
b) Tứ giác MEOF là hình gì;
c) Chứng minh AB là tiếp tuyến của đường tròn đường kính CD.
Bài 4. Cho tam giác ABC vuông tại A, AH là đường cao. Gọi BD, CE là các tiếp tuyến của đường tròn (A; AH) với D , E là các tiếp điểm. Chứng minh:
a) Ba điểm D, A, E thẳng hàng;
b) DE tiếp xúc với đường tròn đường kính BC
Bài 5. Cho điểm M nằm trên nửa đường tròn tâm O đường kính AB. Vẽ tiếp tuyến xy. Kẻ AD , BC cùng vuông góc với xy (các điểm D, C nằm trên xy). Xác định vị trí của điểm M trên nửa đường tròn ( ) O sao cho diện tích tứ giác ABCD đạt giá trị lớn nhất.
Bài 6. Cho tam giác IMN có cạnh IM và cạnh IN bằng nhau. Kẻ đường cao IH và MK giao nhau tại A. Hãy chứng minh:
a. Đường tròn đường kính IA đi qua điểm K
b. Đường tròn đường kính IA có tiếp tuyến là HK
Bài 7. Cho đường tròn tâm I, AB là đường kính. Cho hai tia Ax và By là hai tiếp tuyến của đường tròn. Lấy hai điểm C, D với C nằm trên tia Ax, D nằm trên tia By sao cho góc CID bằng 90 độ. Hãy chứng minh rằng CD là tiếp tuyến của đường tròn tâm I.
Bài 8. Cho đường tròn tâm O bán kính R, đường kính MN. Vẽ đoạn MA sao cho bằng 30 độ. Trên tia đối của tia NM lấy điểm I sao cho NI bằng bán kính R. Chứng minh:
a. IA là một tiếp tuyến của đường tròn tâm O
b. IA = R
Bài 9. Cho đường tròn tâm O trên đường tròn lấy hai điểm A, B. Kể hai tiếp tuyến từ B và C giao nhau tại A.
a. Chứng minh đoạn AO là đường trung trực của đoạn BC,
b. Vẽ đường kính CD của đường tròn (O). Chứng minh đoạn BD và đoạn OA song song với nhau.
Bài 10. Cho hai đường tròn tâm O, điểm M nằm ngoài đường tròn. Từ M vẽ hai tiếp tuyến ME và MF tiếp điểm E và F sao cho EMO = 60 độ. Biết số đo chu vi tam giác MEF = 60 cm.
a. Tính độ dài đoạn EF
b. Tính số đó diện tích tam giác MEF
Bài 12. Cho hai tiếp tuyến tại điểm A và điểm B của đường tròn tâm O giao nhau tại điểm M. Đường thẳng vuông góc với đoạn OA tại điểm O cắt đoạn MB tại điểm C. Chứng minh đoạn CM bằng đoạn CO.
Bài 13. Cho đường tròn tâm I bán kính R, lấy A là một điểm nằm ngoài đường tròn. Vẽ các tiếp tuyến đường tròn AB và AC (trong đó B và C là hai tiếp điểm) Chứng minh = 30 độ khi và chỉ khi đoạn OA bằng độ dài đường kính.
Bài 14. Cho nửa đường tròn tâm O có MN là đường kính. Vẽ hai tiếp tuyến Mx và Ny. ĐIểm I nằm trên đường trong sao cho tiếp tuyến tại I cắt Mx tại C, cắt Ny tại D. Chứng minh:
a. MC + MD = CD
b. = 90 độ
c. MC x ND = OM2
Bài 15. Cho đường tròn O đường kính MN. Mx và Ny là hai tia của tiếp tuyến của đường tròn O trong đó có Mx và Ny cùng nửa mặt phẳng bở là đường thằng MN. Trên tia Mx lấy điểm C, trên Ny lấy điểm D sao cho bằng 90 độ. Chứng minh rằng CD là tiếp tuyến của đường tròn tâm O.