Tailieumoi.vn xin giới thiệu bộ đề thi học kì 1 môn Toán lớp 9 sách Cánh diều năm 2024 - 2025. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THCS dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi Học kì 1 Toán 9. Mời các bạn cùng đón xem:
Đề thi học kì 1 Toán 9 Cánh diều có đáp án năm 2025
Đề thi học kì 1 Toán 9 Cánh diều có đáp án - Đề 1
Phòng Giáo dục và Đào tạo ...
Đề thi Học kì 1 - Cánh diều
Năm học 2024 - 2025
Môn: Toán lớp 9
Thời gian làm bài: phút
(Đề số 1)
Câu 1 : Phương trình có nghiệm tổng quát là:
.
.
.
.
Câu 2 : Nghiệm của phương trình là
.
.
.
.
Câu 3 : Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
.
.
.
.
Câu 4 : Căn bậc hai số học của 25 là
5.
-5.
5 và -5.
625 và - 625.
Câu 5 : Biểu thức xác định khi
.
.
.
.
Câu 6 : Rút gọn biểu thức ta được
.
.
.
.
Câu 7 : Kết quả của là
.
.
.
.
Câu 8 : Cho tam giác ABC có AB = 9cm, AC = 12cm, BC = 15cm. Độ dài đường cao AH (H BC) của tam giác ABC là
8,4cm.
7,2cm.
6,8cm.
4,2cm.
Câu 9 : Đường tròn là hình
không có trục đối xứng.
có một trục đối xứng.
có hai trục đối xứng.
có vô số trục đối xứng.
Câu 10 : Hình nào dưới đây biểu diễn góc ở tâm?
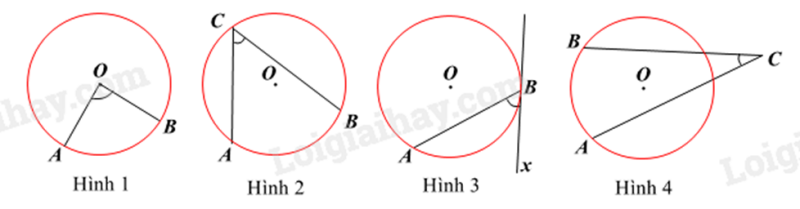
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Câu 11 : Cho đường tròn (O) đường kính 8cm và đường tròn . OA là một bán kính của (O) (A (O)) và là trung điểm của đoạn . Vị trí tương đối của hai đường tròn trên là
Tiếp xúc ngoài.
Cắt nhau.
Ở ngoài nhau.
Tiếp xúc trong.
Câu 12 : Hai đường tròn và tiếp xúc ngoài. Số tiếp tuyến chung của chúng là
1.
2.
3.
4.
Câu 1 : Cho với
a) Rút gọn A.
b) Tìm để .
c) Tìm x để A đạt GTNN.
Câu 2 : Ngày chủ nhật hai bạn Tâm và Hiếu được bố mẹ chở đi siêu thị để mua sắm. Khi đến quầy thức ăn Tâm mua chiếc bánh và ly nước, Hiếu mua chiếc bánh và ly nước. Tổng số tiền ăn uống của cả hai bạn là 252 nghìn đồng. Biết giá tiền của một ly nước cao hơn giá tiền của một chiếc bánh là nghìn đồng. Hỏi giá tiền của một cái bánh và một ly nước là bao nhiêu?
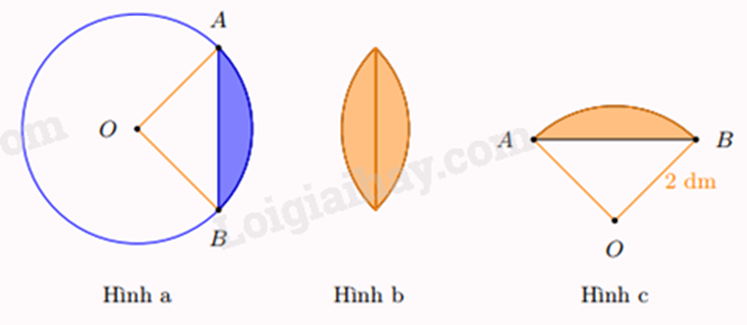
Câu 3 : Hình viên phân là hình giới hạn bởi một cung tròn và dây cung (tương ứng) của đường tròn (minh họa bởi phần tô đậm ở hình a). Người ta làm một họa tiết trang trí bằng cách ghép hai hình viên phân bằng nhau (hình b), mỗi hình viên phân đó có góc ở tâm tương ứng là và bán kính đường tròn tương ứng là (hình c). Tính diện tích của họa tiết trang trí đó (lấy )
Câu 4 : Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ các đường kính AOB, AO’C. Gọi DE là tiếp tuyến chung của hai đường tròn, và . Gọi M là giao điểm của BD và CE.
a) Tính số đo của .
b) Tứ giác ADME là hình gì?
c) Chứng minh MA là tiếp tuyến chung của hai đường tròn.
Câu 5 : Một bánh xe có dạng hình tròn bán kính 20cm lăn đến bức tường hợp với mặt đất một góc . Hãy tính khoảng cách ngắn nhất từ tâm bánh xe đến góc tường.

ĐÁP ÁN
| 1B | 2A | 3C | 4A | 5B | 6C |
| 7D | 8B | 9D | 10A | 11D | 12C |
Câu 1 :
a) Với ta có:
.
b) Ta có
Đặt , để A nguyên khi x nguyên thì B là ước nguyên của 2.
Vì nên , suy ra B là ước nguyên dương của 2.
Ư
TH1: suy ra
TH2: suy ra
Vậy thì A nguyên.
c) Ta có .
Vì nên
Suy ra
Do đó hay .
Dấu “=” xảy ra khi
Vậy khi .
Câu 2 :
Gọi giá tiền một chiếc bánh và một ly nước lần lượt là nghìn đồng ()
Vì Tâm mua chiếc bánh và ly nước, Hiếu mua chiếc bánh và ly nước nên tổng số bánh và nước hai bạn mua là 11 chiếc bánh và 6 ly nước. Tổng số tiền ăn uống của hai bạn là 252 nghìn đồng nên ta có phương trình: .
Vì giá tiền của một ly nước cao hơn giá tiền của một chiếc bánh là nghìn đồng nên hay .
Ta có hệ phương trình
Vậy giá một chiếc bánh là nghìn đồng, giá một ly nước là nghìn đồng.
Câu 3 :
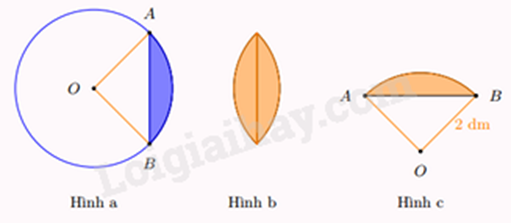
Vì góc ở tâm bằng nên tam giác OAB vuông tại O.
+ Diện tích tam giác là:
+ Do sđ nên diện tích hình quạt tròn tương ứng là:
Suy ra diện tích hình viên phân là:
Diện tích của họa tiết trang trí đó là:
.
Vậy diện tích của họa tiết trang trí đó khoảng .
Câu 4 :
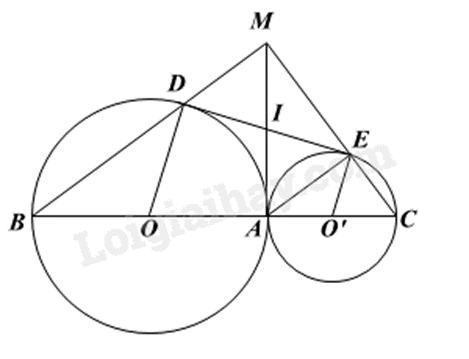
Từ A kẻ tiếp tuyến chung của hai đường tròn, tiếp tuyến này cắt DE tại I.
Theo tính chất hai tiếp tuyến cắt nhau, ta có ID = IA = IE nên vuông tại A. Suy ra .
b) Vì AB và AC là các đường kính của (O) và (O’) nên .
Suy ra .
Mà nên tứ giác ADME là hình chữ nhật.
c) Vì tứ giác ADME là hình chữ nhật nên 3 điểm M, I, A thẳng hàng.
Do vậy MA là tiếp tuyến chung của hai đường trong (O); (O’).
Câu 5 :
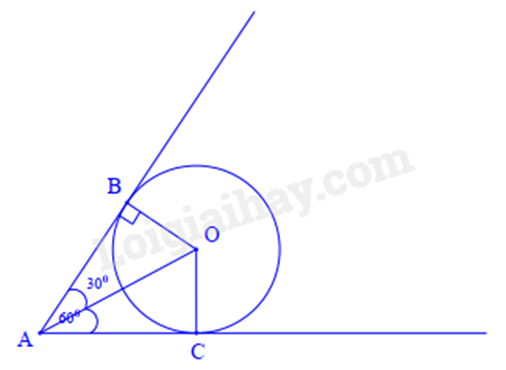
Ta có: OA = OC = 20cm.
Khi bánh xe chạm tới bức tường thì không thể di chuyển vào thêm được nữa. Điều này có nghĩa khoảng cách của tâm bánh xe đến góc tường ngắn nhất là khi bánh xe tiếp xúc với bức tường và mặt đất.
Gọi AB và AC là hai đoạn biểu diễn mặt tường và mặt đất tiếp xúc với đường tròn (O), khi đó AB và AC là hai tiếp tuyến cắt nhau tại A của đường tròn (O).
Vì nên (tính chất hai tiếp tuyến cắt nhau).
Xét tam giác ABO vuông tại B (vì AB là tiếp tuyến của (O) nên ), ta có:
(tỉ số lượng giác trong tam giác vuông)
Suy ra
Vậy khoảng cách ngắn nhất từ bánh xe đến góc tường là 40cm.
Đề thi học kì 1 Toán 9 Cánh diều có đáp án - Đề 2
Phòng Giáo dục và Đào tạo ...
Đề thi Học kì 1 - Cánh diều
Năm học 2024 - 2025
Môn: Toán lớp 9
Thời gian làm bài: phút
(Đề số 2)
A. TRẮC NGHIỆM (3,0 điểm)
Câu 1. Điều kiện xác định của phương trình là
A. x ≠ 7 và x ≠ –4.
B. x ≠ 4.
C. x ≠ –7 và x ≠ 4.
D. x ≠ –7.
Câu 2. Trong các hệ phương trình dưới đây, hệ phương trình nào là hệ phương trình bậc nhất hai ẩn?
A. .
B. .
C. .
D. .
Câu 3. Tất cả các nghiệm của phương trình 4x + 2y – 6 = 0 được biểu diễn bởi đường thẳng nào sau đây?
A. y = 2x – 3.
B. y = –2x + 3.
C. y = 3x + 2.
D. y = 4x – 6.
Câu 4. Bất đẳng thức n ≤ 3 có thể được phát biểu là
A. n lớn hơn 3.
B. n nhỏ hơn 3.
C. n không lớn hơn 3.
D. n không nhỏ hơn 3.
Câu 5. Nghiệm của bất phương trình 5x – 4 – 3(2x – 9) ≤ 5x – 8 là
A. .
B. .
C. .
D. .
Câu 6. Với mọi số a, ta luôn có:
A. .
B. .
C. .
D. .
Câu 7. Với hai số a < 0, b > 0, biểu thức có giá trị là
A. –a2.
B. a2.
C. a2b2.
D. –a2b2.
Câu 8. Cho β là góc nhọn bất kì. Khẳng định nào sau đây đúng?
A. .
B. .
C. .
D. .
Câu 9. Cho tam giác ABC vuông tại C có AC = 1,2 cm, AB = 1,5 cm. Tỉ số lượng giác tanB là
A. .
B. .
C. .
D. .
Câu 10. Cho hai đường tròn (O; R) và (O’; r) với R > r cắt nhau tại hai điểm phân biệt và OO’ = d. Chọn khẳng định đúng?
A. d > R + r.
B. d = R – r.
C. d < R – r.
D. R – r < d < R + r.
Câu 11. Khẳng định nào sau đây là sai?
A. Trong một đường tròn, góc nội tiếp chắn nửa đường tròn là góc vuông.
B. Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo góc ở tâm cùng chắn một cung.
C. Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau.
D. Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung.
Câu 12. Một công viên có hồ nước hình tròn với bán kính 50 m. Xung quanh hồ, người ta xây một lối đi hình vành khăn có chiều rộng 5 m (hình vẽ). Diện tích lối đi của công viên là
A. 252π m2.
B. 25π m2.
C. 5π m2.
D. 525π m2.
B. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm) Cho hai biểu thức và với x > 0, x ≠ 1.
a) Tính giá trị của biểu thức A khi x = 16.
b) Rút gọn biểu thức B.
c) Xét biểu thức P = AB. Tìm tất cả các giá trị của x sao cho P nhận giá trị nguyên.
Bài 2. (2,0 điểm)
1. Giải các phương trình và bất phương trình sau:
a) .
b) .
2. Giải bài toán sau bằng cách lập hệ phương trình:
Có hai loại quặng chứa 75% sắt và 50% sắt. Tính khối lượng của mỗi loại quặng đem trộn để được 25 tấn quặng chứa 66% sắt.
Bài 3. (1,0 điểm) Trên nóc của một tòa nhà có một cột ăng – ten cao 5 m. Từ vị trí quan sát A cao 7 m so với mặt đất, có thể nhìn thấy đỉnh B và đỉnh C của một cột ăng – ten dưới góc 50° và 40° so với phương nằm ngang. Tính chiều cao của tòa nhà.
Bài 4. (2,0 điểm) Cho đường tròn (O) và một điểm A nằm ngoài đường tròn. Các tiếp tuyến với đường tròn kẻ từ A tiếp xúc với đường tròn tại B và C. Gọi H là giao điểm của OA và BC, kẻ đường kính BD của đường tròn (O), hạ CM ⊥ BD tại M. Tia AO cắt đường tròn (O) tại E, F.
a) Chứng minh rằng ∆CMD ᔕ ∆ACO.
b) Chứng minh rằng BE là phân giác của .
c) Cho và AH = 4 cm. Tính diện tích hình quạt giới hạn bởi các bán kính OB, OC và cung nhỏ BC.
Bài 5. (0,5 điểm) Một tấm bìa cứng hình chữ nhật có chiều dài là 50 cm và chiều rộng là 30 cm. Bạn Linh cắt ở mỗi góc một tấm bìa hình vuông cạnh x (cm) và xếp phần còn lại thành một hình hộp không nắp. Tìm x để diện tích xung quanh của hình hộp chữ nhật sau khi cắt là lớn nhất.
-----HẾT-----
ĐÁP ÁN & HƯỚNG DẪN
A. TRẮC NGHIỆM (3,0 điểm)
Bảng đáp án trắc nghiệm:
|
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Đáp án |
B |
A |
B |
C |
A |
B |
B |
C |
B |
D |
D |
D |
B. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm)
Hướng dẫn giải
a) Thay x = 16 (thỏa mãn điều kiện) vào biểu thức A, ta được:
A = .
Vậy khi x = 16.
2) Với x > 0, x ≠ 1, ta có:
Vậy với x > 0, x ≠ 1 thì B = .
2) – Với x > 0, x ≠ 1, ta có:
P = A.B = = =
Với x > 0, x ≠ 1, ta cũng có:
⦁ nên , do đó suy ra
⦁ nên , do đó suy ra
Khi đó, –2 < P < 1.
– Để P nhận giá trị nguyên thì P = –1 hoặc P = 0.
⦁ Với P = –1, ta có , suy ra , nên , do đó , hay (thỏa mãn).
⦁ Với P = 0, ta có , suy ra , nên , do đó , hay x = 4 (thỏa mãn).
Vậy .
Bài 2. (2,0 điểm)
Hướng dẫn giải
1. Giải các phương trình, bất phương trình sau:
2. Gọi x, y (tấn) lần lượt là khối lượng quặng chứa 75% sắt và 50% sắt (x, y > 0).
Theo đề, tổng khối lượng quặng là 25 tấn nên ta có: x + y = 25. (1)
Khối lượng sắt trong 25 tấn quặng chứa 66% sắt là: 25.66% = 16,5 (tấn).
Khối lượng sắt trong x (tấn) quặng chứa 75% sắt là: x.75% = 0,75x (tấn).
Khối lượng sắt trong y (tấn) quặng chứa 50% sắt là: y.50% = 0,5y (tấn).
Do đó, ta có phương trình: 0,75x + 0,5y = 16,5. (2)
Từ (1) và (2) ta có hệ phương trình: .
Từ phương trình (1), suy ra y = 25 – x.
Thay y = 25 – x vào phương trình (2) ta được:
0,75x + 0,5(25 – x) = 16,5
0,75x + 12,5 – 0,5x = 16,5
0,25x = 4
x = 16 (thỏa mãn).
Thay x = 16 vào phương trình y = 25 – x, ta được y = 9 (thỏa mãn).
Vậy cần trộn 16 tấn quặng chứa 75% sắt và 9 tấn quặng chứa 50% sắt để được 25 tấn quặng chứa 66% sắt.
Bài 3. (1,0 điểm)
Hướng dẫn giải
Chiều cao của tòa nhà chính là độ dài đoạn thẳng BH.
Xét tam giác CAE vuông tại E, ta có:
CE = AE. = AE.tan 40° (m) (1).
Xét tam giác BAE vuông ở E, ta có:
BE = AE. = AE.tan 50° (m) (2).
Từ (1) và (2) suy ra BC = BE - CE = AE tan 50° - AE tan 40°
BC = AE (tan 50° - tan 40°)
5 = AE (tan 50° - tan 40°)
AE = (m)
Suy ra CE = = ≈ 11,9 (m).
Chiều cao của tòa nhà là: 5 + 11,9 + 7 ≈ 23,9 (m).
Vậy tòa nhà cao khoảng 23,9 mét.
Bài 4. (2,0 điểm)
Hướng dẫn giải
a) Ta có: AB, AC là hai tiếp tuyến của đường tròn (O), suy ra OA là đường phân giác của (tính chất) nên .
Xét đường tròn (O), ta có: (góc nội tiếp và góc ở tâm cùng chắn cung BC)
Do đó, .
Xét ∆CMD và ∆ACO có:
và (do )
Do đó ∆CMD ᔕ ∆ACO (g.g).
b) Xét đường tròn (O), ta có: (góc nội tiếp chắn nửa đường tròn).
Ta có nên
Suy ra .
Lại có: (vì ∆BOF cân tại O do OB = OF), suy ra (1)
Mà (hai góc nội tiếp cùng chắn cung EC của đường tròn tâm O) (2)
Từ (1) và (2) suy ra . (3)
Mặt khác, AB = AC (tính chất hai tiếp tuyến cắt nhau) và OB = OC
Suy ra OA là đường trung trực của BC mà E ∈ OA, suy ra EB = EC.
Do đó ∆EBC cân tại E nên . (4)
Từ (3) và (4) suy ra nên BE là tia phân giác của góc B trong tam giác ABH.
Vậy BE là phân giác của .
c) Theo câu a, ∆ACO ᔕ ∆CMD (g.g), suy ra .
Suy ra .
Do đó, hay .
Xét ∆AHC vuông tại H, có:
Suy ra AC = (cm).
Xét ∆ACO vuông tại C, có: OC = (cm).
Diện tích hình quạt giới hạn bởi các bán kính OB, OC và cung nhỏ BC là:
S = (cm2).
Bài 5. (0,5 điểm)
Hướng dẫn giải
Diện tích tấm bìa hình chữ nhật này là: 50 . 30 = 1 500 (cm2).
Chiều dài sau khi cắt tấm bìa là: 50 – 2x (cm).
Chiều rộng sau khi cắt tấm bìa là: 30 – 2x (cm).
Diện tích xung quanh của hộp là:
2x(50 – 2x + 30 – 2x) = 2x(80 – 4x) = –8x2 +160x (cm2).
Để diện tích xung quanh của hình hộp chữ nhật sau khi cắt là lớn nhất thì –8x2 +160x đạt giá trị lớn nhất.
Ta có: –8x2 +160x = –8(x2 – 20x + 100) + 800 = –8(x – 10)2 + 800.
Với mọi x > 0 ta có: –8(x – 10)2 ≤ 0 nên –8(x – 10)2 + 800 ≤ 800.
Dấu “=” xảy ra khi x – 10 = 0 hay x = 10.
Vậy diện tích xung quanh hình hộp chữ nhật là 800 cm2 khi x = 10 cm.
-----HẾT-----