Bộ 10 đề thi giữa kì 1 Toán 9 Cánh diều có đáp án năm 2024

Thuy Quynh Ngày: 11-01-2025 Lớp 9

893

Tailieumoi.vn xin giới thiệu bộ đề thi giữa kì 1 môn Toán lớp 9 sách Cánh diều năm 2024 - 2025. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THCS dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi Giữa học kì 1 Toán 9. Mời các bạn cùng đón xem:

Đề thi giữa kì 1 Toán 9 Cánh diều có đáp án năm 2024

Đề thi giữa kì 1 Toán 9 Cánh diều có đáp án - Đề 1

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Cánh diều

Năm học 2024 - 2025

Môn: Toán lớp 9

Thời gian làm bài: phút

(Đề số 1)

I. Trắc nghiệm

Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1 : Nghiệm của phương trình $x + 2 y = 5$ là

A.

$(x; y) = (1; - 2)$ .
B.

$(x; y) = (1; 2)$ .
C.

$(x; y) = (2; - 1)$ .
D.

$(x; y) = (2; 1)$ .

Câu 2 : Cặp số nào sau đây là nghiệm của hệ phương trình ${\begin{cases} x + 2 y = 3 \\ y = 1 \end{cases}$ ?

A.

$(x; y) = (1; 2)$ .
B.

$(x; y) = (2; 1)$ .
C.

$(x; y) = (1; - 1)$ .
D.

$(x; y) = (1; 1)$ .

Câu 3 : Nghiệm của phương trình $x (x + 1) = 0$ là

A.

$x = 0$ và $x = - 1$ .
B.

$x = 1$ .
C.

$x = 0$ .
D.

$x = 1$ và $x = - 1$ .

Câu 4 : Điều kiện xác định của phương trình $\frac{x + 3}{x - 1} + \frac{x - 2}{x} = 2$ là

A.

$x \neq 0; x \neq 1$ .
B.

$x = 0; x = 1$ .
C.

$x \neq 0$ .
D.

$x \neq 1$ .

Câu 5 : Cho $a > b$ , kết quả nào sau đây đúng?

A.

$a + 3 > b + 5$ .
B.

$a - 2 > b - 2$ .
C.

$- 2 a > - 2 b$ .
D.

$2 a > 3 b$ .

Câu 6 : Cho $- 2 a \leq - 2 b$ , kết quả nào sau đây là đúng?

A.

$a \leq b$ .
B.

$a - 2 \geq b - 1$ .
C.

$a > b$ .
D.

$2 a \geq 2 b$ .

Câu 7 : Trong các bất phương trình sau, bất phương trình nào không phải bất phương trình bậc nhất một ẩn?

A.

$5 x + 3 > 0$ .
B.

$- 2 x + 7 < 0$ .
C.

$3 x \leq 0$ .
D.

$2 x^{2} - 5 \geq 0$ .

Câu 8 : Trong các số sau, số nào là nghiệm của bất phương trình $2 - 3 x > 0$ ?

A.

$- 2$ .
B.

$2$ .
C.

$\frac{3}{2}$ .
D.

$\frac{2}{3}$ .

Câu 9 : Tỉ số lượng giác nào sau đây bằng $\sin 40^{\circ}$ ?

A.

$\sin 50^{\circ}$ .
B.

$\cos 50^{\circ}$ .
C.

$\tan 50^{\circ}$ .
D.

$\cot 50^{\circ}$ .

Câu 10 : Cho tam giác ABC có AB = 5, AC = 12, BC = 13. Khi đó tỉ số lượng giác cosB là

A.

$\frac{13}{5}$ .
B.

$\frac{5}{13}$ .
C.

$\frac{12}{5}$ .
D.

$\frac{5}{12}$ .

Câu 11 : Giá trị của biểu thức $\sin^{2} 25^{\circ} + \cos^{2} 25^{\circ}$ là

A.

0.
B.

1.
C.

2.
D.

3.

Câu 12 : Cho tam giác ABC vuông tại A có BC = 10cm, $\hat{C} = 30^{\circ}$ . Độ dài cạnh AB là:

A.

5,5cm.
B.

5cm.
C.

$5 \sqrt{3}$ cm.
D.

$5 \sqrt{2}$ cm.

II. Tự luận

Câu 1 : 1. Giải các phương trình và bất phương trình sau:

a) $x^{2} + 2 x - 3 = 0$

b) $\frac{2 x + 1}{2 x} - \frac{x}{x + 2} = 0$

c) $3 x - 5 < 2 x + 2$

d) $\frac{2 x + 3}{2} \geq \frac{1 - x}{3} + 1$

2. Giải hệ phương trình ${\begin{cases} 2 x - y = 4 \\ x + 2 y = - 3 \end{cases}$

Câu 2 : Để may khẩu trang tặng các gia đình khó khăn trong đại dịch COVID, khu phố của cô Mai và khu phố của cô Lan, lần thứ nhất đã may được 720 cái khẩu trang. Lần thứ hai do có nhiều bạn trẻ ở hai khu phố cùng tham gia may khẩu trang nên khu phố của cô Mai đã may vượt mức 15%, khu phố của cô Lan đã may vượt mức 12% so với lần thứ nhất. Tính số khẩu trang của mỗi khu phố may được trong lần thứ hai, biết rằng trong lần 2 cả hai khu phố đã may được 819 cái khẩu trang?

Câu 3 : Vào Tết Hàn thực, bác An dành không quá 1 giờ 30 phút để nặn bánh trôi và bánh chay. Bánh trôi cần 1 phút để nặn xong 1 chiếc, bánh chay cần 2 phút để nặn xong 1 chiếc. Tính số bánh trôi mà bác An có thể nặn nhiều nhất, biết bác An đã nặn được 15 chiếc bánh chay.

Bộ 10 đề thi giữa kì 1 Toán 9 Cánh diều có đáp án năm 2024 (ảnh 1)

Câu 4 : Cho tam giác ABC vuông tại A, đường cao AH.

a) Giải tam giác vuông biết $A B = 12 c m$ , $\hat{C} = 30^{\circ}$ .

b) Đường thẳng vuông góc với BC tại B cắt tia CA tại K. Kẻ AE vuông góc với BK $(E \in B K)$ . Chứng minh $E H^{2} = A K . A C$ .

c) Gọi M là trung điểm của cạnh AC. Kẻ MN vuông góc với BC tại N. Chứng minh $A N = B M . \cos C$ .

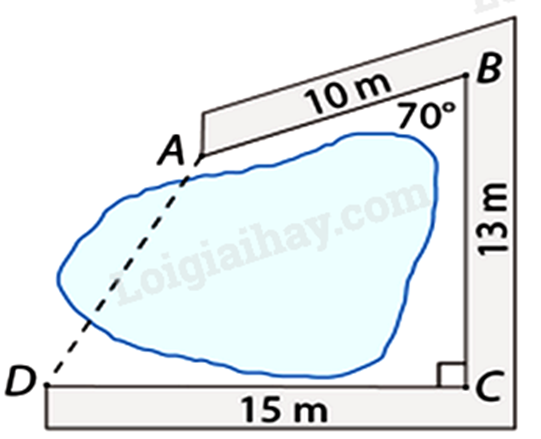
Câu 5 : Người ta làm một con đường gồm ba đoạn thẳng AB, BC, CD bao quanh hồ nước như hình sau. Tính khoảng cách AD. (làm tròn kết quả đến hàng phần trăm).

Bộ 10 đề thi giữa kì 1 Toán 9 Cánh diều có đáp án năm 2024 (ảnh 2)

ĐÁP ÁN

I. Trắc nghiệm

1. B	2. D	3. A	4. A	5. B	6. D
7. D	8. A	9. B	10. B	11. B	12. B

II. Tự luận

Câu 1:

1. Giải các phương trình và bất phương trình sau:

a) $x^{2} + 2 x - 3 = 0$

$\begin{array}{l} x^{2} - x + 3 x - 3 = 0 \\ (x^{2} - x) + (3 x - 3) = 0 \\ x (x - 1) + 3 (x - 1) = 0 \\ (x + 3) (x - 1) = 0 \end{array}$

+) $x + 3 = 0$ suy ra $x = - 3$ .

+) $x - 1 = 0$ suy ra $x = 1$ .

Vậy phương trình có hai nghiệm $x = - 3; x = 1$ .

b) $\frac{2 x + 1}{2 x} - \frac{x}{x + 2} = 0$

ĐKXĐ: $2 x \neq 0$ và $x + 2 \neq 0$

hay $x \neq 0$ và $x \neq - 2$ .

Ta có: $\frac{2 x + 1}{2 x} - \frac{x}{x + 2} = 0$

$\begin{array}{l} \frac{(2 x + 1) (x + 2)}{2 x (x + 2)} - \frac{x .2 x}{2 x (x + 2)} = 0 \\ (2 x + 1) (x + 2) - x .2 x = 0 \\ 2 x^{2} + x + 4 x + 2 - 2 x^{2} = 0 \\ 5 x + 2 = 0 \\ x = \frac{- 2}{5} (T M) \end{array}$

Vậy nghiệm của phương trình là $x = \frac{- 2}{5}$ .

c) $3 x - 5 < 2 x + 2$

$\begin{array}{l} 3 x - 2 x < 2 + 5 \\ x < 7 \end{array}$

Vậy nghiệm của bất phương trình là $x < 7$ .

d) $\frac{2 x + 3}{2} \geq \frac{1 - x}{3} + 1$

$\begin{array}{l} \frac{3 (2 x + 3)}{2.3} \geq \frac{2 (1 - x)}{3.2} + \frac{6}{6} \\ 3 (2 x + 3) \geq 2 (1 - x) + 6 \\ 6 x + 9 \geq 2 - 2 x + 6 \\ 6 x + 2 x \geq 2 + 6 - 9 \\ 8 x \geq - 1 \\ x \geq \frac{- 1}{8} \end{array}$

Vậy nghiệm của bất phương trình là $x \geq \frac{- 1}{8}$ .

2. Giải hệ phương trình ${\begin{cases} 2 x - y = 4 \\ x + 2 y = - 3 \end{cases}$

Ta có: ${\begin{cases} 2 x - y = 4 \\ x + 2 y = - 3 \end{cases}$

Nhân cả hai vế của phương trình $2 x - y = 4$ với 2, ta được hệ phương trình ${\begin{cases} 4 x - 2 y = 8 \\ x + 2 y = - 3 \end{cases}$ .

Cộng hai vế của hai phương trình trong hệ mới, ta được $5 x = 5$ suy ra $x = 1$ .

Thế vào phương trình $2 x - y = 4$ , ta được $2.1 - y = 4$ suy ra $y = - 2$ .

Vậy nghiệm của hệ phương trình là $(x; y) = (1; - 2)$ .

Câu 2:

Gọi số khẩu trang khu phố cô Mai may được là $x$ (khẩu trang, $x \in N^{*}, x < 720$ )

Số khẩu trang khu phố cô Lan may được là $y$ (khẩu trang, $y \in N^{*}, y < 720$ )

Vì tổng số khẩu trang của hai khu phố là 720 chiếc:

$x + y = 720$ (1)

Lần thứ hai khu phố cô Mai may được vượt mức 15%, nên số khẩu trang khu phố cô Mai may được là:

$x + 0, 15 x = 1, 15 x$ (khẩu trang)

Lần thứ hai khu phố cô Lan may được vượt mức 12%, nên số khẩu trang khu phố cô Lan may được là:

$y + 0, 12 y = 1, 12 y$ (khẩu trang)

Vì trong hai lần cả hai khu phố đã may được 819 cái khẩu trang:

$1, 15 x + 1, 12 y = 819$ (2)

Từ (1) và (2) ta có hệ phương trình:

${\begin{array}{l} x + y = 720 \\ 1, 15 x + 1, 12 y = 819 \end{array}$

Từ phương trình (1) ta có: $x = 720 - y$

Thay $x = 720 - y$ vào phương trình thứ hai:

$1, 15 (720 - y) + 1, 12 y = 819$

$1, 15.720 - 1, 15 y + 1, 12 y = 819$

$828 - 1, 15 y + 1, 12 y = 819$

$- 0, 03 y = - 9$

$y = 300$

Thay $y = 300$ vào phương trình $x + y = 720$ , ta được:

$x + 300 = 720$

$x = 420$

Vậy khu phố cô Mai may được 420 chiếc khẩu trang

Khu phố cô Lan may được 300 chiếc khẩu trang.

Câu 3:

Gọi số bánh trôi bác An có thể nặn là $x$ (chiếc), $x \in N^{*}$ .

Đổi 1 giờ 30 phút = 90 phút.

Vì bánh trôi cần 1 phút để nặn xong 1 chiếc, bánh chay cần 2 phút để nặn xong 1 chiếc, mà trong 1 giờ 30 phút bác An nặn được 15 chiếc bánh chay nên ta có bất phương trình:

$\begin{array}{l} 1. x + 2.15 \leq 90 \\ x + 30 \leq 90 \\ x \leq 60 \end{array}$

Vậy bác An có thể nặn nhiều nhất 60 chiếc bánh trôi.

Câu 4:

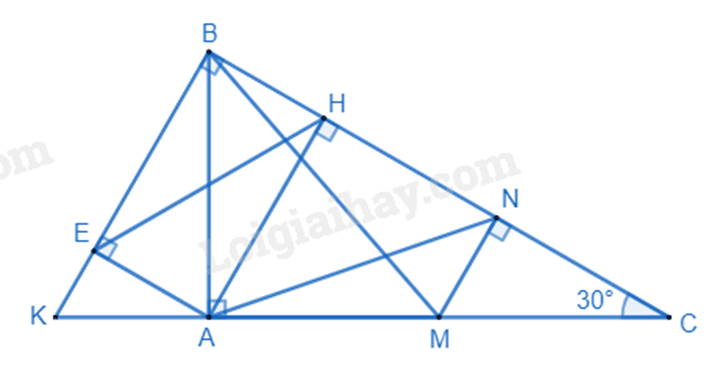
Bộ 10 đề thi giữa kì 1 Toán 9 Cánh diều có đáp án năm 2024 (ảnh 3)

a) Xét tam giác ABC vuông tại A, số đo góc B là:

$\hat{B} = 90^{\circ} - \hat{C} = 90^{\circ} - 30^{\circ} = 60^{\circ}$ .

Áp dụng tỉ số lượng giác trong tam giác vuông vào tam giác ABC, ta có: $\tan B = \frac{A C}{A B}$

suy ra $A C = A B . \tan B = 12. \tan 60^{\circ} = 12 \sqrt{3} (c m)$

Áp dụng định lí Pythagore vào tam giác vuông, ta có:

$B C = \sqrt{A B^{2} + A C^{2}} = \sqrt{12^{2} + {(12 \sqrt{3})}^{2}} = 24 (c m)$

Vậy $\hat{B} = 60^{\circ}, A C = 12 \sqrt{3} c m, B C = 24 c m$ .

b) Xét tứ giác AHBE có: $\hat{H} = \hat{B} = \hat{E} (= 90^{\circ})$ nên tứ giác AHBE là hình chữ nhật, suy ra AB = HE. (1)

Xét tam giác ABK và tam giác ACB có:

$\hat{B A K} = \hat{C A B} (= 90^{\circ})$

$\hat{A K B} = \hat{A B C}$ (cùng phụ với $\hat{C}$ )

suy ra $Δ A B K ∽ Δ B C K (g . g)$

Do đó $\frac{A B}{A K} = \frac{A C}{A B}$ nên $A B^{2} = A K . A C$ . (2)

Từ (1) và (2) suy ra $H E^{2} = A K . A C$ (đpcm)

c) Xét tam giác ABC và tam giác NMC có:

$\hat{A} = \hat{N} (= 90^{\circ})$

$\hat{C}$ chung

Suy ra $Δ A B C ∽ Δ N M C (g . g)$ .

Do đó $\frac{C N}{A C} = \frac{C M}{B C}$ .

Xét tam giác BMC và tam giác ANC có:

$\frac{C N}{A C} = \frac{C M}{B C}$ (cmt)

$\hat{C}$ chung

Suy ra $Δ B M C ∽ Δ A N C (c . g . c)$ .

Do đó $\frac{B M}{B C} = \frac{A N}{A C}$ hay $A N = B M . \frac{A C}{B C}$ .

Trong tam giác vuông ABC, ta có: $\cos C = \frac{A C}{B C}$ .

Từ đó suy ra $A N = B M . \frac{A C}{B C} = B M . \cos C$ . (đpcm)

Câu 5:

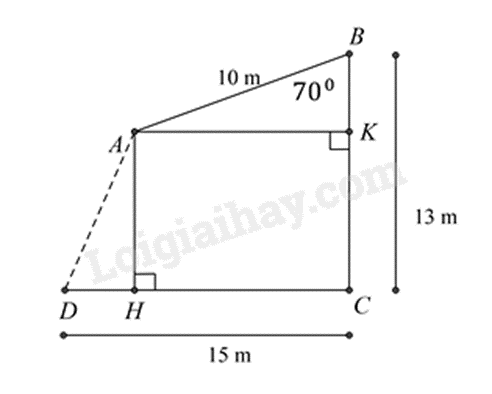
Bộ 10 đề thi giữa kì 1 Toán 9 Cánh diều có đáp án năm 2024 (ảnh 4)

Vẽ $A K ⊥ B C$ tại K, $A H ⊥ D C$ tại H, khi đó tứ giác $A K C H$ là hình chữ nhật.

Suy ra $A K = C H, A H = C K$

Trong tam giác vuông $A K B$ vuông tại $K$ có $A B = 10 c m$ , $\hat{A B K} = 70^{\circ}$

+) $A K = A B . \sin 70^{\circ} = 10. \sin 70^{\circ}$

Suy ra $A K = C H = 10. \sin 70^{\circ}$

Hay $D H = C D - H C = 15 - 10. \sin 70^{\circ}$

+) $B K = A B . \cos 70^{\circ} = 10. \cos 70^{\circ}$

Suy ra $C K = C B - B K = 13 - 10. \cos 70^{0}$

Hay $A H = C K = 13 - 10. \cos 70^{\circ}$

Theo định lí Pythagore trong tam giác vuông $A D H$ , ta có:

$A D = \sqrt{A H^{2} + D H^{2}} = \sqrt{{(13 - 10. \cos 70^{\circ})}^{2} + {(15 - 10. \sin 70^{\circ})}^{2}} \approx 11, 1 m$

Đề thi giữa kì 1 Toán 9 Cánh diều có đáp án - Đề 2

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Cánh diều

Năm học 2024 - 2025

Môn: Toán lớp 9

Thời gian làm bài: phút

(Đề số 2)

A. TRẮC NGHIỆM (3,0 điểm)

Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn

Trong mỗi câu hỏi từ câu 1 đến câu 4, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.

Câu 1. Mẫu thức chung khi quy đồng mẫu thức của phương trình $\frac{1}{x - 1} + \frac{3}{x^{2} - 1} + x = 0$ là

A. (x – 1)².

B. (x + 1)².

C. (x – 1)(x + 1).

D. x(x – 1)(x + 1).

Câu 2. Cho hệ phương trình $\{\begin{matrix} \frac{1}{2} x - \frac{1}{2} y = - 1 \\ - 3 x + 3 y = 5 \end{matrix}$ . Cho các khẳng định sau:

(i) Nhân phương trình thứ nhất của hệ với 6, rồi cộng với phương trình thứ hai ta được phương trình: 6y = –1.

(ii) Nhân phương trình thứ nhất của hệ với 6, rồi cộng với phương trình thứ hai ta được phương trình: 0x = –1.

(iii) Hệ phương trình đã cho vô nghiệm.

Số khẳng định đúng trong các khẳng định trên là

A. 0.

B. 1.

C. 2.

D. 3.

Câu 3. Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Khẳng định nào sau đây là đúng?

A. $\sin B = \frac{c}{a}$ .

B. $c = \frac{b}{\cot B}$ .

C. b = c.cosC.

D. c = b.tanC.

Câu 4. Cho tam giác ABC vuông tại A. Khẳng định nào sau đây là đúng?

A. AB² = BC² + AC².

B. sinC = cosB.

C. cotB – tanB = 0.

D. $\cot C = \frac{A C}{A B}$ .

Phần 2. Câu trắc nghiệm đúng sai

Trong câu 5, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).

Câu 5. Cho bất đẳng thức –5a > 3.

a) Số a có giá trị là một số âm.

b) Biểu thức 3 – 5a có giá trị là một số dương.

c) Biểu thức $a + \frac{3}{5}$ có giá trị là một số dương.

d) Biểu thức –10a – 10 có giá trị là một số âm.

Phần 3. Câu hỏi trắc nghiệm trả lời ngắn

Trong mỗi câu 6 và câu 7, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.

Câu 6. Tìm nghiệm của hệ phương trình $\{\begin{matrix} \frac{3}{2 x - y} - \frac{6}{x + y} = - 1 \\ \frac{1}{2 x - y} - \frac{1}{x + y} = 0 \end{matrix}$ .

Câu 7. Cho tam giác ABC vuông tại A có AB = 5 cm và đường cao AH = 3 cm. Tính số đo góc C (làm tròn kết quả đến phút).

B. TỰ LUẬN (7,0 điểm)

Bài 1. (2,5 điểm)

1. Giải các phương trình sau:

a) 4x(x + 3) – 3x – 9 = 0.

b) $\frac{x + 2}{x - 2} = \frac{x - 2}{x + 2} + \frac{16}{x^{2} - 4}$ .

2. Giải các bất phương trình sau:

a) 3x – 8 < 4x – 12.

b) 3(x – 2) – 5 > 3(2x – 1).

c) $\frac{4 x - 1}{2} + \frac{6 x - 19}{6} \geq \frac{9 x - 11}{3}$ .

Bài 2. (2,0 điểm)

1. Xác định a và b sao cho hệ phương trình $\{\begin{cases} a x + 2 b y = - 18 \\ b x - 3 a y = - 3 \end{cases}$ nhận cặp số (–3; 2) làm nghiệm.

2. Giải bài toán sau bằng cách lập hệ phương trình:

Một ôtô dự định đi từ A đến B trong khoảng thời gian nhất định. Nếu ôtô chạy nhanh hơn 10 km/h mỗi giờ thì đến nơi sớm hơn so với dự định là 3 giờ. Nếu ôtô chạy chậm hơn 10 km/h mỗi giờ thì đến nơi chậm mất so với dự định là 5 giờ. Tính vận tốc và thời gian dự định của ôtô.

Bài 3. (2,0 điểm)

1. Cho hình vẽ bên. Tính số đo góc α và các độ dài x, y (góc làm tròn đến độ và độ dài làm tròn đến hàng phần trăm).

10 Đề thi Giữa kì 1 Toán 9 Cánh diều (có đáp án + ma trận)

2. Tính chiều cao của một ngọn núi (kết quả làm tròn đến hàng đơn vị), biết tại hai điểm A, B cách nhau 500 m, người ta nhìn thấy đỉnh núi với góc nâng lần lượt là 34° và 38° (hình vẽ).

10 Đề thi Giữa kì 1 Toán 9 Cánh diều (có đáp án + ma trận)

Bài 4. (0,5 điểm) Cho tứ giác ABCD có α là góc nhọn tạo bởi hai đường chéo, chứng minh rằng:

$S_{A B C D} = \frac{1}{2} A C \cdot B D \cdot \sin α .$

-----HẾT-----

ĐÁP ÁN

A. TRẮC NGHIỆM (3,0 điểm)

Bảng đáp án trắc nghiệm:

Câu	1	2	3	4	5a	5b	5c	5d	6	7
Đáp án	C	C	D	B	Đ	Đ	S	S	(2; 1)	$\hat{C} \approx 53 ° 8^{'}$

B. TỰ LUẬN (7,0 điểm)

Bài 1. (2,5 điểm)

Hướng dẫn giải

1. a) 4x(x + 3) – 3x – 9 = 0

4x(x + 3) – 3(x + 3) = 0

(x + 3)(4x – 3) = 0

x + 3 = 0 hoặc 4x – 3 = 0

x = –3 hoặc x = $\frac{3}{4}$ .

Vậy phương trình đã cho có hai nghiệm là x = –3; x = $\frac{3}{4}$ .

1. b) Điều kiện xác định: x ≠ 2, x ≠ –2.

$\frac{x + 2}{x - 2} = \frac{x - 2}{x + 2} + \frac{16}{x^{2} - 4}$

$\frac{{(x + 2)}^{2}}{(x - 2) (x + 2)} = \frac{{(x - 2)}^{2}}{(x - 2) (x + 2)} + \frac{16}{(x - 2) (x + 2)}$

(x + 2)² = (x – 2)² + 16

x² + 4x + 4 = x² – 4x + 4 + 16

8x = 16

x = 2 (không thỏa mãn điều kiện)

Vậy phương trình đã cho vô nghiệm.

2. a) 3x – 8 < 4x – 12

3x – 4x < – 12 + 8

–x < –4

x > 4.

Vậy nghiệm của bất phương trình đã cho là x > 4.

2. b) 3(x – 2) – 5 > 3(2x – 1)

3x – 6 – 5 > 6x – 3

3x – 6x > – 3 + 6 + 5

–3x > 8

x < $- \frac{8}{3}$ .

Vậy nghiệm của bất phương trình đã cho là x < $- \frac{8}{3}$ .

2. c) $\frac{4 x - 1}{2} + \frac{6 x - 19}{6} \geq \frac{9 x - 11}{3}$

$\frac{3 (4 x - 1)}{6} + \frac{6 x - 19}{6} \geq \frac{2 (9 x - 11)}{6}$

3(4x – 1) + 6x – 19 ≥ 2(9x – 11)

12x – 3 + 6x – 19 ≥ 18x – 22

12x + 6x – 18x ≥ – 22 + 3 + 19

0x ≥ 0

Vậy nghiệm của bất phương trình đã cho là x ∈ ℝ.

Bài 2. (2,0 điểm)

Hướng dẫn giải

1. Để hệ phương trình $\{\begin{cases} a x + 2 b y = - 18 \\ b x - 3 a y = - 3 \end{cases}$ nhận cặp số (–3; 2) làm nghiệm thì x = –3 và y = 2 thỏa mãn hệ phương trình. Khi đó, ta có $\{\begin{cases} a \cdot (- 3) + 2 b \cdot 2 = - 18 \\ b \cdot (- 3) - 3 a \cdot 2 = - 3 \end{cases}$ hay $\{\begin{cases} - 3 a + 4 b = - 18 \\ - 6 a - 3 b = - 3 \end{cases}$ .

Nhân hai vế của phương trình thứ hai với $\frac{3}{4}$ ta được hệ phương trình mới $\{\begin{cases} - 3 a + 4 b = - 18 \\ - 8 a - 4 b = - 4 \end{cases}$ .

Cộng từng vế hai phương trình của hệ trên, ta được:

–11a = –22 suy ra a = 2.

Thay a = 2 vào phương trình –3a + 4b = –18, ta được:

–3.2 + 4b = –18, suy ra 4b = –12 nên b = –3.

Vậy a = 2 và b = –3.

2. Gọi x (km/h) là vận tốc dự định của ôtô và y (giờ) là thời gian dự định của ôtô để đi hết quãng đường AB (x > 10, y > 3).

– Quãng đường AB là xy (km).

– Nếu ôtô chạy nhanh hơn 10 km/h mỗi giờ thì đến nơi sớm hơn so với dự định là 3 giờ. Khi đó, ta có:

⦁ Vận tốc của ôtô lúc này là: x + 10 (km/h).

⦁ Thời gian ôtô đi hết quãng đường AB là: y – 3 (giờ).

⦁ Quãng đường AB là: (x + 10)(y – 3) (giờ).

Ta có phương trình: (x + 10)(y – 3) = xy

xy – 3x + 10y – 30 = xy

– 3x + 10y = 30 (1)

– Nếu ôtô chạy chậm hơn 10 km/h mỗi giờ thì đến nơi muộn hơn so với dự định là 5 giờ. Khi đó, ta có:

⦁ Vận tốc của ôtô lúc này là: x – 10 (km/h).

⦁ Thời gian ôtô đi hết quãng đường AB là: y + 5 (giờ).

⦁ Quãng đường AB là: (x – 10)(y + 5) (giờ).

Ta có phương trình: (x – 10)(y + 5) = xy

xy + 5x – 10y – 50 = xy

5x – 10y = 50 (2)

Từ phương trình (1) và phương trình (2) ta có hệ phương trình: $\{\begin{cases} - 3 x + 10 y = 30 \\ 5 x - 10 y = 50 \end{cases}$

Cộng từng vế hai phương trình của hệ, ta được: 2x = 80 suy ra x = 40 (thỏa mãn).

Thay x = 40 vào phương trình (1), ta được:

–3.40 + 10y = 30 hay 10y = 150 suy ra y = 15 (thỏa mãn).

Vậy vận tốc dự định của ôtô là 40 (km/h) và thời gian ôtô đi hết quãng đường AB là 15 (giờ).

Bài 3. (2,0 điểm)

Hướng dẫn giải

1. Xét ∆ABD vuông tại B, ta có:

$\tan \hat{B A D} = \frac{B D}{A B} = \frac{3}{5}$ , từ đó ta tìm được $α = \hat{B A D} \approx 31 °$ .

Suy ra $\hat{B A C} = \hat{B A D} + \hat{D A C} \approx 31 ° + 37 ° = 68 °$ .

Xét ∆ABC vuông tại B, ta có:

⦁ BC = $A B \cdot \tan \hat{B A C}$ $\approx 5 \cdot \tan 68 ° \approx 12,38$ , suy ra x = CD = BC – BD ≈ 12,38 – 3 = 9,38;

⦁ AB = $A C \cdot \cos \hat{B A C}$ suy ra y = AC = $\frac{A B}{\cos \hat{B A C}} \approx \frac{5}{\cos 68 °} \approx 13,35$ .

Vậy α ≈ 31°; x ≈ 9,38 và y ≈ 13,35.

2. Đặt: BC = x (m), khi đó AC = AB + BC = 500 + x (m).

Xét ∆ACD vuông tại C, ta có: CD = $A C \cdot tan \hat{C A D}$ = (500 + x).tan34°.

Xét ∆BCD vuông tại C ta có: CD = $B C \cdot tan \hat{C B D}$ = x.tan38°.

Do đó, ta có: (500 + x).tan34° = x.tan38°

500.tan34° + x.tan34° = x.tan38°

x.tan38° – x.tan34° = 500.tan34°

x(tan38° – tan34°) = 500.tan34°

x = $\frac{500 \cdot tan 34 °}{tan 38 ° - tan 34 °} \approx 3 158,5$ (m).

Suy ra CD = x.tan38° ≈ 3 158,5 . tan 38° ≈ 2 468 (m).

Vậy ngọn núi cao khoảng 2 468 mét.

Bài 4. (0,5 điểm)

Hướng dẫn giải

Gọi E là giao điểm của hai đường chéo AC và BD. Kẻ đường cao AH xuống BD và đường cao DK xuống AC.

Xét ∆AEH vuông tại H có: AH = AE.sinα.

Do đó $S_{A D E} = \frac{1}{2} D E \cdot A H = \frac{1}{2} D E \cdot A E \cdot \sin α$ .

Ta có: $\frac{S_{A D E}}{S_{A D C}} = \frac{\frac{1}{2} D K \cdot A E}{\frac{1}{2} D K \cdot A C} = \frac{A E}{A C}$

Suy ra $S_{A D C} = \frac{A C}{A E} \cdot S_{A D E}$ = $\frac{A C}{A E} \cdot \frac{1}{2} D E \cdot A E \cdot \sin α$ = $\frac{1}{2} D E \cdot A C \cdot \sin α .$