Bộ 10 đề thi giữa kì 1 Toán 9 Kết nối tri thức có đáp án năm 2024

Admin Vietjack Ngày: 25-09-2024 Lớp 9

2 K

Tailieumoi.vn xin giới thiệu bộ đề thi giữa kì 1 môn Toán lớp 9 sách Kết nối tri thức năm 2024 - 2025. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THCS dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi Giữa học kì 1 Toán 9. Mời các bạn cùng đón xem:

Đề thi giữa kì 1 Toán 9 Kết nối tri thức có đáp án năm 2024

Đề thi giữa kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 1

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Kết nối tri thức

Năm học 2024 - 2025

Môn: Toán lớp 9

Thời gian làm bài: phút

(Đề số 1)

I. Trắc nghiệm

Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1 : Nghiệm của phương trình $x + 2 y = 0$ là:

A. $(x; y) = (- 2; 1)$ .

B. $(x; y) = (1; 1)$ .

C. $(x; y) = (2; 1)$ .

D. $(- 1; - 1)$ .

Câu 2 : Hệ phương trình nào sau đây không phải hệ hai phương trình bậc nhất hai ẩn:

A.

${\begin{cases} 2 x - 3 y = 5 \\ x + 3 y = - 11 \end{cases}$ .
B.

${\begin{cases} 2 x - 3 y = 5 \\ 3 x = - 6 \end{cases}$ .
C.

${\begin{cases} 9 y = - 27 \\ x + 3 y = - 11 \end{cases}$ .
D.

${\begin{cases} x^{2} + y^{2} = 121 \\ x + 2 y = - 11 \end{cases}$ .

Câu 3 : Điều kiện xác định của phương trình $\frac{6}{x^{2} - 9} + \frac{2}{x - 3} = 0$

A.

$x \neq 0$ .
B.

$x \neq - 3; x \neq 3$ .
C.

$x \neq 0; x \neq 3$ .
D.

$x \neq 9$ .

Câu 4 : Phương trình $(2 x + 1) (x - 2) = 0$ có nghiệm là:

A.

$x = - \frac{1}{2}; x = - 2$ .
B.

$x = - \frac{1}{2}; x = 2$ .
C.

$x = \frac{1}{2}; x = - 2$ .
D.

$x = \frac{1}{2}; x = 2$ .

Câu 5 : Hệ thức nào sau đây là bất đẳng thức?

A.

$1 - x = 0$ .
B.

$x^{2} - 5 x + 6 = 0$ .
C.

$y^{2} \geq 0$ .
D.

$x = y$ .

Câu 6 : Với 3 số a, b, c và $a \geq b$ :

A.

nếu $c > 0$ thì $a c \leq b c$ .
B.

nếu $c < 0$ thì $a c > b c$ .
C.

nếu $c < 0$ thì $a c \geq b c$ .
D.

nếu $c > 0$ thì $a c \geq b c$ .

Câu 7 : Vế phải của bất phương trình $- 12 x + 5 \geq 6 - 11 x$ là:

A.

$- 12 x + 5$ .
B.

$- 12 x$ .
C.

$6$ .
D.

$6 - 11 x$ .

Câu 8 : Giá trị x thỏa mãn bất phương trình $- 2 x + 6 > 0$ là

A.

$x = 2$ .
B.

$x = 3$ .
C.

$x = 4$ .
D.

$x = 5$ .

Câu 9 : Cho tam giác ABC vuông tại B. Khi đó $\sin C$ bằng

A.

$\sin C = \frac{A B}{B C}$ .
B.

$\sin C = \frac{B C}{A C}$ .
C.

$\sin C = \frac{A C}{B C}$ .
D.

$\sin C = \frac{A B}{A C}$ .

Câu 10 : Cho tam giác ABC vuông tại A có $A C = 3 c m$ , $B C = 5 c m$ . Giá trị của cotB là

A.

$\frac{4}{3}$ .
B.

$\frac{3}{4}$ .
C.

$\frac{4}{5}$ .
D.

$\frac{5}{4}$ .

Câu 11 : Cho tam giác ABC vuông tại A có $A C = 6 c m$ , $B C = 12 c m$ . Số đo góc $A C B$ bằng

A.

$15^{\circ}$ .
B.

$30^{\circ}$ .
C.

$45^{\circ}$ .
D.

$60^{\circ}$ .

Câu 12 : Cho hình vẽ, độ dài cạnh BC là

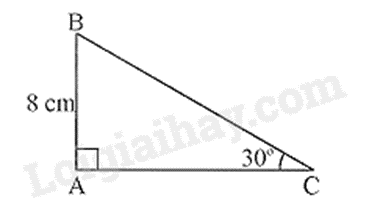
Bộ 10 đề thi giữa kì 1 Toán 9 Kết nối tri thức có đáp án năm 2024 (ảnh 1)

A.

$4 c m$ .
B.

$8 \sqrt{3} c m$ .
C.

$\frac{8 \sqrt{3}}{3} c m$ .
D.

$16 c m$ .

II. Tự luận

Câu 1 : 1. Giải các phương trình và bất phương trình sau:

a) $x^{2} - 5 x + 4 (x - 5) = 0$

b) $\frac{x}{x - 3} = \frac{x}{x + 3} + \frac{36}{x^{2} - 9}$

c) $3 x - 2 > 4$

d) $\frac{3 x - 1}{4} + 5 \leq \frac{x - 1}{2}$

2. Giải hệ phương trình ${\begin{cases} 2 x + y = 8 \\ x - y = - 5 \end{cases}$

Câu 2 : Giải bài toán bằng cách lập phương trình hoặc hệ phương trình

Bác An chia số tiền 600 triệu đồng của mình cho hai khoản đầu tư. Sau một năm, tổng tiền lãi thu được là 40 triệu đồng. Lãi suất cho khoản đầu tư thứ nhất là 6%/năm và khoản đầu tư thứ hai là 8%/năm. Tính số tiền bác An đầu tư cho mỗi khoản.

Câu 3 : Có thể em chưa biết: Cột cờ Hà Nội hay còn gọi Kỳ đài Hà Nội là một kết cấu dạng tháp được xây dựng cùng thời với thành Hà Nội dưới triều nhà Nguyễn (bắt đầu năm 1805, hoàn thành năm 1812). Kiến trúc cột cờ bao gồm ba tầng đế và một thân cột, được coi là một trong những biểu tượng của thành phố.

Đo chiều cao từ mặt đất đến đỉnh cột cờ của cột cờ Hà Nội (Kỳ đài Hà Nội), người ta cắm hai cọc bằng nhau MA và NB cao 1 m so với mặt đất. Hai cọc này song song, cách nhau 10 m và thẳng hàng so với tim cột cờ (như hình vẽ). Đặt giác kế đứng tại A và B để ngắm đến đỉnh cột cờ, người ta đo được các góc lần lượt là $50^{\circ} 19^{'} 12^{″}$ và $43^{\circ} 16^{'}$ so với đường song song mặt đất. Hãy tính chiều cao của cột cờ (làm tròn đến chữ số thập phân thứ hai)

Bộ 10 đề thi giữa kì 1 Toán 9 Kết nối tri thức có đáp án năm 2024 (ảnh 2)

Câu 4 : Cho tam giác ABC vuông tại B, đường cao BH. Vẽ HE vuông góc với AB, HF vuông góc với BC.

a) Tính BC, BH và $\hat{A C B}$ , biết $A B = 6 c m$ , $A C = 8 c m$ . (số đo góc làm tròn đến độ)

b) Chứng minh rằng: $B E . A B = B C^{2} - C H^{2}$ .

c) Chứng minh rằng: $B F = B E . \tan C$

Câu 5 : Cho $0 < a, b, c, d < 1$ . Chứng minh rằng:

$(1 - a) (1 - b) (1 - c) (1 - d) > 1 - a - b - c - d$ .

ĐÁP ÁN

I. Trắc nghiệm

1. A	2. D	3. B	4. B	5. C	6. D
7. D	8. A	9. D	10. B	11. D	12. D

II. Tự luận

Câu 1:

a) $x^{2} - 5 x + 4 (x - 5) = 0$

$\begin{array}{l} x (x - 5) + 4 (x - 5) = 0 \\ (x + 4) (x - 5) = 0 \end{array}$

+) $x + 4 = 0$ suy ra $x = - 4$

+) $x - 5 = 0$ suy ra $x = 5$

Vậy phương trình có nghiệm là $x = - 4; x = 5$ .

b) $\frac{x}{x - 3} = \frac{x}{x + 3} + \frac{36}{x^{2} - 9}$

ĐKXĐ: $x - 3 \neq 0$ ; $x + 3 \neq 0$ ; $x^{2} - 9 \neq 0$ hay $x \neq 3$ và $x \neq - 3$

Ta có: $\frac{x}{x - 3} = \frac{x}{x + 3} + \frac{36}{x^{2} - 9}$

$\begin{array}{l} \frac{x (x + 3)}{(x - 3) (x + 3)} = \frac{x (x - 3)}{(x + 3) (x - 3)} + \frac{36}{(x - 3) (x + 3)} \\ x (x + 3) = x (x - 3) + 36 \\ x^{2} + 3 x = x^{2} - 3 x + 36 \\ x^{2} - x^{2} + 3 x + 3 x = 36 \\ 6 x = 36 \\ x = 6 \end{array}$

Vậy nghiệm của phương trình là $x = 6$ .

c) $3 x - 2 > 4$

$\begin{array}{l} 3 x > 4 + 2 \\ 3 x > 6 \\ x > 2 \end{array}$

Vậy nghiệm của bất phương trình là $x > 2$ .

d) $\frac{3 x - 1}{4} + 5 \leq \frac{x - 1}{2}$

$\begin{array}{l} \frac{3 x - 1}{4} + \frac{20}{4} \leq \frac{2 (x - 1)}{4} \\ 3 x - 1 + 20 \leq 2 (x - 1) \\ 3 x + 19 \leq 2 x - 2 \\ 3 x - 2 x \leq - 2 - 19 \\ x \leq - 21 \end{array}$

Vậy nghiệm của bất phương trình là $x \leq - 21$ .

2. Giải hệ phương trình ${\begin{cases} 2 x + y = 8 \\ x - y = - 5 \end{cases}$

$\begin{array}{l} {\begin{cases} 2 x + y = 8 \\ x - y = - 5 \end{cases} \\ {\begin{cases} (2 x + x) + (y - y) = 8 + (- 5) \\ x - y = - 5 \end{cases} \\ {\begin{cases} 3 x = 3 \\ x - y = - 5 \end{cases} \\ {\begin{cases} x = 1 \\ 1 - y = - 5 \end{cases} \\ {\begin{cases} x = 1 \\ y = 6 \end{cases} \end{array}$

Vậy nghiệm của hệ phương trình là $(x; y) = (1; 6)$

Câu 2:

Gọi số tiền bác An đầu tư cho khoản thứ nhất là $x$ (triệu đồng),

số tiền bác An đầu tư cho khoản thứ hai là $y$ (triệu đồng), $(x, y > 0)$ .

Vì bác An chia số tiền 600 triệu đồng của mình cho hai khoản đầu tư nên ta có phương trình:

$x + y = 600$ . (1)

Vì lãi suất cho khoản đầu tư thứ nhất là 6%/năm và khoản đầu tư thứ hai là 8%/năm và sau một năm, tổng tiền lãi thu được là 40 triệu đồng nên ta có phương trình:

$6 % x + 8 % y = 40$ hay $0, 06 x + 0, 08 y = 40$ . (2)

Từ (1) và (2) ta có hệ phương trình: ${\begin{cases} x + y = 600 \\ 0, 06 x + 0, 08 y = 40 \end{cases}$ .

Từ phương trình (1), ta có: $y = 600 - x$ .

Thế vào phương trình (2), ta được phương trình mới: $0, 06 x + 0, 08 (600 - x) = 40$

Suy ra $0, 06 x + 0, 08 (600 - x) = 40$

$\begin{array}{l} 0, 06 x + 48 - 0, 08 x = 40 \\ - 0, 02 x = 40 - 48 \\ - 0, 02 x = - 8 \\ x = 400 \end{array}$

Suy ra $y = 600 - 400 = 200$ .

Vậy bác An đầu tư vào khoản thứ nhất 400 triệu đồng, khoản thứ hai 200 triệu đồng.

Câu 3:

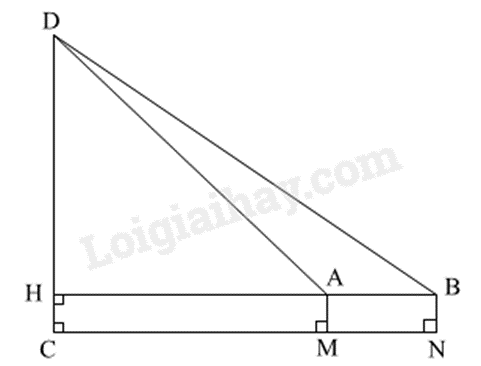
Bộ 10 đề thi giữa kì 1 Toán 9 Kết nối tri thức có đáp án năm 2024 (ảnh 3)

Kẻ DC là đoạn thẳng biểu diễn cột cờ, khi đó các cọc và cột cờ cùng vuông góc với mặt đất nên DC // AM // BN.

Xét tứ giác ABMN có AM // BN và AM = BN = 1 m nên ABMN là hình bình hành, suy ra $A B = M N = 10 m$ , AB // MN.

Kéo dài AB cắt DC tại H, mà AB // MN nên AH // CN.

Mà $D C ⊥ C N$ nên $D H ⊥ H B$ hay $\hat{D H B} = 90^{\circ}$ .

Xét tam giác DHA vuông tại H, ta có: $\cot D A H = \frac{A H}{D H}$ suy ra $A H = D H . \cot D A H$ .

Xét tam giác DHB vuông tại H, ta có: $\cot D B H = \frac{B H}{D H}$ suy ra $B H = D H . \cot D B H$ .

Ta có: $A B = B H - A H$

$A B = D H . \cot D B H - D H . \cot D A H$

$A B = D H (\cot D B H - \cot D A H)$

$10 = D H (\cot 43^{\circ} 16^{'} - \cot 50^{\circ} 19^{'} 12^{″})$

$D H = \frac{10}{\cot 43^{\circ} 16^{'} - \cot 50^{\circ} 19^{'} 12^{″}} \approx 42, 96 (m)$

Tứ giác AMCH có $\hat{M} = \hat{C} = \hat{H} = 90^{\circ}$ nên tứ giác AMCH là hình chữ nhật, suy ra $C H = A M = 1 m$ .

Vậy độ cao cột cờ DC là $D C = D H + H C = 42, 96 + 1 = 43, 96 (m)$ .

Câu 4:

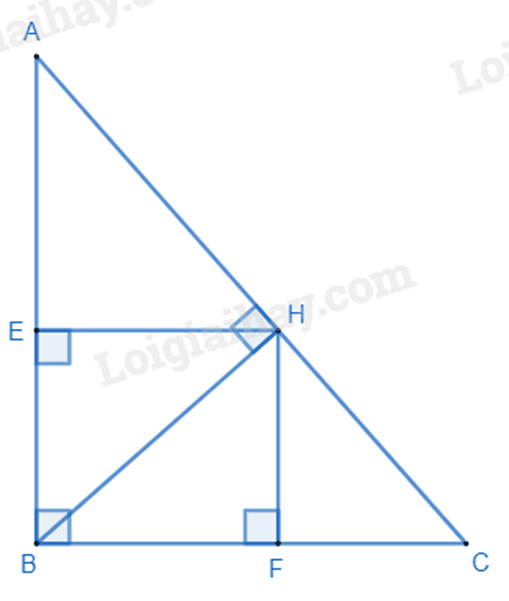
Bộ 10 đề thi giữa kì 1 Toán 9 Kết nối tri thức có đáp án năm 2024 (ảnh 4)

a) Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có:

$B C = \sqrt{A C^{2} - A B^{2}} = \sqrt{8^{2} - 6^{2}} = 2 \sqrt{7}$ (cm)

Áp dụng tỉ số lượng giác trong tam giác vuông ABC, ta có:

$\sin A C B = \frac{A B}{A C} = \frac{6}{8} = \frac{3}{4}$

Suy ra $\hat{A C B} \approx 49^{\circ}$

Xét tam giác ABH vuông tại H, ta có:

$\sin A C B = \frac{B H}{B C}$ suy ra $\frac{B H}{B C} = \frac{3}{4}$

Do đó $B H = \frac{3}{4} B C = \frac{3}{4} .2 \sqrt{7} = \frac{6 \sqrt{7}}{4}$ (cm)

b) Xét tam giác BEH và tam giác BHA có:

$\hat{B E H} = \hat{A H B} (= 90^{\circ})$

$\hat{B}$ chung

Suy ra $Δ B E H ∽ Δ B H A$ (g.g)

Suy ra $\frac{B E}{B H} = \frac{B H}{A B}$ , do đó $B E . A B = B H^{2}$ (1)

Áp dụng định lí Pythagore vào tam giác BHC vuông tại H, ta có:

$B C^{2} - H C^{2} = B H^{2}$ (2)

Từ (1) và (2) suy ra $B E . B A = B C^{2} - H C^{2}$ (đpcm)

c) Ta có $\hat{A B H} = \hat{C}$ (cùng phụ với $\hat{A}$ )

Xét tứ giác BEHF có $\hat{B} = \hat{E} = \hat{H} = 90^{\circ}$ nên tứ giác BEHF là hình chữ nhật, suy ra $H E = B F$ .

Xét tam giác BHE, ta có: $\tan H B E = \frac{E H}{E B}$ suy ra $E H = B E . \tan H B E$

Mà $\hat{H B E} = \hat{C}$ và $H E = B F$ (cmt) nên $B F = B E . \tan C$ (đpcm).

Câu 5:

Ta có: $(1 - a) (1 - b) = 1 - a - b + a b$ .

Vì $0 < a, b$ nên $1 - a - b + a b > 1 - a - b$ .

Vì $c < 1$ nên $1 - c > 0$ , suy ra $(1 - a) (1 - b) (1 - c) > (1 - a - b) (1 - c)$ .

Ta có: $(1 - a - b) (1 - c) = 1 - a - b - c + a c + b c$ .

Vì $0 < a, b, c$ nên $1 - a - b - c + a c + b c > 1 - a - b - c$ .

Lại có $d < 1$ nên $1 - d > 0$ , suy ra $(1 - a) (1 - b) (1 - c) (1 - d) > (1 - a - b - c) (1 - d)$

Ta có: $(1 - a - b - c) (1 - d) = 1 - a - b - c - d + a d + b d + c d$ .

Vì $0 < a, b, c, d$ nên $1 - a - b - c - d + a d + b d + c d > 1 - a - b - c - d$ .

Khi đó $(1 - a) (1 - b) (1 - c) (1 - d) > 1 - a - b - c - d$ .

Đề thi giữa kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 2

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Kết nối tri thức

Năm học 2024 - 2025

Môn: Toán lớp 9

Thời gian làm bài: phút

(Đề số 2)

A. TRẮC NGHIỆM (3,0 điểm)

Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn

Trong mỗi câu hỏi từ câu 1 đến câu 4, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.

Câu 1. Cặp số nào sau đây không phải là nghiệm của phương trình 2x – y – 1 = 0?

A. (1; 1).

B. (2; 3).

C. (1; –2).

D. (0; –1).

Câu 2. Hệ phương trình $\{\begin{cases} a x + b y = c \\ a^{'} x + b^{'} y = c^{'} \end{cases}$ có nhiều nhất bao nhiêu nghiệm?

A. 0.

B. 1.

C. 2.

D. Vô số.

Câu 3. Cho tam giác ABC vuông tại A có đường cao AH. Khi đó $\frac{H A}{H B}$ bằng

A. sinC.

B. cosC.

C. tanC.

D. cotC.

Câu 4. Cho α và β là hai góc nhọn bất kì thỏa mãn α + β = 90° và sinα = 0,5. Khẳng định nào sau đây là đúng?

A. sinβ = 0,5.

B. cosβ = 0,5.

C. tanβ = 0,5.

D. cotβ = 0,5.

Phần 2. Câu trắc nghiệm đúng sai

Trong câu 5, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).

Câu 5. Cho ba số a, b, c thỏa mãn a > b và c < 0.

a) ac < bc.

b) $\frac{a}{c} > \frac{b}{c}$ .

c) 2a – c > 2b – c.

d) c – 3a > c – 3b.

Phần 3. Câu hỏi trắc nghiệm trả lời ngắn

Trong mỗi câu 6 và câu 7, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.

Câu 6. Xác định hàm số y = ax + b để đồ thị của nó đi qua hai điểm A(–2; –1) và B(1; 4).

Câu 7. Cho tam giác ABC vuông tại A có AB = 5 cm và AC = 11 cm. Số đo góc B được làm tròn đến phút là bao nhiêu?

B. TỰ LUẬN (7,0 điểm)

Bài 1. (2,0 điểm) Giải các phương trình và bất phương trình sau:

a) (2x + 5)(1 – 4x) = 0.

b) $\frac{x + 4}{x + 1} - \frac{x + 1}{x - 4} = \frac{15 x}{x^{2} - 3 x - 4}$ .

c) 13 – 5x > –3x + 9.

d) $\frac{x + 1}{3} + \frac{2 x + 1}{4} \leq \frac{5 x + 3}{6} + \frac{7 + 12 x}{12}$ .

Bài 2. (2,5 điểm)

a) Tìm các hệ số x và y trong phản ứng hóa học đã được cân bằng sau:

xFe₃O₄ + O₂ → yFe₂O₃.

Từ đó, hãy hoàn thiện phương trình phản ứng hóa học sau khi được cân bằng.

b) Giải bài toán sau bằng cách lập hệ phương trình:

Khi cho hai vòi nước cùng chảy vào một bể cạn thì sau 1 giờ 20 phút sẽ đầy bể. Nếu mở vòi thứ nhất chảy trong 10 phút và mở vòi thứ hai chảy trong 12 phút thì sẽ được $\frac{2}{15}$ bể. Hỏi nếu chảy riêng, mỗi vòi nước sẽ chảy đầy bể trong bao lâu?

Bài 3. (2,5 điểm)

1) Bạn An muốn tính khoảng cách AB (làm tròn đến hàng phần mười của mét) ở hai bên hồ nước (hình vẽ). Biết rằng các khoảng cách từ một điểm C đến A và đến B là CA = 90 m, CB = 150 m và bạn ấy dùng giác kế đo được $\hat{A C B} = 120 °$ . Hãy tính AB giúp bạn An.

10 Đề thi Giữa kì 1 Toán 9 Kết nối tri thức (có đáp án + ma trận)