Tailieumoi.vn xin giới thiệu Đề cương ôn tập học kì 1 Toán 9 Kết nối tri thức năm 2024 – 2025. Tài liệu được biên soạn bởi đội ngũ giáo viên THPT dày dặn kinh nghiệm sẽ giúp các em làm quen với các dạng bài tập, nâng cao kỹ năng làm bài và rút kinh nghiệm cho bài thi học kì 1 Toán 9. Mời các bạn cùng đón xem:

Đề cương ôn tập học kì 1 Toán 9 Kết nối tri thức năm 2024

PHẦN I . NỘI DUNG ÔN TẬP

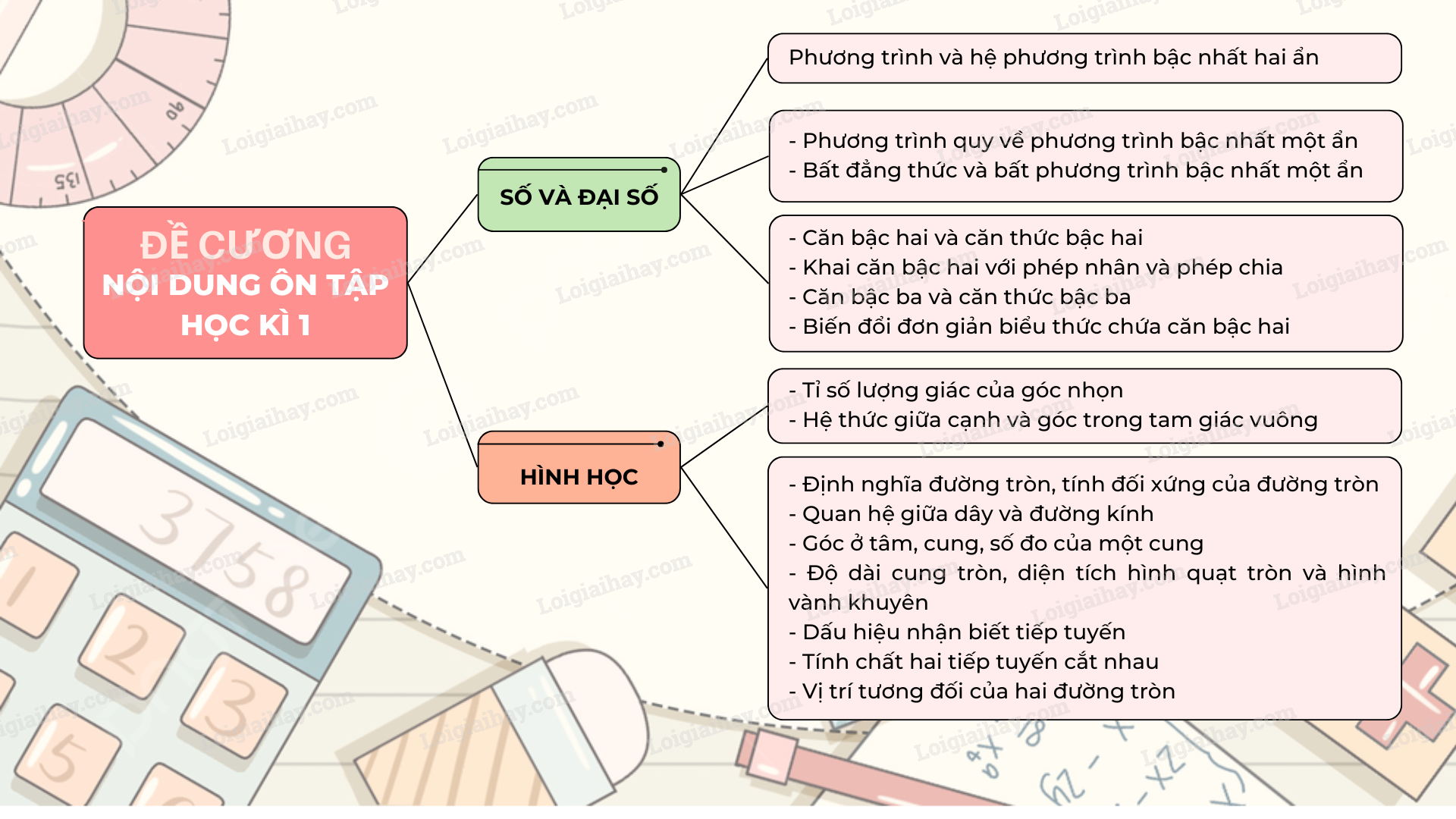
PHẦN II. BÀI TẬP

Đề bài

I. Phần trắc nghiệm

Câu 1: Phương trình nào sau đây là phương trình bậc nhất hai ẩn?

A. $xy+x=3$.

B. $x+y=xy$.

C. $2x-y=0$.

D. $x^2+y^2=5$.

Câu 2: Nghiệm của hệ phương trình $\{\begin{array}{l}-2x-y=-1\\ -x+2y=-1\end{array}$ là:

A. Hệ phương trình có nghiệm duy nhất.

B. Hệ phương trình vô nghiệm.

C. Hệ phương trình có hai nghiệm.

D. Hệ phương trình có vô số nghiệm.

Câu 3: Nghiệm của phương trình $\frac{x+1}{x-2}-1=\frac{24}{\left(x+3\right)\left(x-2\right)}$ là:

A. $x=2$.

B. $x=-3$.

C. $x=5$.

D. $x=-5$.

Câu 4: Nghiệm của phương trình $\left(x+5\right)\left(2x-10\right)=0$ là

A. $x=5$.

B. $x\ne 5$.

C. $x=-5$.

D. $x=-5;x=5$.

Câu 5: Số 3 là nghiệm của bất phương trình nào sau đây?

A. $5x-10\le 0$.

B. $2x+1>0$.

C. $-5x+7\ge 0$.

D. $2x-5<0$.

Câu 6: Giải phương trình: $x^2-\left(1+\sqrt{3}\right)x+\sqrt{3}=0$ 

A. $x=1;x=\sqrt{3}$.

B. $x=-1;x=\sqrt{3}$.

C. $x=1;x=-\sqrt{3}$.

D. $x=-1;x=-\sqrt{3}$.

Câu 7: Thực hiện phép tính:  $\sqrt{{\left(1-2\sqrt{3}\right)}^2}-\sqrt{4-2\sqrt{3}}$

A. $\sqrt{3}$.

B. $-\sqrt{3}$.

C. $\sqrt{2}$.

D. $-\sqrt{2}$.

Câu 8: Tính giá trị biểu thức $B=2\sqrt{2^2.5}-3\sqrt{3^2.5}+4\sqrt{4^2.5}.$

A. $B=9\sqrt{5}$.

B. $B=10\sqrt{5}$.

C. $B=11\sqrt{5}$.

D. $B=12\sqrt{5}$.

Câu 9: Biểu thức $\sqrt[3]{{\left(1-\sqrt{2018}\right)}^3}-\sqrt{2018}$ có giá trị bằng:

A. $1$.

B. $-1$.

C. $1-2\sqrt{2018}$.

D. $2\sqrt{2018}-1$.

Câu 10: Kết quả của $\sqrt[3]{{\left(x-1\right)}^3}$ là

A. $\frac{x-1}{3}$.

B. $1-x$.

C. $3\left(x-1\right)$.

D. $x-1$.

Câu 11: Cho tam giác ABC vuông tại A, có $AB=\frac{2}{3}BC$. Tính $\cot C$

A. $\cot C=\frac{3\sqrt{5}}{5}$.

B. $\cot C=\frac{\sqrt{5}}{2}$.

C. $\cot C=\frac{6}{5}$.

D. $\cot C=\frac{6\sqrt{5}}{5}$.

Câu 12: Cho tam giác ABC vuông tại A có $\hat{B}={30}^{\circ }$ và $AB=10cm$. Độ dài cạnh BC bằng bao nhiêu?

A. $10\sqrt{3}cm$.

B. $20\sqrt{3}cm$.

C. $\frac{10\sqrt{3}}{3}cm$.

D. $\frac{20\sqrt{3}}{3}cm$.

Câu 13: Cho tam giác MNP vuông tại M. Biết $MN=3cm,NP=5cm.$ Tỉ số lượng giác nào đúng?

A. $\cot P=\frac{3}{5}$.

B. $\tan P=\frac{5}{3}$.

C. $\sin P=\frac{3}{5}$.

D. $\cot P=\frac{3}{4}$.

Câu 14: Cho tam giác vuông ABC vuông tại $A$ như hình vẽ bên. Biết $\cos B=\frac{5}{8};$ độ dài trung tuyến AM bằng

A. $5cm$.

B. $4,5cm$.

C. $3,5cm$.

D. $4cm$.

Câu 15: Đường tròn tâm $O$ bán kính 5cm, $M$ là điểm nằm trên đường tròn đó khi và chỉ khi

A. $OM=5cm$.

B. $OM<5cm$.

C. $OM\ge 5cm$.

D. $OM\le 5cm$.

Câu 16: Trong đường tròn $\left(O;4cm\right)$, dây lớn nhất có độ dài bằng

A. 10cm.

B. 8cm.

C. 4cm.

D. 6cm.

Câu 17: Cho hai đường tròn $\left(O\right)$ và $\left(O^{\prime }\right)$ tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài $BC,B\in \left(O\right),C\in \left(O^{\prime }\right).$ Tiếp tuyến chung trong tại $A$ cắt tiếp tuyến chung ngoài BC ở I. Khi đó

A. $\widehat{BAC}={90}^{\circ }$.

B.  $\widehat{BAC}={60}^{\circ }$.

C. $\widehat{BAC}={30}^{\circ }$.

D.  $\widehat{BAC}={120}^{\circ }$.

Câu 18: Cho hai đường tròn $\left(O;2cm\right)$ và $\left(O^{\prime };6cm\right)$. Đường tròn $\left(O\right)$ và $\left(O^{\prime }\right)$ tiếp xúc ngoài với nhau khi OO' bằng:

A. 3cm.

B. 4cm.

C. 12cm.

D. 8cm.

Câu 19: Cho đường tròn $\left(O;R\right)$ có dây $MN=R\sqrt{2}$. Khi đó số đo của cung lớn MN là:

A. ${45}^{\circ }$.

B. ${90}^{\circ }$.

C. ${315}^{\circ }$.

D. ${270}^{\circ }$.

Câu 20: Ngũ giác đều ABCDE nội tiếp đường tròn tâm O. Khi đó góc COD bằng

A. ${18}^{\circ }$.

B. ${36}^{\circ }$.

C. ${55}^{\circ }$.

D. ${72}^{\circ }$.

II. Phần tự luận

Bài 1. Cho $A=\left(\frac{1}{\sqrt{x}+1}-\frac{2\sqrt{x}-2}{x\sqrt{x}-\sqrt{x}+x-1}\right):\left(\frac{1}{\sqrt{x}-1}-\frac{2}{x-1}\right)$ với $x\ge 0,x\ne 1.$

a) Rút gọn A.

b) Tìm$x\in \mathbb{Z}$ để $A\in \mathbb{Z}$.

c) Tìm x để A đạt GTNN.

Bài 2. Cho biểu thức $P=\frac{\sqrt{x}}{\sqrt{x}-2}+\frac{\sqrt{x}}{\sqrt{x}+2}-\frac{x-2\sqrt{x}}{x-4}$  và $Q=\frac{\sqrt{x}+2}{\sqrt{x}-2}\left(x\ge 0;x\ne 4\right)$

a) Rút gọn P.

b) Tính giá trị của P khi $x=16$.

c) Biết $M=P:Q$. Tìm giá trị của x để $M^2<\frac{1}{4}$.

Bài 3. Hôm qua mẹ của bạn An qua tiệm tạp hóa gần nhà mua $37$ quả trứng gồm $24$ quả trứng gà và $13$ quả trứng vịt hết $91200$ đồng. Hôm nay mẹ của bạn An cũng qua tiệm tạp hóa gần nhà mua $84$ quả trứng gồm $48$ quả trứng gà và $36$ quả trứng vịt hết $206400$ đồng. Hỏi nếu ngày mai mẹ bạn An nhờ bạn An qua tiệm tạp hóa trên mua $62$ quả trứng gồm $22$ quả trứng gà và $40$ quả trứng vịt thì mẹ bạn An phải đưa cho bạn An số tiền vừa đủ là bao nhiêu? (biết giá trứng không thay đổi)

Bài 4. Một trường trung học dự định tổ chức chuyến tham quan học tập thực tế cho học sinh khối 9 tại một bảo tàng và công viên khoa học (Science Park) trong 1 ngày (trong ngày từ 7h00 đến 17h00). Tổng kinh phí nhà trường dự trù là 20 triệu đồng, bao gồm chi phí thuê xe đưa đón và bữa ăn cho học sinh. Gọi $x$ là số bạn có thể tham gia chuyến tham quan. (học sinh, $x>0$)

• Giá thuê xe là 5 triệu đồng/ngày.
• Vé vào cổng mỗi học sinh là 30 000 đồng.
• Bữa ăn trưa cho mỗi học sinh có giá 50 000 đồng.

Trường có thể tổ chức cho tối đa bao nhiêu người?

Bài 5. Một đầu của cần gạt nước được cố định tại điểm O. Khi đầu còn lại của cần gạt xoay ${60}^{\circ }$, nó sẽ quét được một vùng có diện tích bằng $\frac{8}{3}\pi \left(m^2\right)$.

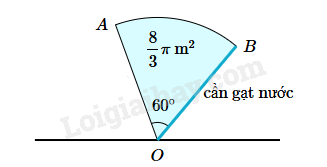
Chiều dài của cần gạt nước là bao nhiêu cm?

Bài 6. Một tấm bìa tạo bởi năm đường tròn đồng tâm lần lượt có bán kính $5\mathrm{c}\mathrm{m}$, $10\mathrm{c}\mathrm{m}$, $15\mathrm{c}\mathrm{m}$, $20\mathrm{c}\mathrm{m}$ và $30\mathrm{c}\mathrm{m}$. Giả thiết rằng người chơi ném phi tiêu một cách ngẫu nhiên và luôn trúng bia. Tính xác suất ném trúng vòng 8 (hình vành khuyên nằm giữa đường tròn thứ hai và thứ ba). Biết rằng xác suất cần tìm bằng tỉ số giữa diện tích của hình vành khuyên tương ứng với diện tích của hình tròn lớn nhất.

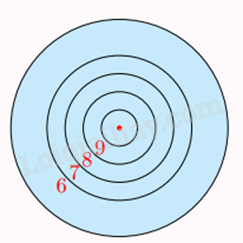
Bài 7. Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ các đường kính AOB, AO’C. Gọi DE là tiếp tuyến chung của hai đường tròn, $D\in \left(O\right)$ và $E\in \left(O^{\prime }\right)$. Gọi M là giao điểm của BD và CE.

a) Tính số đo của $\widehat{DAE}$.

b) Tứ giác ADME là hình gì?

c) Chứng minh MA là tiếp tuyến chung của hai đường tròn.

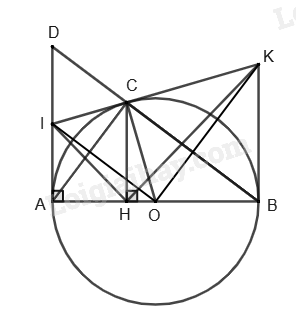
Bài 8. Cho đường tròn (O;R) đường kính AB và điểm C thuộc đường tròn (O) (C khác A và B). Kẻ CH vuông góc với AB tại H.

a) Chứng minh $\mathrm{\Delta }ABC$ vuông tại C và $C{H}^2=AC.BC.\sin A.\cos A$.

b) Tiếp tuyến tại A của đường tròn (O) cắt tia BC ở D. Gọi I là trung điểm của AD. Chứng minh đường thẳng IC là tiếp tuyến của đường tròn (O).

c) Tiếp tuyến tại B của đường tròn (O) cắt IC ở K. Xác định vị trí điểm C trên đường tròn (O) để diện tích tứ giác ABKI nhỏ nhất.

Bài 9. Để rào một khu đất có hai phần hình chữ nhật cho gia đình trồng hoa kiểng, một bác nông dân sử dụng 15 000 000 đồng để làm một cái hàng rào hình chữ E trước khuôn viên nhà dọc theo một con sông (như hình vẽ). Đối với mặt hàng rào song song với bờ sông thì chi phí nguyên vật liệu là 60 000 đồng/mét, còn đối với ba mặt hàng rào song song với nhau thì chi phí nguyên vật liệu là 50 000 đồng/mét.

Tính diện tích đất lớn nhất bác nông dân rào được.

Bài 10. Tính giá trị của $A=\frac{1}{2\sqrt{1}+1\sqrt{2}}+\frac{1}{3\sqrt{2}+2\sqrt{3}}+...+\frac{1}{2025\sqrt{2024}+2024\sqrt{2025}}$.

-------- Hết -------

Lời giải

I. Phần trắc nghiệm

 

Câu 1. C	Câu 2. A	Câu 3. C	Câu 4. D	Câu 5. B
Câu 6. A	Câu 7. A	Câu 8. C	Câu 9. C	Câu 10. D
Câu 11. B	Câu 12. D	Câu 13. C	Câu 14. D	Câu 15. A
Câu 16. B	Câu 17. A	Câu 18. D	Câu 19. D	Câu 20. B

 II. Phần tự luận

Bài 1. 

a) Với $x\ge 0,x\ne 1$ ta có:

$A=\left(\frac{1}{\sqrt{x}+1}-\frac{2\sqrt{x}-2}{x\sqrt{x}-\sqrt{x}+x-1}\right):\left(\frac{1}{\sqrt{x}-1}-\frac{2}{x-1}\right)$$A=\left(\frac{1}{\sqrt{x}+1}-\frac{2\sqrt{x}-2}{\left(x-1\right)\left(\sqrt{x}+1\right)}\right):\left(\frac{1}{\sqrt{x}-1}-\frac{2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)$

$A=\frac{x-1-2\sqrt{x}+2}{\left(x-1\right)\left(\sqrt{x}+1\right)}:\frac{\sqrt{x}+1-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}$

$A=\frac{x-2\sqrt{x}+1}{\left(x-1\right)\left(\sqrt{x}+1\right)}:\frac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}$

$A=\frac{{\left(\sqrt{x}-1\right)}^2}{\left(x-1\right)\left(\sqrt{x}+1\right)}.\left(\sqrt{x}+1\right)$

$A=\frac{{\left(\sqrt{x}-1\right)}^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}$

$A=\frac{\sqrt{x}-1}{\sqrt{x}+1}$.

b) Ta có $A=\frac{\sqrt{x}-1}{\sqrt{x}+1}=\frac{\sqrt{x}+1-2}{\sqrt{x}+1}=1-\frac{2}{\sqrt{x}+1},\left(x\ge 0\right).$

Đặt $B=\sqrt{x}+1$, để A nguyên khi x nguyên thì B là ước nguyên của 2.

Vì $x\ge 0$ nên $B>0$, suy ra B là ước nguyên dương của 2.

Ư$\left(2\right)=\left\{1;2\right\}$

TH1: $\sqrt{x}+1=1$ suy ra $x=0\left(tm\right)$

TH2: $\sqrt{x}+1=2$ suy ra $x=1\left(ktm\right)$

Vậy $x=0$ thì A nguyên.

c)  Ta có $A=\frac{\sqrt{x}-1}{\sqrt{x}+1}=1-\frac{2}{\sqrt{x}+1}$.

Vì $\sqrt{x}+1\ge 1\left(do\sqrt{x}\ge 0\right)$ nên  $\frac{2}{\sqrt{x}+1}\le \frac{2}{1}$

Suy ra $-\frac{2}{\sqrt{x}+1}\ge -2$

Do đó $1-\frac{2}{\sqrt{x}+1}\ge -1$ hay $A\ge -1$.

Dấu “=” xảy ra khi $x=0.$

Vậy $minA=-1$ khi $x=0$.

Bài 2. 

a) Ta có:

$P=\frac{\sqrt{x}}{\sqrt{x}-2}+\frac{\sqrt{x}}{\sqrt{x}+2}-\frac{x-2\sqrt{x}}{x-4}$

$P=\frac{\sqrt{x}}{\sqrt{x}-2}+\frac{\sqrt{x}}{\sqrt{x}+2}-\frac{\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}$

$P=\frac{\sqrt{x}}{\sqrt{x}-2}+\frac{\sqrt{x}}{\sqrt{x}+2}-\frac{\sqrt{x}}{\sqrt{x}+2}$

$P=\frac{\sqrt{x}}{\sqrt{x}-2}$.

b) Thay $x=16$ vào P, ta được:

$P=\frac{\sqrt{16}}{\sqrt{16}-2}=\frac{4}{4-2}=\frac{4}{2}=2$.

Vậy với $x=16$ thì $P=2$.

c) Ta có:

$M=P:Q=\frac{\sqrt{x}}{\sqrt{x}-2}:\frac{\sqrt{x}+2}{\sqrt{x}-2}$

$=\frac{\sqrt{x}}{\sqrt{x}-2}.\frac{\sqrt{x}-2}{\sqrt{x}+2}=\frac{\sqrt{x}}{\sqrt{x}+2}$

Vì $M^2<\frac{1}{4}$ nên ${\left(\frac{\sqrt{x}}{\sqrt{x}+2}\right)}^2<\frac{1}{4}$. Suy ra $\left|\frac{\sqrt{x}}{\sqrt{x}+2}\right|<\frac{1}{2}$

Vì $\sqrt{x}>0$ nên $\frac{\sqrt{x}}{\sqrt{x}+2}>0$

Do đó $\frac{\sqrt{x}}{\sqrt{x}+2}<\frac{1}{2}$

$2\sqrt{x}<\sqrt{x}+2$

$\sqrt{x}<2$

$x<4$

Kết hợp điều kiện $x\ge 0;x\ne 4$ ta được $0\le x<4$.

Vậy để $M^2<\frac{1}{4}$ thì $0\le x<4$.

Bài 3. 

Gọi giá tiền một quả trứng gà và một quả trứng vịt lần lượt là $x$ và $y$ đồng ($x;y\in \mathbb{N}$)

Vì mua $24$ quả trứng gà và $13$ quả trứng vịt hết $91200$ đồng nên ta có phương trình:

$24x+13y=91200$.

Vì mua $48$ quả trứng gà và $36$ quả trứng vịt hết $206400$ đồng nên ta có phương trình:

$48x+36y=206400$ hay $4x+3y=17200$.

Ta có hệ phương trình $\{\begin{array}{l}24x+13y=91200\\ 4x+3y=17200\end{array}$

$\begin{array}{l}\{\begin{array}{l}24x+13y=91200\\ 24x+18y=103200\end{array}\\ \{\begin{array}{l}5y=12000\\ 4x+3y=17200\end{array}\\ \{\begin{array}{l}y=2400\\ 4x+3.2400=17200\end{array}\\ \{\begin{array}{l}y=2400(TM)\\ x=2500(TM)\end{array}\end{array}$

Vậy số tiền mua $22$ quả trứng gà và $40$ quả trứng vịt là: $2500.22+2400.40=151000$ đồng.

Bài 4. 

Vì chuyến tham quan từ 7h00 đến 17h00, mỗi học sinh sẽ có chi phí vé vào cổng và bữa ăn trưa nên chi phí cho một học sinh đi tham quan là:

30 000 + 50 000 = 80 000 (đồng)

Tổng chi phí nhà trường phải trả bao gồm chi phí cho $x$ học sinh tham gia và chi phí thuê xe một ngày là:

80 000$x$+ 5 000 000 (đồng)

Vì tổng kinh phí nhà trường dự trù là 20 triệu đồng nên ta có bất phương trình:

$80000x+5000000\le 20000000$

Giải bất phương trình:

$80000x+5000000\le 20000000$

$80000x\le 15000000$ (cộng cả hai vế với $-5000000$)

$x\le \frac{15000000}{8000000}$ (nhân cả hai vế với $\frac{1}{80000}$)

$x\le 187,5$

Vì số học sinh phải là số nguyên nên số học sinh tối đa là 187.

Trường có thể tổ chức cho tối đa 187 học sinh tham gia chuyến tham quan này.

Bài 5. 

Vì diện tích hình quạt tròn là $\frac{8}{3}\pi$ nên ta có: $\frac{\pi .R^2.60}{360}=\frac{\pi R^2}{6}=\frac{8}{3}\pi$.

Suy ra $R^2=\frac{8}{3}\pi :\frac{\pi }{6}=16$.

Do đó $R=\sqrt{16}=4\left(m\right)$.

Vậy chiều dài của cần gạt nước là 4m.

Bài 6. 

Vì bán kính của đường tròn thứ hai và thứ ba lần lượt là 10cm và 15cm nên diện tích hình vành khuyên nằm giữa đường tròn thứ hai và thứ ba là:

$S_{vk}=\pi \left({15}^2-{10}^2\right)=125\pi \left(\mathrm{c}{\mathrm{m}}^2\right)$

Vì hình tròn lớn nhất có bán kính là 30cm nên diện tích hình tròn lớn nhất:

$S={30}^2\cdot \pi =900\pi \left(\mathrm{c}{\mathrm{m}}^2\right)$

Xác suất ném trúng vòng 8 là: $\frac{S_{vk}}{S}=\frac{125\pi }{900\pi }=\frac{5}{36}$

Vậy xác suất ném trúng vòng 8 là $\frac{5}{36}$.

Bài 7. 

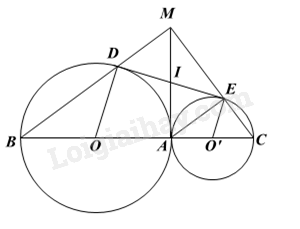
Từ A kẻ tiếp tuyến chung của hai đường tròn, tiếp tuyến này cắt DE tại I.

Theo tính chất hai tiếp tuyến cắt nhau, ta có ID = IA = IE nên $\mathrm{\Delta }DAE$ vuông tại A. Suy ra $\widehat{DAE}={90}^{\circ }$.

b) Vì AB và AC là các đường kính của (O) và (O’) nên $\widehat{ADB}=\widehat{AEC}={90}^{\circ }$.

Suy ra $\widehat{ADM}=\widehat{AEM}={90}^{\circ }$.

Mà $\widehat{DAE}={90}^{\circ }$ nên tứ giác ADME là hình chữ nhật.

c) Vì tứ giác ADME là hình chữ nhật nên 3 điểm M, I, A thẳng hàng.

Do vậy MA là tiếp tuyến chung của hai đường trong (O); (O’).

Bài 8. 

a) Vì AB là đường kính của (O) và $C\in \left(O\right)$ suy ra $\mathrm{\Delta }ABC$ vuông tại C.

Vì CH vuông góc với AB tại H nên theo hệ thức lượng trong tam giác vuông, ta có:

$CH=AC.\sin A$ (tam giác ACH vuông tại H)

và $CH=BC.\cos \widehat{HCB}$ (tam giác CHB vuông tại H).

Mà $\widehat{CAB}=\widehat{HCB}$ (cùng phụ với $\widehat{ACH}$) nên $\cos \widehat{CAB}=\cos \widehat{HCB}$ hay $\cos A=\cos \widehat{HCB}$. Do đó $CH=BC.\cos A$.

Do đó $C{H}^2=\left(AC.\sin A\right)\left(BC.\cos A\right)=AC.BC.\sin A.\cos A$.

b) Ta có $CI=IA=ID$ (đường trung truyến trong tam giác vuông)

Xét tam giác IAO và tam giác ICO có:

AO = OB = R

IA = IC (cmt)

OI chung

Suy ra $\mathrm{\Delta }IAO=\mathrm{\Delta }ICO\left(c.c.c\right)$, do đó $\widehat{IOA}=\widehat{ICO}={90}^{\circ }$ hay $IC\mathrm{\perp }OC$ tại C.

Vậy IC là tiếp tuyến của (O) tại điểm C.

c) Theo ý b, ta có $\mathrm{\Delta }AIO=\mathrm{\Delta }CIO$ (c.c.c).

Chứng minh tương tự, ta có $\mathrm{\Delta }KCO=\mathrm{\Delta }KBO$ (c.c.c).

Mà $S_{AIKB}=S_{\mathrm{\Delta }AIO}+S_{\mathrm{\Delta }CIO}+S_{\mathrm{\Delta }COK}+S_{\mathrm{\Delta }KOB}=2\left(S_{\mathrm{\Delta }CIO}+S_{\mathrm{\Delta }COK}\right)$

Suy ra $S_{AIKB}=2.S_{\mathrm{\Delta }IOK}=OC.IK=R.IK\ge R.AB=R.2R=2R^2$

Dấu “=” xảy ra khi IK = AB. Khi đó C là điểm chính giữa $\stackrel{⌢}{AB}$.

Vậy $S_{AIKB}$ có giá trị lớn nhất là $2R^2$ khi C là điểm chính giữa $\stackrel{⌢}{AB}$.

Bài 9. 

Gọi độ dài của hàng rào song song với bờ sông là $x\left(m,x>0\right)$;

độ dài của mỗi hàng rào trong ba hàng rào song song nhau là $y\left(m,y>0\right)$.

Diện tích đất mà bác nông dân rào được là: $xy\left(m^2\right)$.

Tổng chi phí là 15 000 000 đồng nên ta có phương trình:

$60000.x+50000.3y=15000000$

hay $6x+15y=1500$ (1)

Áp dụng bất đẳng thức Cauchy cho hai số dương ta có:

$6x+15y\ge 2\sqrt{6x.15y}=2\sqrt{90xy}$ (2)

Từ (1) và (2) suy ra:

$2\sqrt{90xy}\le 1500$

$\sqrt{90xy}\le 750$ (nhân cả hai vế với $\frac{1}{2}$)

$90xy\le {750}^2$ hay $90xy\le 562500$

Suy ra $xy\le \frac{562500}{90}$ hay $xy\le 6250$

Dấu “=” xảy ra là giá trị lớn nhất của $xy$. Do đó $xy$ lớn nhất bằng $6250$.

Vậy diện tích lớn nhất mà bác nông dân có thể rào là $6250m^2$.

Bài 10. 

Ta có:

$\begin{array}{l}k\sqrt{k-1}+\left(k-1\right)\sqrt{k}\\ =\sqrt{k}.\sqrt{k-1}.\left(\sqrt{k}+\sqrt{k-1}\right)\end{array}$

$=\sqrt{k\left(k-1\right)}\left(\sqrt{k}+\sqrt{k-1}\right)$ với $k\ge 1$.

Suy ra

$\begin{array}{l}\frac{1}{k\sqrt{k-1}+\left(k-1\right)\sqrt{k}}\\ =\frac{1}{\sqrt{k\left(k-1\right)}\left(\sqrt{k}+\sqrt{k-1}\right)}\\ =\frac{\left(\sqrt{k}-\sqrt{k-1}\right)}{\sqrt{k\left(k-1\right)}\left(\sqrt{k}+\sqrt{k-1}\right)\left(\sqrt{k}-\sqrt{k-1}\right)}\end{array}$

$\begin{array}{l}=\frac{\sqrt{k}-\sqrt{k-1}}{\sqrt{k\left(k-1\right)}}\\ =\frac{\sqrt{k}-\sqrt{k-1}}{\sqrt{k}.\sqrt{k-1}}\\ =\frac{1}{\sqrt{k-1}}-\frac{1}{\sqrt{k}}\end{array}$ 

Thay lại vào A ta được:

$A=\frac{1}{2\sqrt{1}+1\sqrt{2}}+\frac{1}{3\sqrt{2}+2\sqrt{3}}+...+\frac{1}{2025\sqrt{2024}+2024\sqrt{2025}}$$=\left(\frac{1}{\sqrt{1}}-\frac{1}{\sqrt{2}}\right)+\left(\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{3}}\right)+.....+\left(\frac{1}{\sqrt{2024}}-\frac{1}{\sqrt{2025}}\right)$

$=1-\frac{1}{\sqrt{2025}}=1-\frac{1}{45}=\frac{44}{45}$.

Vậy $A=\frac{44}{45}$.

PHẦN III. ĐỀ MINH HỌA

A. TRẮC NGHIỆM (2,0 điểm)

Câu 1. Phương trình nào sau đây không là phương trình bậc nhất hai ẩn?

A. $\frac{x}{2}+\frac{y}{3}=4$.

B. 3x - 0y - 2 = 0.

C. $3y-2z=\frac{1}{2}$.

D. $\frac{2}{x}+\frac{y}{3}-2=0$.

Câu 2. Điều kiện xác định của phương trình $\frac{x+2}{x-4}-1=\frac{30}{\left(x+3\right)\left(x-4\right)}$ là

A. x ≠ -3; x ≠ 4.

B. x ≠ 3; x ≠ -4.

C. x ≠ -3; x ≠ 4; x ≠ -2.

D. x ≠ -3; x ≠ -4.

Câu 3. Bất đẳng thức diễn tả khẳng định “ n nhỏ hơn $\frac{3}{5}$” là

A. $n\le \frac{3}{5}$.

B. $n<\frac{3}{5}$.

C. $n>\frac{3}{5}$.

D. $n\ge \frac{3}{5}$.

Câu 4. Điều kiện xác định của biểu thức A = $\sqrt{1-2x}$ là

A. $x\le \frac{1}{2}$.

B. $x<\frac{1}{2}$.

C. $x>\frac{1}{2}$.

D. $x\ge \frac{1}{2}$.

Câu 5. Cho $\sin x=\frac{1}{2}$ khi đó cos x bằng

A. $\frac{\sqrt{3}}{2}$.

B. $\sqrt{3}$.

C. $\frac{1}{2}$.

D. $\frac{\sqrt{2}}{2}$.

Câu 6. Cho tam giác ABC vuông tại A có BC = 8 cm, AC = 6 cm. Tỉ số lượng giác C là bao nhiêu? (kết quả được làm tròn đến hàng phần trăm)

A. 0,87.

B. 0,86.

C. 0,88.

D. 0,89.

Câu 7. Điểm M nằm trên đường tròn (O; R) nếu

A. OM = R.

B. OM > R.

C. OM < R.

D. OM = 2R.

Câu 8. Cung có số đo 110° của đường tròn bán kính 8 cm dài bao nhiêu? (làm tròn kết quả đến hàng phần chục)

A. 15,3 cm.

B. 14,5 cm.

C. 15,5 cm.

D. 15 cm.

B. TỰ LUẬN (8,0 điểm)

Bài 1. (2,0 điểm)

Cho biểu thức $A=\frac{x-7}{\sqrt{x}}$ và $B=\frac{1}{\sqrt{x}+2}+\frac{\sqrt{x}}{2-\sqrt{x}}+\frac{2x-\sqrt{x}+2}{x-4}$ với x > 0, x ≠ 4.

a) Tính giá trị của A khi x = 9.

b) Rút gọn biểu thức B.

c) Tìm tất cả các giá trị nguyên của x để biểu thức P = A.B có giá trị nguyên.

Bài 2. (2,0 điểm)

1. Giải các phương trình, bất phương trình sau:

a) $\frac{2}{x-2}-\frac{3}{x-3}=\frac{3x-20}{\left(x-3\right)\left(x-2\right)}$.

b) $5x-4-3\left(2x-9\right)\le 5x-8$.

2. Giải bài toán bằng cách lập hệ phương trình.

Một đội công nhân A và B làm chung một công việc và dự định hoàn thành trong 12 ngày. Khi làm chung được 8 ngày thì đội A được điều động đi làm việc khác, đội B tăng gấp đôi năng suất, do đó đội B đã hoàn thành phần việc còn lại trong 8 ngày tiếp theo. Hỏi với năng suất ban đầu thì mỗi đội làm một mình sẽ hoàn thành công việc đó trong bao lâu?

Bài 3. (1,0 điểm) Một người có tầm mắt cao 1,65 m đứng trên tầng thượng của tòa Lotte Center thì nhìn thấy một chiếc xe thu gom phế thải đang dừng ở B với góc nghiêng 80° (như hình vẽ). Biết xe đó cách tòa nhà 48 m. a) Tính chiều cao của tòa nhà Lotte Center. b) Một người ở độ cao 200 m của tòa nhà cũng nhìn thấy xe thu gom phế thải khác đang dừng ở E với góc nghiêng 65°. Hỏi hai xe thu gom phế thải cách nhau bao nhiêu mét? (tất cả các kết quả làm tròn đến hàng phần trăm)

Bài 4. (2,5 điểm) Cho đường tròn (O;R) và điểm A nằm ngoài đường tròn (O). Từ A vẽ hai tiếp tuyến AB và AC của đường tròn (O) (B, C là hai tiếp điểm). Gọi H là giao điểm của OA và BC. Từ B vẽ đường kính BD của (O), đường thẳng AD cắt (O) tại E (E khác D).

a) Chứng minh rằng OA ⊥ BC tại H.

b) Chứng minh $\widehat{ABE}=\widehat{ADB}$ và AE.AD = AB².

c) Cho biết OA = $\left(\sqrt{6}+\sqrt{2}\right)R$, tính diện tích hình quạt giới hạn bởi bán kính OC, OD và cung nhỏ CD.

Bài 5. (0,5 điểm) Bạn Nam làm một căn nhà đồ chơi bằng gỗ có phần mái là một chóp tứ giác đều. Biết các cạnh bên của mái nhà bạn Nam dùng các thanh gỗ có chiều dài 16 cm. Bạn Nam dự định dùng giấy màu để phủ kín phần mái nhà. Gọi độ dài cạnh đáy của phần mái là 2x (cm). Hỏi diện tích giấy màu cần sử dụng nhiều nhất là bao nhiêu?

------HẾT------

ĐÁP ÁN & HƯỚNG DẪN GIẢI

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)

B. TỰ LUẬN (8,0 điểm)

Bài 1. (2,0 điểm)

a) Thay x = 9 (thỏa mãn điều kiện) vào biểu thức A, ta có:

A = $\frac{9-7}{\sqrt{9}}=\frac{2}{3}$.

Vậy $A=\frac{2}{3}$ khi x = 9.

b) Với x > 0, x ≠ 4, ta có:

c) Ta có: P = A.B với x > 0, x ≠ 4.

P = $\frac{x-7}{\sqrt{x}}.\frac{\sqrt{x}}{\sqrt{x}+2}=\frac{x-7}{\sqrt{x}+2}$.

Xét P = 0 thì $\frac{x-7}{\sqrt{x}+2}=0$, suy ra x - 7 = 0 khi x = 7 (thỏa mãn).

Xét P ≠ 0, ta có:

Vì $\sqrt{x}+2>0$ nên $\left(\sqrt{x}+2\right)\in \left\{1;3\right\}$.

Nhận thấy $\sqrt{x}+2\ge 0$ nên $\sqrt{x}+2=3$ nên $\sqrt{x}=1$, do đó x = 1 (thỏa mãn).

Vậy với x ∈ {1;7} thì P có giá trị nguyên.

Bài 2. (2,0 điểm)

2. Gọi x, y (ngày) lần lượt là số ngày đội A và đội B làm một mình để hoàn thành công việc (x, y > 0).

Trong một ngày đội A làm được $\frac{1}{x}$ công việc, đội B làm được $\frac{1}{y}$ công việc.

Trong một ngày, hai đội làm chung được số phần công việc là: $\frac{1}{x}+\frac{1}{y}$ (công việc).

Trong 8 ngày, số phần công việc hai đội làm được là: $8\left(\frac{1}{x}+\frac{1}{y}\right)$ (công việc).

Sau 8 ngày, phần công việc còn lại là: $1-8\left(\frac{1}{x}+\frac{1}{y}\right)$ (công việc).

Theo đề bài, khi làm một mình đội B tăng gấp đôi năng suất. Lúc này, trong 1 ngày, đội B làm được: $2.\frac{1}{y}=\frac{2}{y}$ (công việc).

Trong 8 ngày tiếp theo, đội B đã hoàn thành phần việc còn lại, nên ta có phương trình:

$1-8\left(\frac{1}{x}+\frac{1}{y}\right)=8.\frac{2}{y}$ hay $\frac{8}{x}+\frac{24}{y}=1$         (1).

Mà ban đầu hai đội dự định hoàn thành công việc trong 12 ngày khi làm chung. Do đó, ta có phương trình:

$12\left(\frac{1}{x}+\frac{1}{y}\right)=1$ hay $\frac{1}{x}+\frac{1}{y}=\frac{1}{12}$              (2).

Từ (1) và (2), ta có hệ phương trình sau: $\left\{\begin{array}{l}\frac{1}{x}+\frac{1}{y}=\frac{1}{12}\\ \frac{8}{x}+\frac{24}{y}=1\end{array}\right.$.

Từ phương trình thứ hai của hệ, ta có $\frac{1}{x}=\frac{1}{12}-\frac{1}{y}$ vào phương trình (1), ta được:

$8\left(\frac{1}{12}-\frac{1}{y}\right)+\frac{24}{y}=1$ hay $\frac{2}{3}+\frac{16}{y}=1$ suy ra $\frac{16}{y}=\frac{1}{3}$ khi y = 48 (TMĐK).

Thay y = 48 vào phương trình (2) suy ra $\frac{1}{x}=\frac{1}{12}-\frac{1}{48}=\frac{1}{16}$, suy ra x = 16 (TMĐK).

Vậy đội A làm một mình sẽ hoàn thành công việc trong 16 ngày, đội B làm một mình sẽ hoàn thành công việc trong 48 ngày.

Bài 3. (1,0 điểm)

a) Từ hình vẽ, ta xét tam giác vuông ABC, có:

AC = $AB.\tan \widehat{CBA}=48.\tan 80°\approx \mathrm{272,22}$ (m). 

Do người đó có tầm mắt 1,65 m nên chiều cao của tòa nhà là:

272,22 - 1,65 = 270,57 (m).

Vậy tòa nhà cao 270,57 m.

b) Khoảng cách từ xe thu gom phế thải ở E đến chân tòa nhà là độ dài đoạn EA.

Xét tam giác vuông EAD, ta có:

EA = $\frac{AD}{\tan \widehat{DEA}}=\frac{200}{\tan 65°}\approx \mathrm{93,26}$ (m). 

Khoảng cách của hai xe phế thải là 93,26 - 48 = 45,26 (m).

Vậy hai xe phế thải cách nhau 45,26 m.

Bài 4. (2,5 điểm)

a) Xét đường tròn (O) có: AB, AC lần lượt là tiếp tuyến tại B, C nên AB = AC (tính chất hai tiếp tuyến cắt nhau) . Suy ra A thuộc đường trung trực của BC. Mà OB = OC = R nên O thuộc đường trung trực của BC Do đó OA là đường trung trực của BC nên OA ⊥ BC tại H. b) Xét ∆OBE cân tạo O (do OB = OE = R) nên $\widehat{OBE}=\widehat{OEB}=\frac{180°-\widehat{BOE}}{2}=90°-\frac{1}{2}\widehat{BOE}$.

c) Xét ∆AOB vuông tại B, có:

$\cos \widehat{AOB}=\frac{OB}{OA}=\frac{R}{\left(\sqrt{6}+\sqrt{2}\right)R}=\frac{\sqrt{6}-\sqrt{2}}{4},$ suy ra $\widehat{AOB}=75°$.

Do AB, AC lần lượt là tiếp tuyến tại B, C của đường tròn (O) nên OA là tia tiếp tuyến của $\widehat{BOC}$ (tính chất 2 tiếp tuyến cắt nhau).

Suy ra $\widehat{BOC}=2\widehat{AOB}=2\cdot 75°=150°$.

Do đó $\widehat{COD}=180°-\widehat{BOC}=180°-150°=30°$ nên $\text{sđ}\stackrel{⏜}{CD}=30°$.

Diện tích hình quạt giới hạn bởi bán kính OC, OD và cung nhỏ CD là:

$S=\frac{\pi R^2\cdot 30}{360}=\frac{\pi R^2}{12}$ (đvdt).

Vậy diện tích hình quạt giới hạn bởi bán kính OC, OD và cung nhỏ CD là $\frac{\pi R^2}{12}$ (đvdt).

Bài 5. (0,5 điểm)

Diện tích giấy màu cần sử dụng chính bằng tổng diện tích bốn mặt bên là các tam giác cân có cạnh bên bằng 16 cm và cạnh đáy là 2x (cm).

Xét tam giác SBC, kẻ đường cao SH ⊥ BC tại H.

Do tam giác SBC cân tại S nên SH vừa là đường cao, vừa là đường trung trực suy ra H là trung điểm của BC.

Suy ra BH = HC = $\frac{BC}{2}$ = x (cm)  (0 < x < 16).

Áp dụng định lí Pythagore vào tam giác SHC, ta có: $S{H}^2+H{C}^2=S{C}^2$

Suy ra $S{H}^2={16}^2-x^2=256-x^2$.

Do đó $SH=\sqrt{256-x^2}$.

Diện tích tam giác SBC là $\frac{1}{2}.2x.\sqrt{256-x^2}=x\sqrt{256-x^2}\left({\text{cm}}^2\right)$.

Diện tích giấy màu cần sử dụng là $4x\sqrt{256-x^2}\left({\text{cm}}^2\right)$.

Thực hiện tính giá trị lớn nhất của $S=4x\sqrt{256-x^2}$ với 0 < x < 16.

Ta có: $4x\sqrt{256-x^2}=4\sqrt{256x^2-x^4}$

                              = $4\sqrt{-\left(x^4-2.128x^2+{128}^2\right)+{128}^2}$

                              = $4\sqrt{-{\left(x^2-128\right)}^2+{128}^2}$.

Vì ${\left(x^2-128\right)}^2\ge 0$ với mọi x ∈ ℝ nên $-{\left(x^2-128\right)}^2\le 0$ với mọi x ∈ ℝ.

Suy ra $4\sqrt{-{\left(x^2-128\right)}^2+{128}^2}\le 4\sqrt{{128}^2}=512$ với mọi x ∈ ℝ.

Do đó, $S=4x\sqrt{256-x^2}\le 512$ với mọi x ∈ ℝ.

Dấu "=" xảy ra khi x² - 128 = 0 hay $x=8\sqrt{2}\left(0<x<16\right)$.

Vậy diện tích giấy màu cần sử dụng nhiều nhất là 512 cm².