Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 9 Tính chất của phép khai phương được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Tính chất của phép khai phương. Mời các bạn đón xem:

Bài tập Toán 9 Tính chất của phép khai phương

A. Bài tập Tính chất của phép khai phương

Bài 1. Tính:

Hướng dẫn giải

a) Ta có: $\sqrt{{\left(-9\right)}^2}=\left|-9\right|=9.$

b) Ta có: $\sqrt{{\left(-\frac{6}{7}\right)}^2}=\left|-\frac{6}{7}\right|=\frac{6}{7}.$

c) Ta có: ${\left(-\sqrt{3}\right)}^2-\sqrt{36}=3-6=-3.$

d) ${\left(\sqrt{\frac{4}{9}}\right)}^2.\sqrt{0,81}=\frac{4}{9}.0,9=\frac{4}{9}.\frac{9}{10}=\frac{2}{5}.$

Bài 2. Rút gọn các biểu thức sau:

a) $\sqrt{7^2.5};$

b) $\sqrt{100a^2}$ với a < 0;

c) $\sqrt{6b}.\sqrt{24b}-4b$ với b ≥ 0.

Hướng dẫn giải

a) Ta có: $\sqrt{7^2.5}=7\sqrt{5}.$

b) Ta có: $\sqrt{100a^2}=\sqrt{{\left(10a\right)}^2}=\left|10a\right|=-10a$ với a < 0.

c) Với b ≥ 0, ta có:

$\sqrt{6b}.\sqrt{24b}-4b=\sqrt{6b.24b}-4b=\sqrt{144b^2}-4b$

$=\sqrt{{\left(12b\right)}^2}-4b=\left|12b\right|-4b=12b-4b=8b$

Bài 3. Cho hình chữ nhật có chiều rộng a (cm), chiều dài b (cm) và diện tích S (cm²).

a) Tìm S, biết $a=\sqrt{6},$ $b=\sqrt{48};$

b) Tìm a, biết $S=5\sqrt{6},$ $b=\sqrt{3}.$

Hướng dẫn giải

a) Ta có: S = a.b

$=\sqrt{6}.\sqrt{48}$$=\sqrt{6.48}$

=$\sqrt{288}$$=12\sqrt{2}$

Vậy $S=12\sqrt{2}$ cm².

b) Ta có: a = S : b

$=5\sqrt{6}:\sqrt{3}$

$=5\sqrt{\frac{6}{3}}$$=5\sqrt{2}$

Vậy $a=5\sqrt{2}$cm

B. Lý thuyết Tính chất của phép khai phương

1. Căn thức bậc hai của một bình phương

Tính chất

Ví dụ: Với $x<0$, ta có 1 – x > 0. Do đó ${\left(\sqrt{1-x}\right)}^2=1-x$.

2. Căn thức bậc hai của một tích

Ví dụ:

$\sqrt{27}.\sqrt{3}=\sqrt{27.3}=\sqrt{81}=9$

Với $a\ge 0,b<0$ thì $\sqrt{25a^2{b}^2}=\sqrt{5^2.a^2.{\left(-b\right)}^2}=\sqrt{5^2}.\sqrt{a^2}.\sqrt{{\left(-b\right)}^2}=5.a.\left(-b\right)=-5ab$.

Nhận xét: Ta có thể biến đổi $\sqrt{ab}=\sqrt{a}.\sqrt{b}$ hoặc $\sqrt{a}.\sqrt{b}=\sqrt{ab}$ ($a\ge 0$ và $b\ge 0$) để việc tính toán được dễ dàng hơn.

Tổng quát, với hai biểu thức A và B mà $B\ge 0$, ta có $\sqrt{A^{2}B}=\left|A\right|\sqrt{B}$.

Ví dụ:

$\sqrt{75}=\sqrt{25.3}=\sqrt{5^2.3}=5\sqrt{3}$

$\sqrt{15a}.\sqrt{3a}=\sqrt{15a.3a}=\sqrt{3^2{a}^2.5}=\left|3a\right|\sqrt{5}$.

2. Căn thức bậc hai của một thương

Tính chất

Ví dụ: $\sqrt{\frac{49}{64}}=\frac{\sqrt{49}}{\sqrt{64}}=\frac{7}{8}$;

$\sqrt{\frac{4a^2}{25}}=\frac{\sqrt{4a^2}}{\sqrt{25}}=\frac{\sqrt{4}.\sqrt{a^2}}{\sqrt{25}}=\frac{2\left|a\right|}{5}$;

$\frac{\sqrt{8}}{\sqrt{2}}=\sqrt{\frac{8}{2}}=\sqrt{4}=2$;

Với $a>0$ thì $\frac{\sqrt{52a^3}}{\sqrt{13a}}=\sqrt{\frac{52a^3}{13a}}=\sqrt{4a^2}=\sqrt{{\left(2a\right)}^2}=2a$.

Nhận xét: Ta có thể biến đổi $\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$ hoặc $\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}$ ($a\ge 0$ và $b\ge 0$) để việc tính toán được dễ dàng hơn.

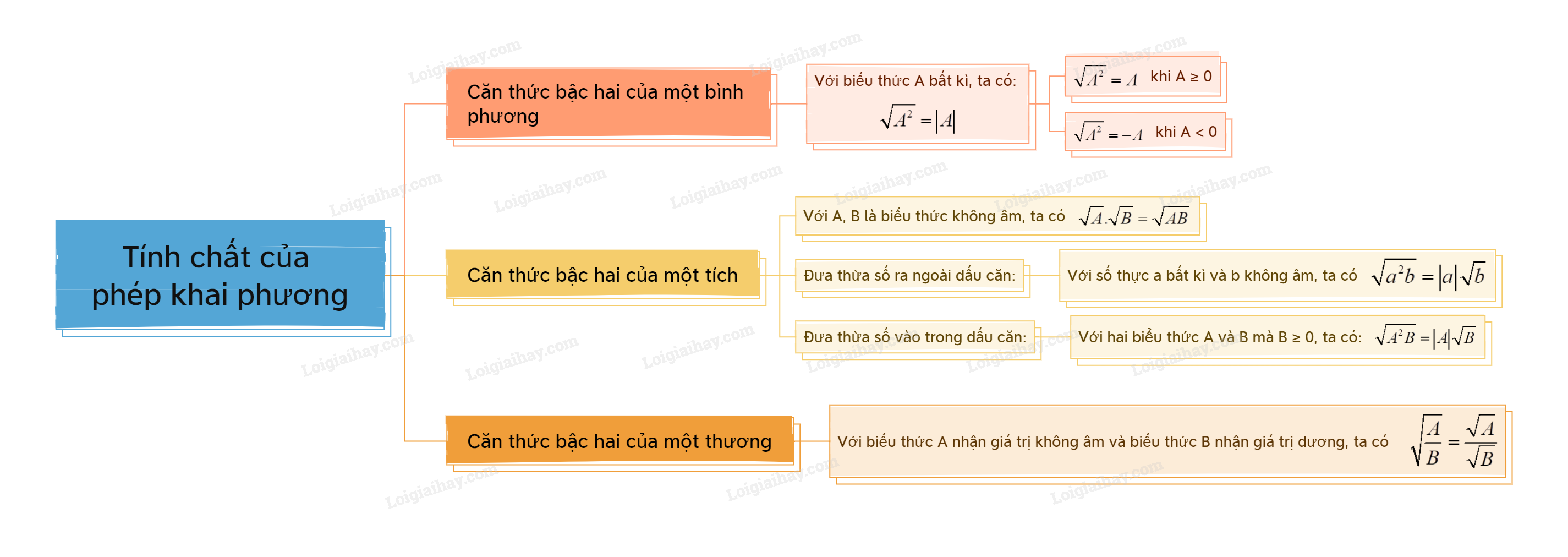
Sơ đồ tư duy Tính chất của phép khai phương