Với giải sách bài tập Toán 6 Bài 3: Phép cộng các số nguyên sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 3: Phép cộng các số nguyên

Bài 19 trang 76 sách bài tập Toán lớp 6 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai? Giải thích.

a) Tổng của một số nguyên âm và một số nguyên dương là một số nguyên âm.

b) Tổng của một số nguyên dương và một số nguyên âm là một số nguyên dương.

c) Hai số đối nhau có tổng bằng 0.

Lời giải:

Phát biểu a) là sai. Vì chẳng hạn ta có -2 là một số nguyên âm và 3 là một số nguyên dương thì tổng (-2) + 3 = 3 – 2 = 1 là một số nguyên dương.

Phát biểu b) là sai. Vì chẳng hạn ta có – 15 là một số nguyên âm và 10 là một số nguyên dường thì tổng (-15) + 10 = - (15 – 10) = -5 là một số nguyên âm.

Phát biểu c) là đúng. Vì tổng của hai số nguyên đối nhau có tổng bằng 0.

Bài 20 trang 76 sách bài tập Toán lớp 6 Tập 1: Trong giờ học nhóm, ba bạn An, Bình, Chi đã lần lượt phát biểu như sau:

a) Bạn An: “Tổng của hai số nguyên dương luôn lớn hơn mỗi số hạng của nó”.

b) Bạn Bình: “Tổng của hai số nguyên âm luôn lớn hơn mỗi số hạng của nó”.

c) Bạn Chi: “Tổng của hai số nguyên cùng dấu luôn cùng dấu với hai số nguyên đó”.

Bạn nào phát biểu đúng, bạn nào phát biểu sai? Giải thích.

Lời giải:

a) Bạn An phát biểu đúng vì nếu a và b là hai số nguyên dương thì a > 0, b > 0 nên tổng a + b > a, a + b > b.

b) Bạn Bình phát biểu sai. Chẳng hạn, ta có hai số nguyên âm là – 3 và – 12 thì tổng (- 3) + (- 12) = - (3 + 12) = - 15, mà – 15 < - 3, - 15 < - 12.

c) Bạn Chi phát biểu đúng vì nếu a và b cùng là hai số nguyên dương thì tổng a + b cũng là số nguyên dương, nếu a và b cùng là hai số nguyên âm thì tổng a + b cũng là số nguyên âm.

Bài 21 trang 76 sách bài tập Toán lớp 6 Tập 1: Một chiếc tàu ngầm đang ở độ cao – 25m so với mực nước biển, tàu tiếp tục lặn xuống thêm 10m nữa. Độ cao mới của tàu đó so với mực nước biển là bao nhiêu?

Lời giải:

Chiếc tàu ngầm đang ở độ sâu 25 m.

Sau khi lặn xuống thêm 10m thì tàu ngầm đang ở độ sâu: 25 + 10 = 35m.

Độ cao mới của tàu so với mực nước biển là: - 35m.

Vậy độ cao mới của tàu so với mực nước biển là -35m.

Bài 22 trang 76 sách bài tập Toán lớp 6 Tập 1: Nhiệt độ phòng đông lạnh của công ty cá Bình An đang là – 6⁰C. Bác Lan đã điều chỉnh nhiệt độ phòng đông lạnh hai lần. Lần một giảm nhiệt độ xuống bớt 7⁰C, lần hai lại tăng nhiệt độ thêm 5⁰C. Sau hai lần điều chỉnh, nhiệt độ trong phòng là bao nhiêu độ C.

Lời giải:

Sau lần điều chỉnh thứ nhất, nhiệt độ trong phòng là: - 6 – 7 = - (6 + 7) = -13⁰C.

Sau lần điều chỉnh thứ hai, nhiệt độ trong phòng là: - 13 + 5 = - (13 – 5) = - 8⁰C.

Vậy sau hai lần điều chỉnh, nhiệt độ trong phòng là – 8⁰C.

Bài 23 trang 76 sách bài tập Toán lớp 6 Tập 1: Một nhà hàng hải sản nợ ngân hàng 30 triệu đồng, sau đó nhà hàng đã phải trả nợ ngân hàng 10 triệu đồng. Số dư tài khoản của nhà hàng ở ngân hàng là bao nhiêu?

Lời giải:

Nhà hàng hải sản đang có – 30 (triệu đồng).

Sau khi trả nợ ngân hàng 10 triệu đồng thì nhà hàng đang có: - 30 + 10 = - (30 – 10) = -20 (triệu đồng).

Vậy số dư tài khoản của nhà hàng ở ngân hàng là: - 20 triệu đồng.

Bài 24 trang 76 sách bài tập Toán lớp 6 Tập 1: Chọn số thích hợp cho dấu :

Lời giải:

+) Với a = -13, b = 125, c = - 17 

a + b = (-13) + 125 = 125 – 3 = 112;

a + b + c = (-13) + 125 + (-17) = (125 – 13) + (-17) = 112 + (-17) = 112 – 17 = 95.

+) Với a = -199, b = -1 222, c = 199

a + b = (-199) + (-1 222) = - (199 + 1 222) = - 1 421;

a + b + c = (-199) + (-1 222) + 199 = [(-199) +199] + (-1 222) = 0 + (-1 222) = -1 222.

+) Với a = - 21, c = -17, a + b = -21

Ta có a + b = -21 

Suy ra b = (-21) – a = (-21) – (-21) = (-21) + 21 = 21 – 21 = 0;

Do đó a + b + c = (-21) + 0 + (-17) = (-21) + (-17) = -(21 + 17) = -38.

+) Với a = -398, b = 396, a + b + c = -988

a + b = (-398) + 396 = -(398 – 396) = -2;

Ta có: a + b + c = -988

c = (-988) – (a + b) 

c = (-988) – (-2) 

c = (-988) + 2

c = -(988 – 2) 

c = -986.

Khi đó ta có bảng sau: 

Bài 25 trang 77 sách bài tập Toán lớp 6 Tập 1:

a) Cho a là số nguyên dương nhỏ nhất có hai chữ số chia hết cho 2 và 5; b là số nguyên âm lớn nhất có ba chữ số. Tính tổng a + b.

b) Cho m là số nguyên dương nhỏ nhất có ba chữ số khác nhau; n là số nguyên dương nhỏ nhất có bốn chữ số và p là số nguyên âm nhỏ nhất có năm chữ số. Tính tổng m + n + p.

Lời giải:

a) Vì a chia hết cho 2 và 5 nên a có chữ số tận cùng là 0.

Hơn nữa a là số nguyên dương nhỏ nhất có hai chữ số nên a = 10.

Ta có b là số nguyên âm lớn nhất có ba chữ số nên b = -100.

Tổng a + b = 10 + (-100) = -(100 – 10) = -90.

Vậy a + b = -90.

b) Vì m là số nguyên dương nhỏ nhất có ba chữ số khác nhau nên m = 102.

Vì n là số nguyên dương nhỏ nhất có bốn chữ số nên n = 1 000.

Vì p là số nguyên âm nhỏ nhất có năm chữ số nên p = -99 999.

Tổng m + n + p = 102 + 1 000 + (-99 999) = 1 102 + (-99 999) = -(99 999 – 1 102) = -98 897.

Vậy m + n + p = - 98 897.

Bài 26 trang 77 sách bài tập Toán lớp 6 Tập 1: Thực hiện phép tính:

a) 145 + 43 + (-145) + 57;

b) (-123) + 101 + (-777) + 99;

c) (-8 955) + 33 + (-45) + (-133);

d) (-2) + (-4) + (-6) + (-8) + (-10) + 8 + 10 + 12;

e) (-2 020) + (-598) + (-201) + 498 + 301;

f) (-1) + (-2) + 3 + 4 + … + (-97) + (-98) + 99 + 100.

Lời giải:

a) 145 + 43 + (-145) + 57

= [145 + (-145)] + [43 + 57]

= 0 + 100

= 100;

b) (-123) + 101 + (-777) + 99

= [(-123) + (-777)] + (101 + 99)

= (-900) + 200

= -(900 – 200)

= -700;

c) (-8 955) + 33 + (-45) + (-133)

= [(-8 955) + (-45)] + [33 + (-133)]

= [-(8 955 + 45)] + [-(133 – 33)]

= (-9 000) + (-100)

= -(9 000 + 100)

= -9 100.

d) (-2) + (-4) + (-6) + (-8) + (-10) + 8 + 10 + 12

= (-6) + (-6) + [(-8) + 8] + [(-10) + 10] + 12

= (-12) + 0 + 0 + 12

= (-12) + 12

= 12 – 12

= 0;

e) (-2 020) + (-598) + (-201) + 498 + 301

= (-2 020) + [(-598) + 498] + [(-201) + 301]

= (-2 020) + [-(598 – 498)] + [301 – 201]

= (-2 020) + (-100) + 100

= (-2 020) + [(-100) + 100]

= (-2 020) + (100 – 100)

= (-2 020) + 0

= -2 020;

f) (-1) + (-2) + 3 + 4 + … + (-97) + (-98) + 99 + 100.

= [(-1) + 3 + (-5) + … + (-97) + 99] + [(-2) + 4 + (-6) + … + (-98) + 100]

Xét (-1) + 3 + (-5) + … + (-97) + 99

Số số hạng của tổng là: [99 – (-1)]:2 + 1 = 50.

Khi đó: (-1) + 3 + (-5) + … + (-97) + 99

= [(-1) + 3] + [(-5) + 7] + … + [(-97) + 99]

= 2 + 2 + … + 2

= 2.(50:2)

= 2.25

= 50.

Xét (-2) + 4 + (-6) + … + (-98) + 100

Số số hạng của tổng là: (100 – 2):2 + 1 = 50.

Khi đó: (-2) + 4 + (-6) + … + (-98) + 100

= [(-2) + 4] + [(-6) + 8] + … + [(-98) + 100]

= 2 + 2 + … + 2

= 2.(50:2)

= 2.25

= 50.

Suy ra: (-1) + (-2) + 3 + 4 + … + (-97) + (-98) + 99 + 100

= [(-1) + 3 + (-5) + … + (-97) + 99] + [(-2) + 4 + (-6) + … + (-98) + 100]

= 50 + 50

= 100.

Bài 27 trang 77 sách bài tập Toán lớp 6 Tập 1: Một tòa nhà có 20 tầng và 3 tầng hầm. Người ta biểu thị tầng G (tầng có mặt sàn là mặt đất) là 0, tầng hầm B1 là -1 và tầng hầm B2 là -2, … Hãy dùng phép cộng số nguyên để diễn tả tình huống sau: Một người đang ở tầng 2, người đó đi thang máy lên 8 tầng, sau đó lại đi xuống 11 tầng. Cuối cùng người đó dừng lại ở tầng thứ mấy?

Lời giải:

Số nguyên biểu thị cho tầng người đó đang ở là 2.

Người đó đi thang máy lên 8 tầng, sau đó lại đi xuống 11 tầng là: 2 + 8 - 11 = 10 – 11 = -(11 – 10) = - 1.

Người đó dừng lại ở tầng B1.

Bài 28 trang 77 sách bài tập Toán lớp 6 Tập 1: Cho 43 số nguyên, trong đó tổng của 7 số bất kì là một số nguyên âm. Chứng minh rằng tổng của 43 số đó là số nguyên âm.

Lời giải:

Trong 43 số nguyên ta có tổng của 7 số nguyên bất kì là một số nguyên âm nên trong đó có ít nhất một số nguyên âm. Gọi số nguyên âm này là a (a < 0). Còn lại 42 số nguyên nghĩa là có 6 tổng của 7 số nguyên âm bất kì mà tổng 7 số nguyên bất kì là một số nguyên âm nên 6 tổng này cũng là một số nguyên âm.

Vì vậy tổng của 43 số đó là số nguyên âm.

Bài 29 trang 77 sách bài tập Toán lớp 6 Tập 1: Bạn Nam xây dựng một tháp các số như sau:

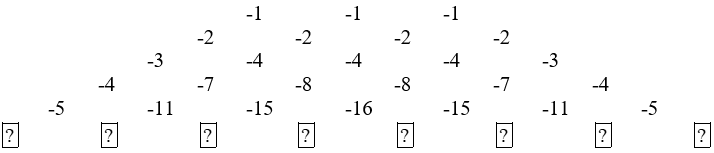
a) Hãy khám phá quy luật xây tháp của bạn Nam để tìm các số thích hợp cho .

b) Tính tổng tất cả các số vừa tìm được ở .

Lời giải:

a) Gọi hàng thứ nhất là hàn chứa dãy số: -1; -1; -1;

Hàng thứ hai là hàng chứa dãy số: -2; -2; -2; -2;

…

Hàng thứ sáu là hàng gồm 8 số cần tìm.

Ta thấy trong mỗi hàng không kể số đứng ở vị trị đầu bên trái của hàng và vị trí cuối bên phải của hàng, mỗi số khác trong hàng đều bằng tổng của hai số ở vị trí ngay phía trên thuộc hàng trước nó. 

Các số ở vị trí đầu hàng và vị trí cuối hàng theo quy luật như sau: -1; -2; -3; -4; -5;…

Vậy số cần tìm ở đầu hàng và cuối hàng của hàng thứ sáu là -6.

Các số cần tìm tiếp theo lần lượt từ trái sang phải là: -16; -26; -31; -31; -26; -16.

b) Tổng các số vừa tìm được: 

(-6) + (-16) + (-26) + (-31) + (-31) + (-26) + (-16) + (-6)

= [(-6) + (-6)] + [(-16) + (-16)] + [(-26) + (-26)] + [(-31) + (-31)]

= (-12) + (-32) + (-52) + (-62)

= (-44) + (-114)

= (-158).

Lý thuyết Phép cộng các số nguyên

I. Phép cộng hai số nguyên cùng dấu 

1. Phép cộng hai số nguyên dương 

Cộng hai số nguyên dương chính là cộng hai số tự nhiên khác 0. 

Ví dụ: 7 + 5 = 12

2. Phép cộng hai số nguyên âm

Để cộng hai số nguyên âm, ta làm như sau:

Bước 1. Bỏ đấu “–” trước mỗi số

Bước 2. Tính tổng của hai số nguyên dương nhận được ở Bước 1

Bước 3. Thêm dấu “–” trước kết quả nhận được ở Bước 2, ta có tổng cần tìm.

Ví dụ: (– 80) + (– 6) = – (80 + 6) = – 86

Chú ý: 

+ Tổng của hai số nguyên dương là số nguyên dương.

+ Tổng của hai số nguyên âm là số nguyên âm.

II. Phép cộng hai số nguyên khác dấu 

Để cộng hai số nguyên khác dấu, ta làm như sau:

Bước 1. Bỏ dấu “–” trước số nguyên âm, giữ nguyên số còn lại

Bước 2. Trong hai số nguyên dương nhận được ở Bước 1, ta lấy số lớn hơn trừ đi số nhỏ hơn

Bước 3. Cho hiệu vừa nhận được dấu ban đầu của số lớn hơn ở Bước 2, ta có tổng cần tìm.

Ví dụ: (– 6) + 3 = – (6 – 3) = – 3

Chú ý: Hai số nguyên đối nhau có tổng bằng 0.

Chẳng hạn, – 7 và 7 là hai số nguyên đối nhau, ta có: (– 7) + 7 = 0. 

III. Tính chất của phép cộng các số nguyên 

Phép cộng các số nguyên có các tính chất sau:

+ Giao hoán: a + b = b + a;

+ Kết hợp: (a + b) + c = a + ( b + c);

+ Cộng với số 0: a + 0 = 0 + a = a;

+ Cộng với số đối: a + (– a) = (– a) + a = 0.

Ví dụ: Tính: a) 51 + (– 97) + 49;                   b) 65 + (– 42) + (– 65).

Lời giải:

a) 51 + (– 97) + 49 

= 51 + 49 + (– 97)       (tính chất giao hoán)

= (51 + 49) + (– 97)    (tính chất kết hợp)

= 100 + (– 97) 

= 100 – 97 

= 3. 

b) 65 + (– 42) + (– 65) 

= 65 + (– 65) + (– 42)                         (tính chất giao hoán) 

= [65 + (– 65)] + (– 42)                      (tính chất kết hợp)

= 0 + (– 42)                                         (cộng với số đối)

= – 42.                                     (cộng với số 0)