Với giải bài tập Toán lớp 6 Bài 3: Phép cộng các số nguyên chi tiết bám sát nội dung sgk Toán 6 Tập 1 Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:

Giải bài tập Toán 6 Bài 3: Phép cộng các số nguyên

Video giải Toán 6 Bài 3: Phép cộng các số nguyên - Cánh diều

Trả lời câu hỏi giữa bài

Giải Toán 6 trang 70 Tập 1 Cánh diều

Câu hỏi khởi động trang 70 Toán lớp 6 Tập 1: Thống kê lợi nhuận hai tuần của một cửa hàng bán hoa quả như sau:

Sau hai tuần kinh doanh, cửa hàng lãi hay lỗ và với số tiền bao nhiêu?

Lời giải:

Để biết được cửa hàng kinh doanh lãi hay lỗ sau 2 tuần, ta tính tổng lợi nhuận của tuần I và tuần II. 

Ta thấy tuần I cửa hàng có lợi nhuận là – 2 triệu đồng, nghĩa là tuần I cửa hàng kinh doanh lỗ 2 triệu. Tuần II cửa hàng có lợi nhuận là 6 triệu đồng, vậy là cửa hàng kinh doanh lãi 6 triệu đồng. 

Khi đó ta lấy số tiền lời trừ đi số tiền lỗ ta được lợi nhuận của cả hai tuần là: 

6 – 2 = 4 (triệu đồng)

Như vậy, sau hai tuần kinh doanh, cửa hàng lãi với số tiền là 4 triệu đồng. 

Từ đó, ta biết được 4 chính là tổng của (–  2) và 6. 

Do đó, qua bài học này, chúng ta sẽ biết được cách thực hiện phép cộng hai số nguyên.

Hoạt động 1 trang 70 Toán lớp 6 Tập 1: Để phát triển tăng gia sản xuất, gia đình bạn Vinh đã vay Ngân hàng Chính sách xã hội 3 triệu đồng, sau đó lại vay thêm 5 triệu đồng nữa. Mẹ bạn Vinh đã viết vào sổ tay như hình bên dưới.

a) Tổng số tiền nợ ngân hàng của gia đình bạn Vinh là bao nhiêu?

b) Biểu thị “nợ 3” bởi số – 3, “nợ 5” bởi số – 5. Viết phép tính biểu thị tổng số tiền nợ ngân hàng của gia đình bạn Vinh bằng cách sử dụng số nguyên âm.

Lời giải:

a) Tổng số tiền nợ ngân hàng của gia đình bạn Vinh là: 

3 + 5 = 8 (triệu đồng)

b) Biểu thị "nợ 3" bởi số – 3, "nợ 5" bởi số – 5

Phép tính biểu thị tổng số tiền nợ ngân hàng của gia đình bạn Vinh là: (– 3) + (– 5) 

Giải Toán 6 trang 71 Tập 1 Cánh diều

Hoạt động 2 trang 71 Toán lớp 6 Tập 1:

Lời giải:

Để tính tổng hai số nguyên âm (– 3) + (– 5), ta làm như sau:

Bước 1. Bỏ dấu "–" trước mỗi số	– 3  3 – 5  5
Bước 2. Tính tổng của hai số nhận được ở Bước 1	3 + 5 = 8
Bước 3. Thêm đấu “–” trước tổng nhận được ở Bước 2.	8  – 8  Ta có: (– 3) + (– 5) = – (3 + 5) = – 8.

Minh hoa trên trục số ở Hình 7:  Từ điểm – 3 ta lùi sang trái 5 đơn vị đến điểm mới là – 8.

Luyện tập 1 trang 71 Toán lớp 6 Tập 1: Tính:

a) (– 28) + (– 82);

b) x + y, biết x = – 81, y = – 16.

Lời giải:

Ta có:

a) (– 28) + (– 82) = – (28 + 82) = –110.

b) Với x = – 81, y = – 16

Khi đó: x + y = (– 81) + (– 16) = – (81 + 16) = – 97.

Giải Toán 6 trang 72 Tập 1 Cánh diều

Hoạt động 3 trang 72 Toán lớp 6 Tập 1: Vào một ngày mùa đông ở Sa Pa, nhiệt độ tại Cổng Trời là – 1 °C. Tuy nhiên, nhiệt độ lúc đó tại chợ Sa Pa lại cao hơn 2 °C so với nhiệt độ tại Cổng Trời.

Viết phép tính và tính nhiệt độ tại chợ Sa Pa lúc đó. 

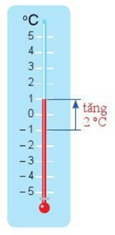
Lời giải:

Nhiệt độ tại chợ Sa Pa là (– 1) + 2 (^oC).

Quan sát nhiệt kế ta thấy nhiệt độ tại chợ Sa Pa là 1°C. Vậy (– 1) + 2 = 1 (^oC).

Hoạt động 4 trang 72 Toán lớp 6 Tập 1:

Lời giải:

Để tính tổng hai số nguyên khác dấu (– 1) + 2, ta làm như sau:

Bước 1. Bỏ dấu "–" trước số nguyên âm, giữ nguyên số còn lại	– 1  1 2  2
Bước 2. Trong hai số nguyên dương nhận được ở Bước 1, ta lấy số lớn hơn trừ đi số nhỏ hơn	Số lớn hơn: 2 Số nhỏ hơn: 1 2 – 1 = 1
Bước 3. Cho hiệu vừa nhận được dấu ban đầu của số lớn hơn ở Bước 2	1   1 Ta có: (– 1) + 2 = 2 – 1 = 1

Minh hoạ trên trục số ở Hình 8: Từ điểm – 1 ta tiến sang phải 2 đơn vị đến điểm mới là 1.

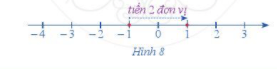
Giải Toán 6 trang 73 Tập 1 Cánh diều

Luyện tập 2 trang 73 Toán lớp 6 Tập 1: Tính:

a) (– 28) + 82;

b) 51 + (– 97).

Lời giải:

Ta có:

a) (– 28) + 82 = 82 – 28 = 54. 

b) 51 + (– 97) = – (97 – 51) = – 46.

Hoạt động 5 trang 73 Toán lớp 6 Tập 1: Tính và so sánh kết quả:

a) (– 25) + 19 và 19 + (– 25);

b) [(– 12) + 5] + (– 1) và (– 12) + [5 + (– 1)];

c) (– 18) + 0 và –18;

d) (– 12) + 12 và 0.

Lời giải:

a) (– 25) + 19 = – (25 – 19) = – 6

19 + (– 25) = – (25 – 19) = – 6

Vậy (– 25) + 19 = 19 + (–25). 

b) [(– 12) + 5] + (– 1) = [– (12 – 5)] + (– 1) = (– 7) + (– 1) = – (7 + 1) = – 8

(– 12) + [5 + (– 1)] = (– 12) + (5 – 1) = (– 12) + 4 = – (12 – 4) = – 8

Vậy [(– 12) + 5] + (– 1) = (– 12) + [5 + (– 1)]. 

c) (– 18) + 0 = – (18 – 0) = – 18

Vậy (– 18) + 0 = – 18. 

d) (– 12) + 12 = – (12 – 12) = – 0 = 0. 

Vậy (– 12) + 12 = 0.

Luyện tập 3 trang 73 Toán lớp 6 Tập 1: Tính một cách hợp lí:

a) 51 + (– 97) + 49;

b) 65 + (– 42) + (– 65).

Lời giải:

a) 51 + (– 97) + 49 

= 51 + 49 + (– 97)           (tính chất giao hoán)

= (51 + 49) + (– 97)         (tính chất kết hợp)

= 100 + (– 97) 

= 100 – 97 

= 3. 

b) 65 + (– 42) + (– 65) 

= 65 + (– 65) + (– 42)                (tính chất giao hoán) 

= [65 + (– 65)] + (– 42) 

= 0 + (– 42)                               (cộng với số đối)

= – 42.                   (cộng với số 0)

Bài tập

Giải Toán 6 trang 74 Tập 1 Cánh diều

Bài 1 trang 74 Toán lớp 6 Tập 1: Tính:

a) (– 48) + (– 67);

b) (– 79) + (– 45).

Lời giải:

a) (– 48) + (– 67) = – (48 + 67) = – 115. 

b) (– 79) + (– 45) = – (79 + 45) = – 124.

Bài 2 trang 74 Toán lớp 6 Tập 1: Trong các phát biểu sau đây, phát biểu nào đúng, phát biểu nào sai? Giải thích.

a) Tổng của hai số nguyên dương là số nguyên dương.

b) Tổng của hai số nguyên âm là số nguyên âm.

c) Tổng của hai số nguyên cùng dấu là số nguyên dương.

Lời giải:

a) Tổng của hai số nguyên dương là số nguyên dương là phát biểu đúng.

b) Tổng của hai số nguyên âm là số nguyên âm là phát biểu đúng.

c) Tổng của hai số nguyên cùng dấu là số nguyên dương là phát biểu sai vì tổng của hai số nguyên âm là số nguyên âm, không phải là số nguyên dương. 

Ví dụ: – 3 và – 7 là hai số nguyên âm nên nó là hai số nguyên cùng dấu

Tổng của – 3 và – 7 là (– 3) + (– 7) = – (3 + 7) = – 10 là một số nguyên âm, không phải là số nguyên dương.

Bài 3 trang 74 Toán lớp 6 Tập 1: Tính:

a) (– 2 018) + 2 018; 

b) 57 + (– 93); 

c) (– 38) + 46.

Lời giải:

a) (– 2 018) + 2018 = 0. (vì – 2 108 và 2 018 là hai số đối nhau)

b) 57 + (– 93) = (– 93) + 57 = – (93 – 57) = – 36. 

c) (– 38) + 46 = 46 + (– 38) = 46 – 38 = 8.

Bài 4 trang 74 Toán lớp 6 Tập 1: Cho ví dụ về phép cộng của hai số nguyên khác dấu sao cho:

a) Tổng của chúng là số nguyên dương;

b) Tổng của chúng là số nguyên âm.

Lời giải:

a) Để tổng của hai số nguyên khác dấu là số nguyên dương thì ta phải lấy hai số sao cho số nguyên âm sau khi bỏ đi dấu trừ phải nhỏ hơn số nguyên dương đã lấy ban đầu. Ta có thể đưa ra nhiều ví dụ thỏa mãn yêu cầu, chẳng hạn: 

+ Với – 5 và 10 là hai số nguyên khác dấu, ta có 

(–5) + 10 = 10 + (– 5) = 10 – 5 = 5 > 0

Do đó tổng của – 5 và 10 là 5 và nó là số nguyên dương. 

+ Với 21 và (– 13) là hai số nguyên khác dấu, ta có

21 + (– 13) = 21 – 13 = 8 > 0 

Do đó tổng của 21 và – 13 là 8 và nó là số nguyên dương. 

Tương tự, các em có thể chọn các ví dụ khác. 

b) Để tổng của hai số nguyên khác dấu là số nguyên âm thì ta phải lấy hai số sao cho số nguyên âm sau khi bỏ dấu trừ phải lớn hơn số nguyên dương đã lấy ban đầu. Ta có thể đưa ra nhiều ví dụ thỏa mãn yêu cầu, chẳng hạn:

+ Với – 30 và 20 là hai số nguyên khác dấu ta có

(– 30) + 20 = – (30 – 20) = – 10 < 0 

Do đó tổng của – 30 và 20 là – 10 và là số nguyên âm.

+ Với – 48 và 22 là hai số nguyên khác dấu ta có

(– 48) + 22 = – (48 – 22) = – 26 < 0 

Do đó tổng của – 48 và 22 là – 26 và là số nguyên âm.  

Tương tự, các em có thể chọn nhiều ví dụ khác.

Bài 5 trang 74 Toán lớp 6 Tập 1: Tính một cách hợp lí:

a) 48 + (– 66) + (– 34); 

b) 2 896 + (–2 021) + (– 2 896).

Lời giải:

a) 48 + (– 66) + (– 34) 

= 48 + [(– 66) + (– 34)]             (tính chất kết hợp)

= 48 + [– (66 + 34)]

= 48 + (– 100) 

= – (100 – 48) 

= – 52. 

b) 2 896 + (– 2 021) + (– 2 896) 

= 2 896 + (– 2 896) + (– 2 021)           (tính chất giao hoán)

= [2 896 + (– 2 896)] + (– 2 021)         

= 0 + (– 2 021)                                     (cộng hai số đối nhau) 

= – 2 021.                                            (cộng với 0)

Bài 6 trang 74 Toán lớp 6 Tập 1: Nhiệt độ ở Thủ đô Ôt-ta-oa, Ca-na-đa (Ottawa, Canada) lúc 7 giờ là – 4 °C, đến 10 giờ 6 °C. Nhiệt độ ở Ôt-ta-oa lúc 10 giờ là bao nhiêu?

Lời giải:

Lúc 7 giờ nhiệt độ ở thủ đô Ôt-ta-oa là – 4 °C, đến 10 giờ tăng thêm 6 °C

Do đó nhiệt độ ở Ôt-ta-oa lúc 10 giờ là: 

(– 4) + 6 = 2 (°C)

Vậy nhiệt độ ở Ôt-ta-oa lúc 10 giờ là 2 °C.

Bài 7 trang 74 Toán lớp 6 Tập 1: Một cửa hàng kinh doanh có lợi nhuận như sau: tháng đầu tiên là – 10 000 000 đồng; tháng thứ hai là 30 000 000 đồng. Tính lợi nhuận của cửa hàng sau hai tháng đó.

Lời giải:

Lợi nhuận tháng đầu tiên của cửa hàng là – 10 000 000 đồng

Lợi nhuận tháng thứ hai của cửa hàng là 30 000 000 đồng

Do đó lợi nhuận của cửa hàng sau hai tháng đó là: 

(– 10 000 000) + 30 000 000 = 20 000 000 (đồng)

Vậy lợi nhuận của cửa hàng sau hai tháng là 20 000 000 đồng.

Giải Toán 6 trang 75 Tập 1 Cánh diều

Bài 8 trang 75 Toán lớp 6 Tập 1: Để di chuyển giữa các tầng của toà nhà cao tầng, người ta thường sử dụng thang máy. Tầng có mặt sàn là mặt đất thường được gọi là tầng G, các tầng ở dưới mặt đất lần lượt từ trên xuống được gọi là B1, B2,... Người ta biểu thị vị trí tầng G là 0, tầng hầm B1 là – 1, tầng hầm B2 là – 2,...

a) Từ tầng G bác Sơn đi thang máy xuống tầng hầm B1. Sau đó bác đi xuống tiếp 2 tầng nữa. Tìm số nguyên biểu thị vị trí tầng mà bác Sơn đến khi kết thúc hành trình.

b) Bác Dư đang ở tầng hầm B2, sau đó bác đi thang máy lên 3 tầng rồi đi xuống

2 tầng. Tìm số nguyên biểu thị vị trí tầng mà bác Dư đến khi kết thúc hành trình.

Lời giải:

a) Số nguyên biểu thị vị trí tầng G là 0

Số nguyên biểu thị tầng B1 là – 1

Bác Sơn từ tầng B1 đi xuống 2 tầng nữa, có nghĩa là số tầng bác đi được biểu thị là – 2. 

Vậy số nguyên biểu thị vị trí tầng mà bác Sơn đến khi kết thúc hành trình là

 0 + (– 1) + (– 2) = – 3. 

b) Bác Dư đang ở tầng hầm B2, số nguyên biểu thị tầng hầm B2 là – 2

Sau đó bác đi thang máy lên 3 tầng, có nghĩa là số tầng bác đi lần này được biểu thị là 3 (hoặc + 3)

Tiếp theo bác đi xuống 2 tầng, có nghĩa là số tầng bác đi lúc này được biểu thị là – 2. 

Vậy số nguyên biểu thị vị trí tầng mà bác Dư kết thúc hành trình là: 

(– 2) + 3 + (–2) = – 1.

Bài 9 trang 75 Toán lớp 6 Tập 1: Mỗi người khi ăn thì sẽ hấp thụ ca-lo và khi hoạt động thì sẽ tiêu hao ca-lo. Bạn Bình dùng phép cộng số nguyên để tính số ca-lo hàng ngày của mình bằng cách xem số ca-lo hấp thụ là số nguyên dương và số tiêu hao là số nguyên âm. Em hãy giúp bạn Bình kiếm tra tổng số ca-lo còn lại sau khi ăn sáng và thực hiện các hoạt động (theo số liệu trong Hình 9).

Lời giải:

Tổng số ca-lo còn lại sau khi ăn sáng và thực hiện các hoạt động của bạn Bình là

290 + 189 + 110 + (– 70) + (– 130) (ca-lo)

Ta tính tổng:

290 + 189 + 110 + (– 70) + (– 130) 

= (290 + 110) + [(– 70) + (– 130)] + 189       (tính chất giao hoán và kết hợp)

= 400 + [– (70 + 130)] + 189 

= 400 + (– 200) + 189 

= 400 – 200 + 189 

= 200 + 189 = 389. 

Vậy tổng số ca-lo còn lại sau khi ăn sáng và thực hiện các hoạt động của bạn Bình là 389 ca-lo.

Bài 10 trang 75 Toán lớp 6 Tập 1: Sử dụng máy tính cầm tay

Nút dấu âm: 

Chú ý: Ở một số máy tính cầm tay, nút dấu âm có dạng  .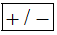

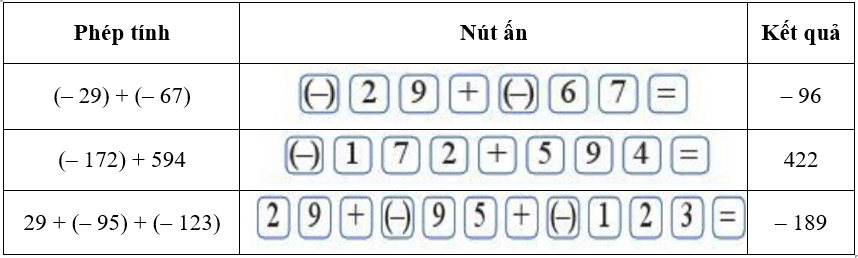
Dùng máy tính cầm tay để tính:

(– 123) + (– 18); 

(– 375) + 210; 

(– 127) + 25 + (– 136).

Lời giải:

Sử dụng máy tính bỏ túi, ta tính được:

(– 123) + (– 18) = – 141;

(– 375) + 210 = – 165;

(– 127) + 25 + (– 136) = – 238.

Lý thuyết Phép cộng các số nguyên

I. Phép cộng hai số nguyên cùng dấu 

1. Phép cộng hai số nguyên dương 

Cộng hai số nguyên dương chính là cộng hai số tự nhiên khác 0. 

Ví dụ: 7 + 5 = 12

2. Phép cộng hai số nguyên âm

Để cộng hai số nguyên âm, ta làm như sau:

Bước 1. Bỏ đấu “–” trước mỗi số

Bước 2. Tính tổng của hai số nguyên dương nhận được ở Bước 1

Bước 3. Thêm dấu “–” trước kết quả nhận được ở Bước 2, ta có tổng cần tìm.

Ví dụ: (– 80) + (– 6) = – (80 + 6) = – 86

Chú ý: 

+ Tổng của hai số nguyên dương là số nguyên dương.

+ Tổng của hai số nguyên âm là số nguyên âm.

II. Phép cộng hai số nguyên khác dấu 

Để cộng hai số nguyên khác dấu, ta làm như sau:

Bước 1. Bỏ dấu “–” trước số nguyên âm, giữ nguyên số còn lại

Bước 2. Trong hai số nguyên dương nhận được ở Bước 1, ta lấy số lớn hơn trừ đi số nhỏ hơn

Bước 3. Cho hiệu vừa nhận được dấu ban đầu của số lớn hơn ở Bước 2, ta có tổng cần tìm.

Ví dụ: (– 6) + 3 = – (6 – 3) = – 3

Chú ý: Hai số nguyên đối nhau có tổng bằng 0.

Chẳng hạn, – 7 và 7 là hai số nguyên đối nhau, ta có: (– 7) + 7 = 0. 

III. Tính chất của phép cộng các số nguyên 

Phép cộng các số nguyên có các tính chất sau:

+ Giao hoán: a + b = b + a;

+ Kết hợp: (a + b) + c = a + ( b + c);

+ Cộng với số 0: a + 0 = 0 + a = a;

+ Cộng với số đối: a + (– a) = (– a) + a = 0.

Ví dụ: Tính: a) 51 + (– 97) + 49;                   b) 65 + (– 42) + (– 65).

Lời giải:

a) 51 + (– 97) + 49 

= 51 + 49 + (– 97)       (tính chất giao hoán)

= (51 + 49) + (– 97)    (tính chất kết hợp)

= 100 + (– 97) 

= 100 – 97 

= 3. 

b) 65 + (– 42) + (– 65) 

= 65 + (– 65) + (– 42)                         (tính chất giao hoán) 

= [65 + (– 65)] + (– 42)                      (tính chất kết hợp)

= 0 + (– 42)                                         (cộng với số đối)

= – 42.                                     (cộng với số 0)