Với giải sách bài tập Toán 6 Bài 13: Bội chung và bội chung nhỏ nhất sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 13: Bội chung và bội chung nhỏ nhất

Bài 119 trang 36 sách bài tập Toán lớp 6 Tập 1: Tìm bội chung nhỏ nhất của:

a) 19 và 46;

b) 27 và 315;

c) 60, 72 và 63;

d) 60, 100 và 140

Lời giải:

a) Ta có: 19 = 19, 46 = 2.23.

Tích các thừa số chung và riêng với số mũ lớn nhất là: 2.19.23.

Vậy BCNN(19, 46) = 2.19.23 = 874.

b) Ta có: 27 = 3³, 315 = 3².5.7.

Tích các thừa số chung và riêng với số mũ lớn nhất là: 33.5.7.

Vậy BCNN(27, 315) = 3³.5.7 = 945.

c) Ta có: 60 = 2².3.5, 72 = 2³.3², 63 = 3².7.

Tích các thừa số chung và riêng với số mũ lớn nhất là: 23.32.5.7.

Vậy BCNN(60, 72, 63) = 2³.3².5.7 = 2 520.

d) Ta có: 60 = 2².3.5, 100 = 2².5², 140 = 2².5.7.

Tích các thừa số chung và riêng với số mũ lớn nhất là: 2².3.5².7.

BCNN(60, 100, 140) = 22.3.52.7 = 2 100.

Bài 120 trang 36 sách bài tập Toán lớp 6 Tập 1: Có bao nhiêu số tự nhiên có ba chữ số là bội chung của 11 và 12?

Lời giải:

Ta có: 11 = 11, 12 = 2².3.

BCNN(11, 12) = 2².3.11 = 132.

BC(132) = {0; 132; 264; 396; 528; 660; 792; 924; 1 056; …}.

Các số tự nhiên có ba chữ số là bội chung của 11 và 12 là: 132; 264; 396; 528; 660; 792; 924.

Vậy có tất cả 7 số tự nhiên có ba chữ số là bội chung của 11 và 12.

Bài 121 trang 36 sách bài tập Toán lớp 6 Tập 1: Lịch cập cảng của ba tàu như sau: tàu thứ nhất cứ 5 ngày cập cảng một lần; tàu thứ hai cứ 8 ngày cập cảng một lần; tàu thứ ba cứ 10 ngày cập cảng một lần. Vào một ngày nào đó, ba tàu cùng cập cảng. Sau ít nhất bao nhiêu ngày thì ba tàu lại cùng cập cảng?

Lời giải:

Chu kì số ngày cả ba tàu cùng cập cảng là bội chung của 5, 8 và 10.

Mà cần tìm sau ít nhất bao nhiêu ngày thì ba tàu lại cùng cập cảng nên số ngày gặp nhau là BCNN(5, 8, 10).

Ta có 5 = 5, 8 = 2³, 10 = 2².5.

BCNN(5, 8, 10) = 2³.5 = 40.

Vậy vào một ngày nào đó, ba tàu cùng cập cảng thì sau ít nhất 40 ngày thì ba tàu sẽ lại cùng cập cảng.

Bài 122 trang 36 sách bài tập Toán lớp 6 Tập 1: Trong một đợt trồng cây, học sinh của lớp 6B đã trồng được một số cây. Số đó là số tự nhiên nhỏ nhất thỏa mãn chia 3 dư 2, chia 4 dư 3, chia 5 dư 4, chia 10 dư 9. Học sinh lớp 6B đã trồng được bao nhiêu cây?

Lời giải:

Gọi số cây của lớp 6B đã trồng được là x (cây) ( x là số tự nhiên nhỏ nhất).

Theo đầu bài, ta có:

x chia 3 dư 2 nên x – 2 chia hết cho 3. Do đó x – 2 + 3 = x + 1 cũng chia hết cho 3;

x chia 4 dư 3 nên x – 3 chia hết cho 4. Do đó x – 3 + 4 = x + 1 cũng chia hết cho 4;

x chia 5 dư 4 nên x – 4 chia hết cho 5. Do đó x – 4 + 5 = x + 1 cũng chia hết cho 5;

x chia 10 dư 9 nên x – 9 chia hết cho 10. Do đó x – 9 + 10 = x + 1 cũng chia hết cho 10.

Suy ra x + 1 là bội chung của 3, 4, 5 và 10.

Mà x nhỏ nhất nên x + 1 nhỏ nhất nên x + 1 là bội chung nhỏ nhất của 3, 4, 5 và 10.

Ta có 3 = 3, 4 = 2², 5 = 5, 10 = 2.5.

Khi đó BCNN(3, 4, 5, 10) = 3.2².5 = 60.

Do đó x + 1 = 60. Suy ra x = 60 – 1 = 59 (thỏa mãn).

Vậy học sinh lớp 6B đã trồng được 59 cây.

Bài 123 trang 36 sách bài tập Toán lớp 6 Tập 1: Học sinh của một trường trung học cơ sở khi xếp hàng 20 học sinh, hàng 25 học sinh, hàng 30 học sinh đều thừa 15 học sinh, nhưng xếp vào hàng 41 học sinh thì vừa đủ. Tính số học sinh của trường đó, biết số học sinh của trường ít hơn 1 200 học sinh.

Lời giải:

Gọi số học sinh của trường đó là x (học sinh) (x ∈ N, x < 1200) .

Vì học sinh của trường đó khi xếp hàng 20 học sinh, hàng 25 học sinh, hàng 30 học sinh đều thừa 15 học sinh nên số học sinh của trường đó trừ đi 15 chia hết cho 20, 25, 30. Nghĩa là x – 15 thuộc BC(20, 25, 30).

Ta có 20 = 2².5, 25 = 5², 30 = 2.3.5.

Khi đó BCNN(20, 25, 30) = 2².3.5² = 300.

BC(20, 25, 30) = B(300) = {0; 300; 600; 900; 1 200; 1 500; …}.

Suy ra x – 15 ∈ {0; 300; 600; 900; 1 200; 1 500; …}.

Hay x ∈ {15; 315; 615; 915; 1 215; 1 515; …}.

Mà số học sinh xếp vào hàng 41 học sinh thì vừa đủ nên x chia hết cho 41.

Trong các giá trị của x ở trên ta thấy x = 615 chia hết cho 41 và nhỏ hơn 1 200.

Vậy trường đó có tất cả 615 học sinh.

Bài 124 trang 36 sách bài tập Toán lớp 6 Tập 1: Tìm số tự nhiên nhỏ nhất sao cho số đó chia cho 3 dư 1, chia cho 4 dư 3, chia cho 5 dư 1.

Lời giải:

Gọi số tự nhiên cần tìm là x (x > 1).

Vì x chia cho 3 dư 1, chia cho 5 dư 1 nên x – 1 chia hết cho 3 và 5.

Mà x chia cho 4 dư 3 nên x có dạng 4a + 3 với a là số tự nhiên.

Suy ra x – 1 = 4a + 3 – 1 = 4a + 2 chia hết cho 3 và 5.

Hơn nữa 4a + 2 = 2.(2a + 1) chia hết cho 2.

Do đó x – 1 chia hết cho 2, 3 và 5 hay x – 1 là bội chung của 2, 3 và 5.

Mà x là số tự nhiên nhỏ nhất nên x – 1 cũng nhỏ nhất. Do đó x – 1 là BCNN(2, 3, 5).

Ta có 2 = 2, 3 = 3, 5 = 5.

Khi đó BCNN(2, 3, 5) = 2.3.5 = 30.

x – 1 = 30

x = 31.

Vậy x = 31.

Bài 125 trang 37 sách bài tập Toán lớp 6 Tập 1: Tìm số tự nhiên nhỏ nhất sao cho số đó chia cho 3 dư 2, chia cho 5 dư 3, chia cho 7 dư 4.

Lời giải:

Gọi số tự nhiên cần tìm là a (a > 1).

Do a chia cho 3 dư 2, chia cho 5 dư 3, chia cho 7 dư 4 nên 2a chia cho 3, 5, 7 dư 1.

Suy ra 2a – 1 chia hết cho 3, 5, 7 hay 2a – 1 là bội chung của 3, 5, 7.

Như vậy để a là số tự nhiên nhỏ nhất thỏa mãn yêu cầu đề bài thì 2a – 1 phải là BCNN(3, 5, 7).

Ta có 3 = 3, 5 = 5, 7 = 7.

Khi đó BCNN(3, 5, 7) = 3.5.7 = 105 nên 2a – 1 = 105 suy ra a = 53.

Vậy số cần tìm là 53.

Bài 126 trang 37 sách bài tập Toán lớp 6 Tập 1: Tìm số tự nhiên có dạng  sao cho số đó chia hết cho 6, 7, 11 và 27.

Lời giải:

Số tự nhiên cần tìm chia hết cho 6, 7, 11 và 27 nên số đó là bội chung của 6, 7, 11 và 27.

Ta có: 6 = 2.3, 7 = 7, 11 = 11, 27 = 3³.

Khi đó BCNN(6, 7, 11, 27) = 2.3³.11.27 = 4 158.

Do đó 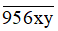 là bội của 4 158 hay tồn tại số tự nhiên k để  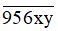= 4 158k.

Mặt khác 95 600 ≤ 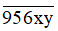 ≤ 95 699 nên 95 600  4 158k  95 699 hay 22 < k < 24.

Suy ra k = 23.

Ta có 4 158.23 = 95 634.

Do đó x = 3, y = 4.

Vậy số tự nhiên cần tìm là 95 634.

Bài 127 trang 37 sách bài tập Toán lớp 6 Tập 1: Tìm hai số tự nhiên a, b sao cho: 0 < a < b, a + b = 42 và BCNN(a, b) = 72

Lời giải:

Ta thấy BCNN(a, b) = 72 chia hết cho 2 nên trong hai số a, b có ít nhất một số chia hết cho 2.

Giả sử a chia hết cho 2, mà a + b = 42 chia hết cho 2 nên b chia hết cho 2. Như vậy, a và b đều chia hết cho 2.

Ta thấy BCNN(a, b) = 72 chia hết cho 3 nên trong hai số a, b có ít nhất một số chia hết cho 3.

Giả sử a chia hết cho 3, mà a + b = 42 chia hết cho 3 nên b chia hết cho 3. Như vậy, a và b đều chia hết cho 3.

Vì a, b vừa chia hết cho 2 vừa chia hết cho 3 nên a, b đều chia hết cho 6 hay a, b là bội của 6.

Mặt khác 0 < a < b, a + b = 42 và BCNN(a, b) = 72 nên có bảng giá trị sau: 

Vậy a = 18 và b = 24.

Lý thuyết Bội chung và bội chung nhỏ nhất

I. Bội chung và bội chung nhỏ nhất

1. Bội chung: Số tự nhiên n được gọi là bội chung của hai số a và b nếu n vừa là bội của a vừa là bội của b.

Quy ước: Viết tắt bội chung là BC. 

Kí hiệu: Tập hợp các bội chung của a và b là BC(a, b). 

Ví dụ: Các bội của 2 là: 0, 2, 4, 6, 8, 10, 12,…

Các bội của 3 là: 0, 3, 6, 9, 12,…

Các bội chung của 2 và 3 là: 0, 6, 12, … 

Vậy BC(2, 3) = {0; 6; 12; …} . 

Chú ý: Số tự nhiên n được gọi là bội chung của ba số a, b, c nếu n là bội của cả ba số a, b, c. Ta kí hiệu: Tập hợp các bội chung của a, b, c là BC(a, b, c).

Ví dụ: 20 chia hết cho 2 nên 20 là bội của 2, 20 chia hết cho 4 nên 20 là bội của 4, 20 chia hết cho 5 nên 20 là bội của 5. Do đó 20 là một bội chung của ba số 2, 4, 5. 

2. Bội chung nhỏ nhất: Số nhỏ nhất khác 0 trong các bội chung của a và b được gọi là bội chung nhỏ nhất của a và b.

Quy ước: Viết tắt bội chung nhỏ nhất là BCNN.

Kí hiệu: bội chung nhỏ nhất của a và b là BCNN(a, b).

Ví dụ: Ta có các bội chung của 2 và 3 là: 0, 6, 12,… Số nhỏ nhất khác 0 trong các bội chung của 2 và 3 là 6 nên 6 là bội chung nhỏ nhất của 2 và 3. 

Vậy BCNN(2, 3) = 6. 

Chú ý: 

+ Số nhỏ nhất khác 0 trong các bội chung của ba số a, b, c được gọi là bội chung nhỏ nhất của ba số a, b, c.

+ Kí hiệu: bội chung nhỏ nhất của a, b, c là BCNN(a, b, c).

+ Bội chung nhỏ nhất của hai số nguyên tố cùng nhau bằng tích của hai số đó. 

Ví dụ: 5 và 8 là hai số nguyên tố cùng nhau nên BCNN(5, 8) = 5 . 8 = 40. 

3. Tìm bội chung thông qua BCNN

+ Bội chung của nhiều số là bội của bội chung nhỏ nhất của chúng.

+ Để tìm bội chung của nhiều số, ta có thể lấy bội chung nhỏ nhất của chúng lần lượt nhân với 0, 1, 2, …

Ví dụ: Biết BCNN(a, b) = 30. Tìm tất cả các số có hai chữ số là bội chung của a và b.

Lời giải:

Vì bội chung của a và b đều là bội của BCNN(a, b) = 30 nên tất cả các số có hai chữ số là bội chung của a và b là: 30, 60, 90.

II. Tìm bội chung nhỏ nhất bằng cách phân tích các số ra thừa số nguyên tố 

Các bước tìm BCNN bằng cách phân tích các số ra thừa số nguyên tố

Bước 1: Phân tích mỗi số ra thừa số nguyên tố

Bước 2: Chọn ra các thừa số nguyên tố chung và các thừa số nguyên tố riêng

Bước 3: Với mỗi thừa số nguyên tố chung và riêng, ta chọn lũy thừa với số mũ lớn nhất

Bước 4: Lấy tích của các lũy thừa đã chọn, ta nhận được bội chung nhỏ nhất cần tìm.

Ví dụ: Tìm BCNN(40, 48).

Lời giải:

Ta có: 40 = 2³ . 5; 48 = 2⁴ . 3

Chọn ra các thừa số nguyên tố chung và riêng của 40 và 48, đó là 2, 3, 5.

Số mũ lớn nhất của 2 là 4; Số mũ lớn nhất của 3 là 1; Số mũ lớn nhất của 5 là 1.

Vậy BCNN(40, 48) = 2⁴  . 3 . 5 = 240.

Chú ý: Nếu   thì BCNN(a, b) = a. Chẳng hạn: BCNN(48, 16) = 48.

III. Ứng dụng bội cung nhỏ nhất vào cộng, trừ các phân số không cùng mẫu

Để tính tổng (hoặc hiệu) hai hay nhiều phân số không cùng mẫu, ta có thể làm như sau:

+ Quy đồng mẫu số hai phân số bằng cách chọn mẫu chung là BCNN của các mẫu. 

+ Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu).

+ Sau khi nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng, ta cộng (trừ) hai hay nhiều phân số có cùng mẫu. 

Ví dụ: Thực hiện phép tính:

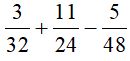
Lời giải:

BCNN(32, 24, 48) = 96

96 : 32 = 3; 96 : 24 = 4; 96 : 48 = 2