Với giải sách bài tập Toán 6 Bài 11: Phân tích một số ra thừa số nguyên tố sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:
Giải SBT Toán lớp 6 Bài 11: Phân tích một số ra thừa số nguyên tố
Lời giải:
+) Ta có:
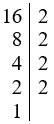
Vậy 16 = 24.
+) Ta có:
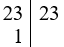
Vậy 23 = 23.
+) Ta có:
Vậy 120 = 23.3.5.
+) Ta có:
Vậy 625 = 54.
a) 777:7 + 361:192;
b) 3.52 – 3.17 + 43.7.
Lời giải:
a) 777:7 + 361:192
= 777:7 + 361:361
= 111 + 1
= 112.
Ta có:
Vậy 112 = 24.7.
b) 3.52 – 3.17 + 43.7
= 3.25 – 3.17 + 64.7
= 75 – 51 + 448
= 472
Ta có:
Vậy 472 = 23.59.
Lời giải:
Ta có:
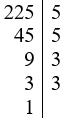
Vậy 225 = 32.52.
Suy ra 225 chia hết cho các số nguyên tố là 3 và 5.
Ta có:
Vậy 1 200 = 24.3.52.
Suy ra 1 200 chia hết cho các số nguyên tố là 2, 3 và 5.
Lời giải:
Cách 1. Ta có a = p.q2 nên tập các Ư(a) = {1; p; q; q2; pq; pq2}. Do đó a có 6 ước là đúng.
Cách 2. Nếu a = pm.qn thì số ước của a là: (m + 1).(n + 1).
Áp dụng vào bài toán, ta có a = p.q2 khi đó a có (1 + 1)(2 + 1) = 2.3 = 6. Vậy a có tất cả 6 ước là đúng.
Lời giải:
Ta có: 7a = 7. 72.113 = 73.113.
Suy ra 7a có tất cả (3 + 1).(3 + 1) = 4.4 = 16 ước.
Ta có: 11a = 11.72.113 = 72.114.
Suy ra 11a có tất cả (2 + 1).(4 + 1) = 3.5 = 16 ước.
Ta có: 13a = 13.72.113.
Suy ra 13a có tất cả (2 + 1).(3 + 1).(1 + 1) = 3.4.2 = 24 ước.
Vậy số 13a là số nhiều ước nhất.
Bài 104 trang 31 sách bài tập Toán lớp 6 Tập 1: Tìm số tự nhiên n, biết:
a) 2 + 4 + 6 + … + 2.(n – 1) + 2n = 210.
b) 1 + 3 + 5 + … + (2n – 3) + (2n – 1) = 225.
Lời giải:
a) Số số hạng của VT là: (2n – 2):2 + 1 = n – 1 + 1 = n số.
Khi đó: 2 + 4 + 6 + … + 2.(n – 1) + 2n = (2n + 2).n:2 = n.(n+1).
Theo đầu bài, ta có: n(n + 1) = 210
Ta có:
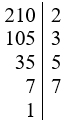
Suy ra 210 = 2.3.4.5= 14.15.
Vậy n = 14.
b) Số số hạng của VT là: (2n – 1 – 1):2 + 1 = (2n – 2):2 + 1 = n – 1 + 1 = n.
Khi đó 1 + 3 + 5 + … + (2n – 3) + (2n – 1) = (2n – 1 + 1).n:2 = 2n.n:2 = n2.
Ta có 223 = 32.52 = 152.
Vậy n = 15.
Lời giải:
Vì để xếp 16 cái bút vào các hộp sao cho số bút của các hộp bằng nhau nên số hộp bút là ước của 16.
Ta có: 16 = 24 nên các ước của 16 là: 1; 2; 4; 8; 16.
Ta có bảng sau:
|
Số hộp bút |
Số bút trong mỗi hộp |
|
1 |
16 |
|
2 |
8 |
|
4 |
4 |
|
8 |
2 |
|
16 |
1 |
Vì mỗi hộp có ít nhất hai cái bút nên ta loại trường hợp chia thành 16 hộp bút.
Vậy bạn Khanh có thể xếp số bút đó vào 1 hộp, 2 hộp, 4 hộp hoặc 8 hộp.
Lời giải:
Xếp 1 015 học sinh thành các hàng sao cho số học sinh mỗi hàng là như nhau nên số hàng là ước của 1 015.
Ta có: 1 015 = 5.7.29.
Ta có bảng sau:
|
Số hàng |
Số học sinh mỗi hàng |
|
1 |
1 015 |
|
5 |
203 |
|
7 |
145 |
|
29 |
35 |
|
35 |
29 |
|
145 |
7 |
|
203 |
5 |
|
1 015 |
1 |
Vì số hàng không quá 40 hàng và không ít hơn 10 hàng nên ta có thể xếp 1 015 thành
29 hàng hoặc 35 hàng.
Lời giải:
Vì mỗi học sinh đều nhận được phần thưởng là như nhau nên số học sinh vừa là ước của 215 vừa là ước của 129.
Ta có: 215 = 5.43; 129 = 3.43.
Do đó 43 vừa là ước của 215 vừa là ước của 129 và thỏa mãn lớn hơn 10 nên số học sinh của lớp 6A là 43 học sinh.
Bài 108 trang 32 sách bài tập Toán lớp 6 Tập 1: Tìm số tự nhiên n sao cho:
a) 3n + 13 chia hết cho n + 1;
b) 5n + 19 chia hết cho 2n + 1.
Lời giải:
a) Ta có: 3n + 13 = 3n + 3 + 10 = 3.(n + 1) + 10.
Vì 3.(n + 1) chia hết cho n + 1 nên để 3n + 13 chia hết cho n + 1 thì 10 phải chia hết cho n + 1 hay n + 1 là ước của 10.
Ta có: 10 = 2.5 nên các ước của 10 là: Ư(10) = {1; 2; 5; 10}.
Ta có bảng sau:
|
n + 1 |
1 |
2 |
5 |
10 |
|
n |
0 |
1 |
4 |
9 |
Vậy n ∈ {0; 1; 4; 9}.
b) 5n + 19 chia hết cho 2n + 1.
Vì 5n + 19 chia hết cho 2n + 1 nên 2(5n + 19) chia hết cho 2n + 1
Xét 2(5n + 19) = 10n + 38 = 10n + 5 + 33 = 5(2n + 1) + 33.
Vì 5.(2n + 1) chia hết cho 2n + 1 nên để 2(5n + 19) chia hết cho 2n + 1 thì 33 phải chia hết cho 2n + 1 hay 2n + 1 thuộc ước của 33.
Ta có bảng sau:
|
2n + 1 |
1 |
3 |
11 |
33 |
|
n |
0 |
1 |
5 |
16 |
Vậy n ∈ {0; 1; 5; 16}.
Lý thuyết Phân tích một số ra thừa số nguyên tố
I. Cách tìm một ước nguyên tố của một số
Để tìm một ước nguyên tố của số tự nhiên n lớn hơn 1, ta có thể làm như sau: lần lượt thực hiện phép chia n cho các số nguyên tố theo thứ tự tăng dần 2, 3, 5, 7, 11, 13, …
Khi đó, phép chia hết đầu tiên cho ta số chia là một ước nguyên tố của n.
Ví dụ: Tìm một ước nguyên tố của 217.
Lời giải:
Theo dấu hiệu chia hết, số 217 không chia hết cho các số nguyên tố 2, 3, 5. Ta có: 217 = 7 . 31. Vì thế 7 là một ước nguyên tố của 217.
II. Phân tích một số ra thừa số nguyên tố
+ Phân tích một số tự nhiên lớn hơn 1 ta thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.
Lưu ý: Khi phân tích một số ra thừa số nguyên tố ta nên chia mỗi số trong khi phân tích cho ước nguyên tố nhỏ nhất của nó.
Cứ tiếp tục chia như thế cho đến khi được thương là 1.
+ Ta có thể phân tích một số ra thừa số nguyên tố bằng cách viết “rẽ nhánh” và “theo cột dọc”.
Ví dụ: Phân tích số 40 ra thừa số nguyên tố bằng cách viết “rẽ nhánh” và “theo cột dọc”.
Lời giải:
+ Cách viết "rẽ nhánh":
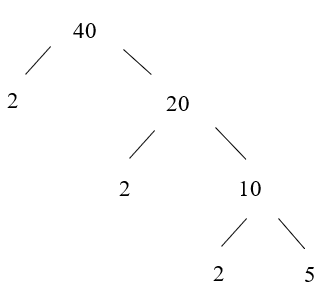
Do đó: 40 = 2 . 2 . 2 . 5 = 23 . 5
+ Cách viết "theo cột dọc":
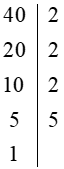
Vậy ta phân tích được: 40 = 2 . 2 . 2 . 5 = 23 . 5.
Chú ý:
+ Dạng phân tích ra thừa số nguyên tố của một số nguyên tố là chính số đó.
+ Mọi hợp số đều phân tích được ra thừa số nguyên tố.
+ Thông thường, khi phân tích một số tự nhiên ra thừa số nguyên tố, các ước nguyên tố được viết theo thứ tự tăng dần.
+ Ngoài cách làm như trên, ta cũng có thể phân tích một số ra thừa số nguyên tố bằng cách viết số đó thành tích của hai thừa số một cách linh hoạt.
Ví dụ: Phân tích số 450 ra thừa số nguyên tố.
Ta có: 450 = 9 . 50
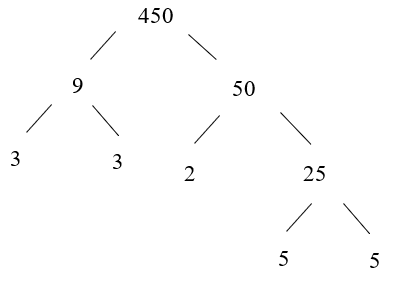
Vậy 450 = 3 . 3 . 2 . 5 . 5 = 2 . 32 . 52.
Nhận xét: Dù phân tích một số ra thừa số nguyên tố bằng cách nào thì cuối cùng ta cũng được cùng một kết quả.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
