Với giải sách bài tập Toán 6 Bài 1: Phân số với tử số và mẫu số là số nguyên sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 1: Phân số với tử số và mẫu số là số nguyên

Bài 1 trang 8 sách bài tập Toán lớp 6 Tập 2: Viết các phân số sau:

a) Âm mười bảy phần bốn mươi hai;

b) Ba mươi ba phần âm bảy mươi chín;

c) Ba trăm linh chín phần một nghìn linh một;

d) Âm bốn mươi tám phần âm hai mươi ba.

Lời giải:

a) Âm mười bảy phần bốn mươi hai có tử số là −17, mẫu số là 42.

Ta viết: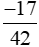 

b) Ba mươi ba phần âm bảy mươi chín có tử số là 33, mẫu số là −79.

Ta viết: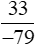 

c) Ba trăm linh chín phần một nghìn linh một có tử số là 309, mẫu số là 1001.

Ta viết: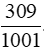 

d) Âm bốn mươi tám phần âm hai mươi ba có tử số là −48, mẫu số là −23.

Ta viết: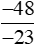 

Bài 2 trang 8 sách bài tập Toán lớp 6 Tập 2: Vẽ lại hình bên, sau đó thêm các đoạn thẳng thích hợp và tô màu vào ô cần  thiết để được hình vẽ có phần tô màu biểu thị phân số . Nêu hai cách vẽ và tô màu.

Lời giải:

Phần tô màu biểu thị phân số 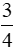 nghĩa là hình vẽ được chia thành 4 phần bằng nhau, tô màu 3 phần.

Trong hình vẽ trên, hình chữ nhật được chia thành hai phần bằng nhau. Ta có thể vẽ thêm các đoạn thẳng để tạo ra 4 phần bằng nhau, có thể làm theo hai cách sau:

- Cách 1: Vẽ thêm một đoạn thẳng “chia đôi” hình vẽ để tạo ra 4 ô giống nhau, sau đó tô màu 3 ô.

- Cách 2: Vẽ thêm hai đoạn thẳng “song song” với chiều dài hình chữ nhật để tạo ra 4 hình chữ nhật giống nhau có cùng chiều dài, sau đó tô màu 3 hình đó.

Bài 3 trang 8 sách bài tập Toán lớp 6 Tập 2: Một bể bơi có máy bơm A để bơm nước vào bể. Nếu bể không có nước máy bơm sẽ bơm đầy bể trong 7 giờ. Cũng bể bơi đó, có máy bơm B dùng để tháo nước ra khỏi bể khi vệ sinh bể bơi. Nếu bể đầy nước, máy bơm B sẽ bơm hết nước trong bể chỉ trong 5 giờ. Điền phân số với tử và mẫu là số nguyên thích hợp vào bảng sau đây:

Lời giải:

- Máy bơm A sẽ bơm từ khi chưa có nước đến khi đầy bể mất 7 giờ nên phân số ở mỗi ô có mẫu số là 7, tử số là số giờ bơm tương ứng.

- Máy bơm B sẽ tháo nước từ khi đầy bể đến khi hết sạch nước trong bể là 5 giờ nên phân số ở mỗi ô có mẫu số là 5, tử số là số âm của giờ bơm tương ứng.

Ta có bảng sau:

Bài 4 trang 8 sách bài tập Toán lớp 6 Tập 2: Thay dấu ? bằng số nguyên thích hợp

a)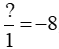 

b)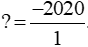 

Lời giải:

Số nguyên là một phân số có mẫu số là 1 và tử số là chính số nguyên đó.

a) Số nguyên −8 có là phân số có mẫu số là 1 và tử số là −8.

Vậy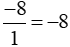 

b) Phân số  có tử số là −2020 và mẫu số là 1 nên ? = −2020 : 1 = −2020

Vậy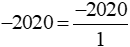 

Bài 5 trang 8 sách bài tập Toán lớp 6 Tập 2: Điền số nguyên thích hợp vào ô trống:

Lời giải:

a) Vì 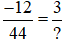 nên (−12) . ? = 44 . 3

Quy bài toán về tìm số nguyên ? biết (−12) . ? = 44 . 3

(−12) . ? = 132

? = 132 : (−12)

? = −11

Vậy ta điền: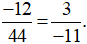 

b) Vì 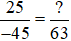 nên 25 . 63 = (−45) . ?

Quy bài toán về tìm số nguyên ? biết 25 . 63 = (−45) . ?

(−45) . ? = 25 . 63

(−45) . ? = 1575

? = 1575 : (−45)

? = −35

Vậy ta điền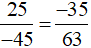 

Bài 6 trang 8 sách bài tập Toán lớp 6 Tập 2: Giải thích tại sao:

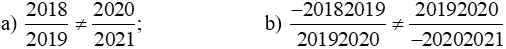
Lời giải:

Nếu a . d = b . c thì 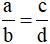 (với a, b, c, d ≠ 0).

a) Ta so sánh hai tích: 2018 . 2021 và 2019. 2020

Ta có: 

2018 . 2021 = 2018 . (2020 + 1) 

= 2018 . 2020 + 2018 . 1 

= 2018 . 2020 + 2018;

2019. 2020 = (2018 + 1). 2020 

= 2018 . 2020 + 1 . 2020

= 2018 . 2020 + 2020.

Vì 2018 < 2020 nên 2018 . 2020 + 2018 < 2018 . 2020 + 2020

Hay 2018 . 2021 < 2019. 2020.

Do đó 2018 . 2021 ≠ 2019. 2020 .

Vậy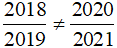 

b) Ta so sánh hai tích: (−20182019). (−20202021) và 20192020 . 20192020.

Hay so sánh 20182019. 20202021 và 20192020 . 20192020

- Xét tích 20182019. 20202021.

Nhận thấy 20182019 và 20202021 đều là số lẻ 

Nên 20182019. 20202021 cũng là số lẻ (tích của hai số lẻ là một số lẻ).

- Xét tích 20192020 . 20192020.

Nhận thấy: 20192020 là số chẵn.

Nên 20192020 . 20192020 cũng là số chẵn (tích của hai số chẵn là một số chẵn).

Vì tích 20182019. 20202021 là số lẻ, tích 20192020 . 20192020 là số chẵn 

Nên 20182019. 20202021 ≠ 20192020 . 20192020

Vậy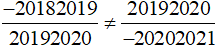 

Bài 7 trang 9 sách bài tập Toán lớp 6 Tập 2: Kiểm tra khẳng định: 18 . (−5) = (−15) . 6. Từ khẳng định đó, viết phân số bằng phân số  Cũng từ khẳng định đó, có thể có những cặp phân số nào khác mà bằng nhau?

Lời giải:

Ta thấy 18 . (−5) = 6 . 3 . (−5) = 6. (−15) = (−15) . 6

Do đó 18 . (−5) = (−15) . 6 là khẳng định đúng.

Vì 18 . (−5) = (−15) . 6 nên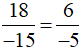 

Ta đổi chỗ lần lượt các thừa số trong hai tích ở biểu thức:

18 . (−5) = (−15) . 6

Nếu viết thành (−5) . 18 = 6 . (−15) thì ta có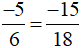 

Nếu viết thành (−5) . 18 = (−15) . 6 thì ta có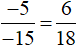 

Nếu viết thành 18 . (−5) = 6 . (−15) thì ta có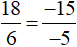 

Do đó các cặp phân số khác bằng nhau là: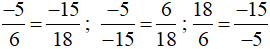 

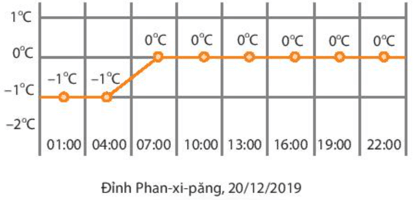
Bài 8 trang 9 sách bài tập Toán lớp 6 Tập 2: Hình dưới đây cho biết số liệu nhiệt độ ở đỉnh Phan-xi-păng trong ngày 20/12/2019. Theo em, số đo nhiệt độ trung bình trong ngày là phân số nào?

Lời giải:

Nhiệt độ trung bình trong ngày có thể coi là trung bình cộng nhiệt độ ở các thời điểm đo trong ngày. 

Phân số biểu thị nhiệt độ trung bình trong ngày có mẫu số là số lần đo và tử số là tổng nhiệt độ đo được ở các lần.

Hình vẽ trên cho biết số đo nhiệt độ trong ngày được thu thập tại 8 thời điểm, cách đều nhau 3 giờ. 

Trung bình cộng nhiệt độ ở 8 thời điểm đo trong ngày là:

[(−1) + (−1) + 0 + 0 + 0 + 0 + 0 + 0] : 8 = (−2) : 8 = .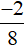

Vậy phân số biểu thị nhiệt độ trung bình trong ngày 20/12/2019 là 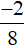^oC.

Lý thuyết  Phân số với tử số và mẫu số là số nguyên

1. Khái niệm phân số

Ta gọi 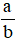, trong đó  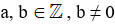là phân số, a là tử số (tử), b là mẫu số (mẫu) của phân số. Phân số  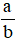đọc là a phần b.

Ví dụ 1. Phân số 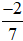 có tử số là −2, mẫu số là 7 và được đọc là “âm hai phần bảy”.

Chú ý: Ta có thể dùng phân số để ghi (viết, biểu diễn) kết quả phép chia một số nguyên cho một số nguyên khác 0.

Ví dụ 2. Phân số 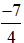 là ghi kết quả phép chia −7 cho 4.

2. Phân số bằng nhau
 Hai phân số 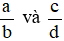 được gọi là bằng nhau, viết là 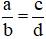, nếu a . d = b . c.

Ví dụ 3. 

a) 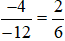 vì (−4) . 6 = (−12) . 2 (cùng bằng –24).

b)  không bằng 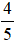, vì 3 . 5 không bằng 4 . 4. Viết .

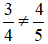Chú ý: Điều kiện a . d = b . c gọi là điều kiện bằng nhau của hai phân số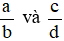  

Ví dụ 4. Các cặp phân số sau có bằng nhau hay không?

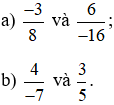
Lời giải:

a)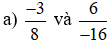 

So sánh hai tích: (−3) . (−16) và 8 . 6;

Ta có: (−3) . (−16) = 3 . 16 = 48 và 8 . 6 = 48.

Nên (−3) . (−16) = 8 . 6. Do đó .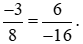

.

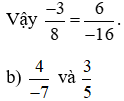So sánh hai tích: 4 . 5 và (−7) . 3;

Ta có: 4 . 5 = 20 và (−7) . 3 = −21.

Nên 4 . 5 ≠ (−7) . 3. Do đó .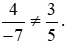

Vậy hai phân số 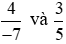 không bằng nhau.

3. Biểu diễn số nguyên ở dạng phân số 

Mỗi số nguyên n có thể coi là phân số 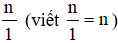. Khi đó số nguyên n được biểu diễn ở dạng phân số .

Ví dụ 5. 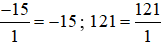.