Với giải sách bài tập Toán 6 Bài 28: Số thập phân sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 28: Số thập phân

Bài 7.1 trang 24 sách bài tập Toán lớp 6 Tập 2:a) Viết các phân số sau dưới dạng số thập phân.

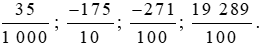
b) Tìm số đối của các số thập phân đã viết được ở câu a.

Lời giải: 

a) Cách đổi các phân số thập phân sang số thập phân thì ta quy về bài toán chia một số cho 10; 100; 1 000 (kết quả để dưới dạng số thập phân).

Quy tắc: Muốn chia một số cho 10; 100; 1 000 ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, … chữ số.

Đổi lần lượt các phân số thập phân trên ra số thập phân, ta được:

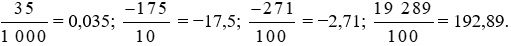
b) Cách tìm số đối của một số thập phân: ta thêm dấu trừ vào trước số thập phân đó. 

Số đối của 0,035 là –0,035;

Số đối của –17,5 là –(–17,5) = 17,5;

Số đối của –2,71 là –(–2,71) = 2,71;

Số đối của 192,89 là –192,89.

Bài 7.2 trang 25 sách bài tập Toán lớp 6 Tập 2:a) Viết các số thập phân sau dưới dạng phân số thập phân.

2,15; –8,965; –12,05; 0,025.

b) Viết các phân số sau đây dưới dạng phân số thập phân và số thập phân.

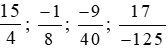
Lời giải:

a) Cách viết số thập phân sang phân số thập phân:

- Tử số: Viết phần số nguyên và phần thập phân chỉ bỏ đi dấu phẩy.

- Mẫu số: Viết số 1 trước. Đếm phần thập phân có bao nhiêu chữ số thì thêm bấy nhiêu số 0 vào bên phải số 1 

(Có thể hiểu: Tử số = Số thập phân đó nhân với 10; 100; 1 000;… 

Mẫu số là 10; 100; 1 000;… tương ứng).

Đổi lần lượt các số thập phân trên ra phân số thập phân, ta được:

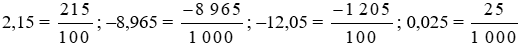
b) Nhân cả tử và mẫu của phân số với một số để thu được mẫu số là 10; 100;  1000; … Sau đó đổi các phân số thập phân vừa tìm được sang số thập phân.

Vì 100 : 4 = 25 nên nhân cả tử và mẫu của phân số 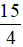 với 25, ta được:

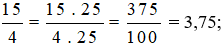
Vì 1000 : 8 = 125 nên nhân cả tử và mẫu của phân số 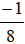 với 125, ta được:

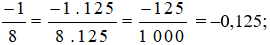
Vì 1000 : 40 = 25 nên nhân cả tử và mẫu của phân số 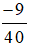 với 25, ta được:

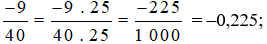
Vì 1000 : 125 = 8 nên nhân cả tử và mẫu của phân số 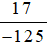 với (–8), ta được:

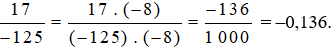
Vậy các phân số 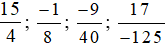 đổi sang phân số thập phân lần lượt là  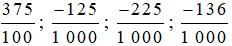và đổi sang số thập phân lần lượt là 3,75; –0,125; –0,225; –0,136.

Bài 7.3 trang 25 sách bài tập Toán lớp 6 Tập 2: So sánh các số sau:

a) 6,25 và 0,985;

b) –245,024 và 19,9989;

c) –2,6057 và –3,6049.

Lời giải:

- So sánh hai số thập phân dương: đi từ trái qua phải, so sánh các chữ số ở cùng một hàng, ta so sánh từ phần nguyên đến phần nguyên đến phần thập phân và từ chữ số hàng cao nhất đến hàng thấp nhất.

- Số âm luôn nhỏ hơn 0 và nhỏ hơn số dương.

- So sánh hai số thập phân âm: ta so sánh hai số đối của chúng, số thập phân âm nào có số đối lớn hơn số đối của số thập phân kia thì số thập phân âm đó nhỏ hơn.

a) 6,25 và 0,985

Phần nguyên của số 6,25 là 6;

Phần nguyên của số 0,985 là 0.

Vì 6 > 0  nên 6,25 > 0,985.

b) Ta thấy –245,024 là số thập phân âm;

Và 19,9989 là số thập phân dương.

Do đó –245,024 < 19,9989 (số thập phân âm nhỏ hơn số thập phân dương).

c) Số đối của số –2,6057 là –(–2,6057) = 2,6057;

Số đối của số –3,6049 là –(–3,6049) = 3,6049.

Vì 2,6057 < 3,6049 nên –2,6057 > –3,6049.

Bài 7.4 trang 25 sách bài tập Toán lớp 6 Tập 2: Tìm số nguyên x, biết 254,12 < x < 259,7

Lời giải:

Bài toán yêu cầu tìm số nguyên nên ta xét phần nguyên của hai số trên.

Phần nguyên của số 254,12 là 254;

Phần nguyên của số 259,7 là 259.

Đưa bài toán về tìm số nguyên thỏa mãn: 254 < x  259

Các số nguyên x thỏa mãn điều kiện trên là: 255; 256; 257; 258; 259.

Vậy các số nguyên thỏa mãn 254,12 < x < 259,7 là x {255; 256; 257; 258; 259}.

Bài 7.5 trang 25 sách bài tập Toán lớp 6 Tập 2: Tìm tập hợp các số thập phân x có một chữ số sau dấu phẩy thỏa mãn:

Lời giải:

a) x nằm giữa 3,27 và 3,63;

b) –5,84 < x < –5,43.

Lời giải: 

a) Các số thập phân x có một chữ số sau dấu phẩy thỏa mãn là: 3,3; 3,4; 3,5; 3,6.

Vậy tập hợp các số thập phân x thỏa mãn x nằm giữa 3,27 và 3,63 là: 

x {3,3; 3,4; 3,5; 3,6}.

b) Số đối của số –5,84 là 5,84;

Số đối của số –5,43 là 5,43.

Các số thập phân x có một chữ số sau dấu phẩy thỏa mãn 5,84 > x > 5,43 là 5,8; 5,7; 5,6; 5,5.

Do đó, các số thập phân x có một chữ số sau dấu phẩy thỏa mãn –5,84 < x < –5,43 là –5,8; –5,7; –5,6; –5,5.

Vậy tập hợp các số thập phân x thỏa mãn –5,84 < x < –5,43 là:

x {–5,8; –5,7; –5,6; –5,5}.

Bài 7.6 trang 25 sách bài tập Toán lớp 6 Tập 2: Theo bảng xếp hạng 100 thương hiệu quốc gia giá trị nhất thế giới năm 2020 của Brand Finance, thương hiệu quốc gia Việt Nam tăng vọt hơn 29% lên 319 tỉ USD, đạt mức tăng trưởng cao nhất thế giới.

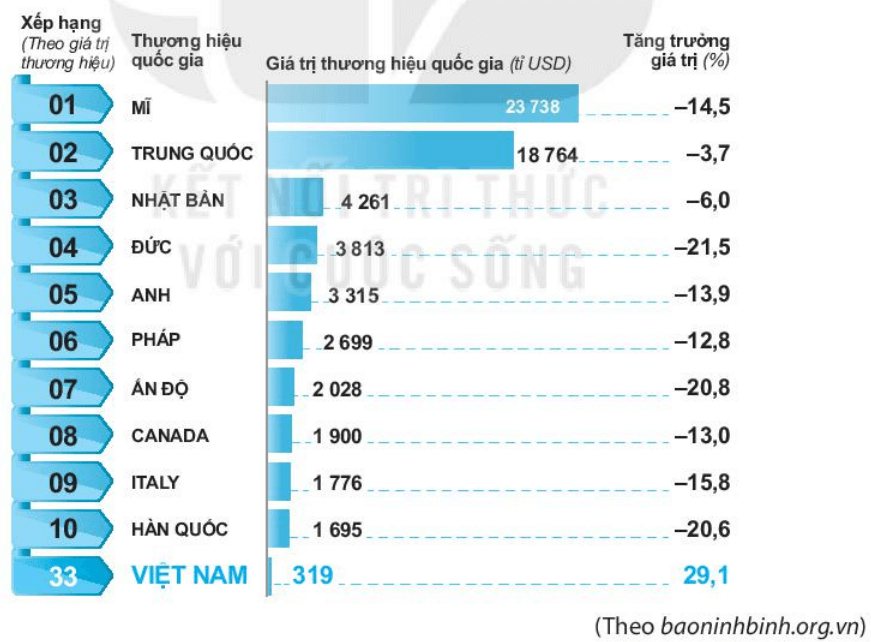
Căn cứ vào bảng trên, em hãy sắp xếp theo thứ tự từ cao đến thấp mức tăng trưởng giá trị thương hiệu quốc gia của 11 quốc gia có tên trong bảng trên.

Lời giải:

Dựa vào bảng trên, ta thấy mức tăng trưởng giá trị thương hiệu quốc gia của Mĩ, Trung Quốc, Nhật Bản, Đức, Anh, Pháp, Ấn Độ, Canada, Italy, Hàn Quốc và Việt Nam lần lượt là –14,5; –3,7; –6,0; –21,5; –13,9; –12,8; –20,8; –13,0; –15,8; –20,6; 29,1.

Đưa bài toán về sắp xếp các số trên theo thứ tự từ lớn đến bé.

- Trong dãy số trên chỉ có số 29,1 là số dương nên là số lớn nhất.

- Số đối của các số –14,5; –3,7; –6,0; –21,5; –13,9; –12,8; –20,8; –13,0; –15,8; –20,6 lần lượt là 14,5; 3,7; 6,0; 21,5; 13,9; 12,8; 20,8; 13,0; 15,8; 20,6.

+ Hai số 13,9 và 13,0 đều có phần nguyên là 13 và phần thập phân lần lượt là 9 và 0. Vì 9 > 0 nên 13,9 > 13,0.

+ Các số thập phân còn lại đều có phần nguyên khác nhau nên ta so sánh phần nguyên của chúng.

Vì –3,7 < –6,0 < –12,8 < –13 < –13,9 < –14,5 < –15,8 < –20,6 < –20,8 < –21,5 nên  –3,7 > –6,0 > –12,8 > –13 > –13,9 > –14,5 > –15,8 > –20,6 > –20,8 > –21,5.

Từ đó ta suy ra 29,1 > –3,7 > –6,0 > –12,8 > –13 > –13,9 > –14,5 > –15,8 > –20,6 > –20,8 > –21,5.

Vậy mức tăng trưởng giá trị thương hiệu quốc gia của 11 quốc gia có tên trong bảng trên được sắp xếp theo thứ tự từ cao đến thấp là: Việt Nam, Trung Quốc, Nhật Bản, Pháp, Canada, Anh, Mĩ, Italy, Hàn Quốc, Ấn Độ, Đức.

Bài 7.8 trang 25 sách bài tập Toán lớp 6 Tập 2: Tìm tất cả các cặp chữ số (a; b) biết rằng .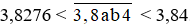

Lời giải:

Nhân cả ba số 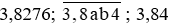 với 1 000, ta tìm được các giá trị lần lượt là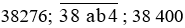 

Đưa bài toán trên về tìm cặp chữ số (a; b) thỏa mãn:

Vậy các cặp chữ số (a; b) cần tìm là: (2; 8); (2; 9); (3; 0); (3; 1); (3; 2); (3;3); (3; 4); (3; 5); (3; 6); (3; 7); (3; 8); (3; 9).

Lý thuyết Số thập phân

1. Phân số thập phân và số thập phân

a) Phân số thập phân.

– Phân số thập phân là phân số có phần mẫu số là lũy thừa của 10

Ví dụ 1: 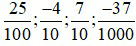 … được gọi là các phân số thập phân

Các phân số 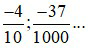  là các phân số thập phân âm.

Các phân số 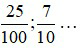  là các phân số thập phân dương.

b) Số thập phân

Ta viết 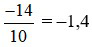  là số thập phân âm, đọc là “âm một phẩy bốn”.

Ta viết 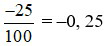  là số thập phân âm, đọc là “âm không phẩy hai mươi lăm”.

Ta viết 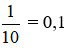  là số thập phân dương, đọc là “không phẩy một”.

– Các số –0,3; –1,6; –3.76… là các số thập phân âm.

– Các số 0,17; 1, 89; 3, 15… là các số thập phân dương.

– Các số thập phân âm và và các số thập phân dương gọi chung là các số thập phân.

– Các số 1, 7 và –1, 7; 3, 2 và –3, 2… gọi là hai số đối nhau.

c) Tính chất của số thập phân

- Mỗi số thập phân gồm: Phần số nguyên viết bên trái dấu “,”; phần thập phân viết bền phải dấu “,”.

- Nếu thêm chữ số 0 vào bên phải phần thập phân của một số thập phân thì số thập phân không đổi: 

21, 45 = 21, 450 = 21, 4500 = …

- Hai số thập phân được gọi là đối nhau nếu tổng của chúng bằng 0.

d) Đổi từ số thập phân ra phân số và ngược lại.

– Đổi từ số thập phân sang phân số ta làm như sau:

Bước 1: Đếm xem có bao nhiêu số ở phía bên phải dấu phẩy. Gọi n là số chữ số ở phía bên phải dấu phẩy.

Bước 2: Bỏ đi dấu phẩy và viết số không có dấu phẩy ở tử số; lũy thừa 10ⁿ ở mẫu số.

Bước 3: Rút gọn phân số phía trên để được phân số tối giãn.

Ví dụ 2: Đổi 0, 14 sang phân số ta làm như sau:

Ta đếm thấy bên phải dấu phẩy của số 0, 14 có 2 số là 1 và 4. Số 0, 14 sau khi bỏ dấu phẩy là 14

Vậy đổi 0, 14 ra phân số thập phân là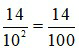  

Ta rút gọn phân số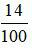  

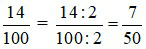
– Đổi phân số ra số thập phân

Bước 1: Đưa phân số về dạng phân số thập phân có mẫu là lũy thừa của 10

Bước 2: Kiểm tra xem mẫu số là lũy thừa mấy của 10. Giả sử mẫu số là lũy thừa bậc n của 10.

Bước 3: Đếm từ phải sang tới số thứ n của tử và đặt dấu phẩy ở đó, số thập phân cần tìm là số ở tử khi đã đặt dấu phẩy

Ví dụ 3: Đổi 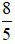  ra số thập phân

Ta có: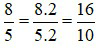  

Mẫu số là lũy thừa cơ số 1 của 10.

Ta đếm từ phải sang và đặt dấu phẩy trước số thứ nhất của tử ta được 1, 6

Vậy đổi 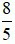  sang số thập phân ta được kết quả là 1, 6.

2. So sánh hai số thập phân

a) So sánh hai số thập phân dương

Muốn so sánh hai số thập phân ta có thể làm như sau:

– So sánh các phần nguyên của hai số đó như so sánh hai số tự nhiên, số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.

– Nếu phần nguyên của hai số đó bằng nhau thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn ... đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn.

– Nếu phần nguyên và phần thập phân của hai số đó bằng nhau thì hai số đó bằng nhau.

Ví dụ 4: So sánh

a) 3, 56 và 7,37

b) 4,25 và 4,35

Lời giải: 

a) Ta so sánh phần nguyên: Ta thấy 3 < 7 nên 3, 56 < 7,37

b) Ta so sánh phần nguyên: Ta thấy 4 = 4 do đó ta chuyển sang so sánh phần thập phân, bắt đầu từ phần mười: 

Ta thấy 2 < 3 nên 4, 25 < 4, 35.

b) So sánh hai số thập phân âm

– Nếu a, b là hai số thập phân dương và a > b thì –a < –b

Chú ý: Số thập phân âm luôn nhỏ hơn 0 và nhỏ hơn số thập phân dương.

Số thập phân dương luôn lớn hơn 0 và lớn hơn số thập phân âm.

Ví dụ 5: So sánh

a) 0, 745 và –1, 234

b) –2, 13 và –3, 12

Lời giải: 

a) 0, 745 và –1, 234

Vì 0, 745 là số thập phân dương và –1, 234 là số thập phân âm nên 0, 745 > –1, 234.

b) –2, 13 và –3, 12

Ta đi so sánh 2, 13 và 3, 12

Vì 2 < 3 nên 2, 13 < 3, 12 nên –2, 13 > –3, 12.