Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 6 Số thập phân được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 6. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Số thập phân. Mời các bạn đón xem:
Bài tập Toán 6 Số thập phân
A. Bài tập Số thập phân
Bài 1: Đổi các phân số thập phân sau ra số thập sau: 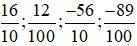
Lời giải:
Ta có:
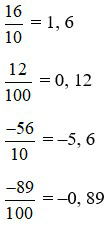
Bài 2: Đổi các số thập phân –0, 14; –5, 6; 7, 8; 11, 8 ra phân số thập phân.
Lời giải:
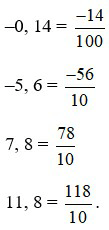
Bài 3: Đọc các số thập phân sau: –0, 14; 1, 23; 4, 56; –122, 25
Lời giải:
–0, 14 đọc là “âm không phẩy mười bốn”
1, 23 đọc là “một phẩy hai mươi ba”
4, 56 đọc là “bốn phẩy năm mươi sáu”
–122, 25 đọc là “âm một trăm hai mươi hai phẩy hai mươi lăm”
Bài 4: So sánh
a) 3, 14 và –5, 67
b) –26, 13 và –26, 31
Lời giải:
a) 3, 14 và –5, 67
Ta có: 3, 14 là số thập phân dương, –5, 67 là số thập phân âm do đó 3, 14 > –5, 67.
b) –26, 13 và –26, 31
Ta đi so sánh 26, 13 và 26, 31
Ta có phần nguyên 26 = 26 nên ta sẽ so sánh đến phần thập phân
Vì 1 < 3 nên 26, 13 < 26, 31 do đó –26, 13 > –26, 31.
Bài 5. Viết các phân số sau dưới dạng số thập phân:
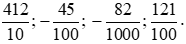
Lời giải:
Các phân số trên đều là phân số thập phân.
Cách đổi các phân số thập phân sang số thập phân thì ta quy về bài toán chia một số cho 10; 100; 1 000 (kết quả để dưới dạng số thập phân).
Quy tắc: Muốn chia một số cho 10; 100; 1 000 ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, … chữ số.
Đổi lần lượt các phân số thập phân trên ra số thập phân, ta được:
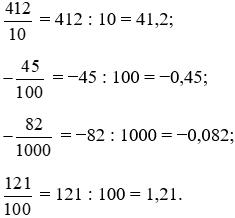
Bài 6. Viết các số thập phân sau đây dưới dạng phân số thập phân:
−14,5; 25,12; −32,46; −0,785.
Lời giải:
- Các phân số thập phân được viết dưới dạng số thập phân.
- Số các chữ số thập phân bằng đúng số các chữ số 0 ở mẫu của phân số thập phân.
Đổi lần lượt các số thập phân trên ra phân số thập phân, ta được:
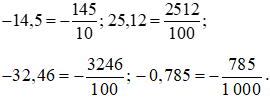
Bài 7. Tìm số đối của các số thập phân sau:
34,18; −26,8; −0,465; 2,4.
Lời giải:
Cách tìm số đối của một số thập phân: ta thêm dấu trừ vào trước số thập phân đó.
Số đối của 34,18 là −34,18;
Số đối của −26,8 là −(−26,8) hay 26,8;
Số đối của −0,465 là −(−0,465) = 0,465;
Số đối của 2,4 là −2,4.
Bài 8: Hãy sắp xếp các số sau theo thứ tự giảm dần:
0,6; −24,45; −24,15; 35,18; 21,75.
Lời giải:
Để sắp xếp các số thập phân sau theo thứ tự giảm dần, ta làm như sau:
Bước 1: Chia thành 2 nhóm số thập dương và số thập phân âm, vì số thập phân âm luôn nhỏ hơn số thập phân dương.
Bước 2: Ta so sánh các số thập phân theo nhóm với nhau:
- Nhóm các số thập phân dương: ta so sánh phần nguyên với nhau, số nào có phần nguyên lớn hơn thì lớn hơn. Nếu phần nguyên bằng nhau thì ta lần lượt so sánh các hàng ở phần thập phân.
- Nhóm các số thập phân âm: ta so sánh số đối của chúng, số nào có số đối lớn hơn thì nhỏ hơn.
Sắp xếp các số thập phân sau theo thứ tự giảm dần:
* Phân loại:
- Nhóm các số thập phân dương: 0,6; 35,18; 21,75.
- Nhóm các số thập phân âm: −24,45; −24,15.
* So sánh các số thập phân trong theo nhóm:
- Nhóm các số thập phân dương: ta so sánh phần nguyên của các số trên.
Vì 35 > 21 > 0 nên 35,18 > 21,75 > 0,6.
- Nhóm các số thập phân âm: Số đối của các số −24,45; −24,15 lần lượt là 24,45; 24,15.
+ Phần nguyên của hai số 24,45; 24,15 đều là 24.
+ Ta so sánh phần thập phân của hai số. Hàng phần mười của số 24,45; 24,15 lần lượt là 4 và 1.
Vì 1 < 4 nên 24,15 < 24,45, hay −24,15 > −24,45.
Do đó 35,18 > 21,75 > 0,6 > −24,15 > −24,45.
Vậy các số được sắp xếp thứ tự giảm dần là: 35,18; 21,75; 0,6; −24,15; −24,45.
Bài 9. Cho các phân số và hỗn số: ; ;
a) Viết các phân số và hỗn số trên dưới dạng phân số thập phân;
b) Sắp xếp các số thập phân tìm được ở câu a theo thứ tự tăng dần.
Hướng dẫn giải
a) Ta có: ;
;
Vậy
b) Ta chia các số ‒0,3; ‒0,14; 1,152; 0,027; 0,875 thành hai nhóm:
Nhóm 1 gồm các số: ‒0,3; ‒0,14
Nhóm 2 gồm các số 1,152; 0,027; 0,875.
Ta đi so sánh nhóm 1: ‒0,3; ‒0,14
Xét hai số 0,3 và 0,14: Kể từ trái sang phải, cặp chữ số đầu tiên khác nhau của hai số trên là hàng phần mười. Mà 3 > 1 nên 0,3 > 0,14 do đó ‒0,3 < ‒0,14.
Ta đi so sánh nhóm 2: 1,152; 0,027; 0,875.
Xét hai số 0,027 và 0,875: Kể từ trái sang phải, cặp chữ số đầu tiên khác nhau của hai số này là hàng phần mười. Mà 0 < 8 nên 0,027 < 0,875.
Xét hai số 0,875 và 1,152: Ta thấy phần nguyên của hai số là 0 < 1 nên 0,875 < 1,152.
Suy ra 0,027 < 0,875 < 1,152
Nhóm 1 gồm các số âm và nhóm 2 gồm các số dương. Mà số âm luôn nhỏ hơn số dương.
Do đó ta có ‒0,3 < ‒0,14 < 0,027 < 0,875 < 1,152.
Vậy sắp xếp các số thập phân theo thứ tự tăng dần là ‒0,3; ‒0,14; 0,027; 0,875; 1,152.
Bài 10. Viết các số thập phân sau dưới dạng phân số tối giản có mẫu số dương:
‒35,45; 0,79; ‒0,068.
Hướng dẫn giải
Ta có: ‒35,45 ;
0,79 ;
‒0,068 .
Bài 11. Biết nhiệt độ đông đặc của thuỷ ngân là ‒38,83°C, của rượu là ‒114,1°C, của băng phiến là 80,26°C và của nước là 0°C.
Hãy cho biết nhiệt độ đông đặc của chất nào là thấp nhất?
Hướng dẫn giải
Ta so sánh hai số ‒38,83 và ‒114,1:
Xét hai số 38,83 và 114,1 ta thấy phần nguyên của hai số là 38 < 114 nên 38,83 < 114,1 suy ra ‒38,83 > ‒114,1
Ta thấy nhiệt độ đông đặc của thuỷ ngân (‒38,83°C) và của rượu (‒114,1°C) là số thập phân âm; nhiệt độ đông đặc của băng phiến (80,26°C ) là số thập phân dương và của nước là số 0.
Mà số 0 luôn lớn hơn số thập phân âm và nhỏ hơn số thập phân dương.
Do đó ta có: ‒114,1 < ‒38,83 < 0 < 80,26
Hay ‒114,1°C < ‒38,83°C < 0°C < 80,26°C.
Vậy nhiệt độ đông đặc của rượu là thấp nhất.
Câu 12. Trong một cuộc thi chạy 200 m, có ba vận động viên đạt thành tích cao nhất là:
Mai Anh: 31,42 giây; Ngọc Mai: 31,48 giây; Phương Hà: 31,09 giây.
Các vận động viên đã về Nhất, về Nhì, về Ba lần lượt là:

A. Ngọc Mai, Mai Anh, Phương Hà.
B. Ngọc Mai, Phương Hà, Mai Anh.
C. Phương Hà, Mai Anh, Ngọc Mai.
D. Mai Anh, Ngọc Mai, Phương Hà.
Trả lời:
Ta có: 31,48 > 31,42 > 31,09.
Suy ra Ngọc Mai về nhất, Mai Anh về nhì, Phương Hà về ba.
Đáp án cần chọn là: A
Câu 13. Viết các phân số và hỗn số sau dưới dạng số thập phân:
A. −0,09; −0,625; 3,08
B. −0,009; −0,625; 3,08
C. −0,9; −0,625; 3,08
D. −0,009; −0,625; 3,008
Trả lời:
Đáp án cần chọn là: B
Câu 14. Viết các số sau theo thứ tự giảm dần:
−120,341; 36,095; 36,1; −120,34.
A. 36,095 > 36,100 > −120,34 > −120,341
B. 36,095 > 36,100 > −120,341 > −120,34
C. 36,100 > 36,095 > −120,341 > −120,34
D. 36,100 > 36,095 > −120,34 > −120,341
Trả lời:
Ta có:
36,100 > 36,095 nên 36,1 > 36,095.
−120,340 > −120,341 nên −120,34 > −120,341
⇒ 36,100 > 36,095 > −120,34 > −120,341.
Đáp án cần chọn là: D
Câu 15. Số đối của các số thập phân sau lần lượt là:
9,32; −12,34; −0,7; 3,333
A. 9,32; −12,34; −0,7; 3,333
B. −9,32; 12,34; 0,7; 3,333
C. −9,32; 12,34; 0,7; −3,333
D. −9,32; −12,34; 0,7; −3,333
Trả lời:
Số đối của 9,32 là −9,32
Số đối của −12,34 là 12,34
Số đối của −0,7 là 0,7
Số đối của 3,333 là −3,333
Vậy ta được: −9,32; 12,34; 0,7; −3,333.
Đáp án cần chọn là: C
Câu 16: Viết các phân số và hỗn số sau dưới dạng số thập phân:
A. −0,09; −0,625; 3,08
B. −0,009; −0,625; 3,08
C. −0,9; −0,625; 3,08
D. −0,009; −0,625; 3,008
Trả lời:
Đáp án cần chọn là: B
Câu 17: Các phân số được viết dưới dạng số thập phân theo lần lượt là
A. 0,69; 0,877; 3,4567
B. 0,69; 8,77; 3,4567
C. 0,069; 0,877; 3,4567
D. 0,069; 8,77; 3,4567
Trả lời:
Vậy các số thập phân viết theo thứ tự là 0,069;8,77;3,4567
Đáp án cần chọn là: D
Câu 18.
Điền dấu ">;<;=" vào ô trống
508,99…….509,01
Trả lời:
Ta có: 508 < 509 nên 508,99 < 509,01
Câu 19. Viết các số sau theo thứ tự giảm dần: −120,341; 36,095; 36,1; −120,34.
A. 36,095 > 36,100 > −120,34 > −120,341
B. 36,095 > 36,100 > −120,341 > −120,34
C. 36,100 > 36,095 > −120,341 > −120,34
D. 36,100 > 36,095 > −120,34 > −120,341
Trả lời:
Ta có:
36,100 > 36,095 nên 36,1 > 36,095
−120,340 > −120,341 nên −120,34 > −120,341
⇒ 36,100 > 36,095 > −120,34 > −120,341.
Đáp án cần chọn là: D
Câu 20. Mỗi đơn vị của một hàng bằng bao nhiêu đơn vị của hàng thấp hơn liền sau?
A. 0,01 đơn vị
B. 0,1 đơn vị
C. 10 đơn vị
D. 100 đơn vị
Trả lời:
Mỗi đơn vị của một hàng bằng 1010 đơn vị của hàng thấp hơn liền sau.
B. Lý thuyết Số thập phân
1. Phân số thập phân và số thập phân
a) Phân số thập phân.
– Phân số thập phân là phân số có phần mẫu số là lũy thừa của 10
Ví dụ 1: 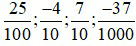 … được gọi là các phân số thập phân
… được gọi là các phân số thập phân
Các phân số 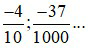 là các phân số thập phân âm.
là các phân số thập phân âm.
Các phân số 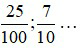 là các phân số thập phân dương.
là các phân số thập phân dương.
b) Số thập phân
Ta viết 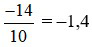 là số thập phân âm, đọc là “âm một phẩy bốn”.
là số thập phân âm, đọc là “âm một phẩy bốn”.
Ta viết 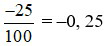 là số thập phân âm, đọc là “âm không phẩy hai mươi lăm”.
là số thập phân âm, đọc là “âm không phẩy hai mươi lăm”.
Ta viết 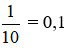 là số thập phân dương, đọc là “không phẩy một”.
là số thập phân dương, đọc là “không phẩy một”.
– Các số –0,3; –1,6; –3.76… là các số thập phân âm.
– Các số 0,17; 1, 89; 3, 15… là các số thập phân dương.
– Các số thập phân âm và và các số thập phân dương gọi chung là các số thập phân.
– Các số 1, 7 và –1, 7; 3, 2 và –3, 2… gọi là hai số đối nhau.
c) Tính chất của số thập phân
- Mỗi số thập phân gồm: Phần số nguyên viết bên trái dấu “,”; phần thập phân viết bền phải dấu “,”.
- Nếu thêm chữ số 0 vào bên phải phần thập phân của một số thập phân thì số thập phân không đổi:
21, 45 = 21, 450 = 21, 4500 = …
- Hai số thập phân được gọi là đối nhau nếu tổng của chúng bằng 0.
d) Đổi từ số thập phân ra phân số và ngược lại.
– Đổi từ số thập phân sang phân số ta làm như sau:
Bước 1: Đếm xem có bao nhiêu số ở phía bên phải dấu phẩy. Gọi n là số chữ số ở phía bên phải dấu phẩy.
Bước 2: Bỏ đi dấu phẩy và viết số không có dấu phẩy ở tử số; lũy thừa 10n ở mẫu số.
Bước 3: Rút gọn phân số phía trên để được phân số tối giãn.
Ví dụ 2: Đổi 0, 14 sang phân số ta làm như sau:
Ta đếm thấy bên phải dấu phẩy của số 0, 14 có 2 số là 1 và 4. Số 0, 14 sau khi bỏ dấu phẩy là 14
Vậy đổi 0, 14 ra phân số thập phân là 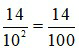
Ta rút gọn phân số 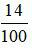
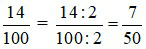
– Đổi phân số ra số thập phân
Bước 1: Đưa phân số về dạng phân số thập phân có mẫu là lũy thừa của 10
Bước 2: Kiểm tra xem mẫu số là lũy thừa mấy của 10. Giả sử mẫu số là lũy thừa bậc n của 10.
Bước 3: Đếm từ phải sang tới số thứ n của tử và đặt dấu phẩy ở đó, số thập phân cần tìm là số ở tử khi đã đặt dấu phẩy
Ví dụ 3: Đổi 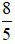 ra số thập phân
ra số thập phân
Ta có: 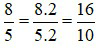
Mẫu số là lũy thừa cơ số 1 của 10.
Ta đếm từ phải sang và đặt dấu phẩy trước số thứ nhất của tử ta được 1, 6
Vậy đổi 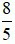 sang số thập phân ta được kết quả là 1, 6.
sang số thập phân ta được kết quả là 1, 6.
2. So sánh hai số thập phân
a) So sánh hai số thập phân dương
Muốn so sánh hai số thập phân ta có thể làm như sau:
– So sánh các phần nguyên của hai số đó như so sánh hai số tự nhiên, số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.
– Nếu phần nguyên của hai số đó bằng nhau thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn ... đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn.
– Nếu phần nguyên và phần thập phân của hai số đó bằng nhau thì hai số đó bằng nhau.
Ví dụ 4: So sánh
a) 3, 56 và 7,37
b) 4,25 và 4,35
Lời giải:
a) Ta so sánh phần nguyên: Ta thấy 3 < 7 nên 3, 56 < 7,37
b) Ta so sánh phần nguyên: Ta thấy 4 = 4 do đó ta chuyển sang so sánh phần thập phân, bắt đầu từ phần mười:
Ta thấy 2 < 3 nên 4, 25 < 4, 35.
b) So sánh hai số thập phân âm
– Nếu a, b là hai số thập phân dương và a > b thì –a < –b
Chú ý: Số thập phân âm luôn nhỏ hơn 0 và nhỏ hơn số thập phân dương.
Số thập phân dương luôn lớn hơn 0 và lớn hơn số thập phân âm.
Ví dụ 5: So sánh
a) 0, 745 và –1, 234
b) –2, 13 và –3, 12
Lời giải:
a) 0, 745 và –1, 234
Vì 0, 745 là số thập phân dương và –1, 234 là số thập phân âm nên 0, 745 > –1, 234.
b) –2, 13 và –3, 12
Ta đi so sánh 2, 13 và 3, 12
Vì 2 < 3 nên 2, 13 < 3, 12 nên –2, 13 > –3, 12.