Xét tính đơn điệu của hàm số f(x) = x^3 - 6x^2 + 9x

Xét tính đơn điệu của hàm số f(x) = x^3 - 6x^2 + 9x

Trịnh Thị Thu Hiền Ngày: 10-05-2024 Lớp 12

135

Với giải Thực hành 2 trang 9 Toán 12 Tập 1 Chân trời sáng tạo chi tiết trong Bài 1: Tính đơn diệu và cực trị của hàm số giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 12. Mời các bạn đón xem:

Giải bài tập Toán 12 Bài 1: Tính đơn diệu và cực trị của hàm số

Thực hành 2 trang 9 Toán 12 Tập 1: Xét tính đơn điệu của các hàm số sau:

a) $f (x) = x^{3} - 6 x^{2} + 9 x$

b) $g (x) = \frac{1}{x}$

Lời giải:

a) $f (x) = x^{3} - 6 x^{2} + 9 x$

Tập xác định: $D = R$

$f^{'} (x) = 3 x^{2} - 12 x + 9$

$f^{'} (x) = 0 \Leftrightarrow [\begin{array}{l} x = 3 \\ x = 1 \end{array}$

Bảng biến thiên:

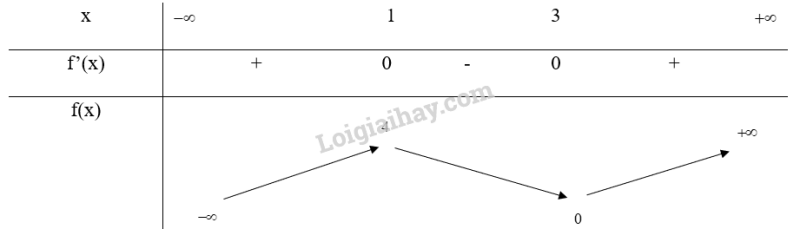
Giải SGK Toán 12 Bài 1 (Chân trời sáng tạo): Tính đơn diệu và cực trị của hàm số (ảnh 3)

Vậy hàm số $f (x) = x^{3} - 6 x^{2} + 9 x$ đồng biến trên các khoảng ( $- \infty$ ; 1) và (0; $+ \infty$ ), nghịch biến trên khoảng (1; 3)

b) $g (x) = \frac{1}{x}$

Tập xác định: $D = R ∖ {0}$

$g^{'} (x) = - \frac{1}{x^{2}}$

Vì $x^{2} > 0 \forall x \in R ∖ {0}$ nên $g^{'} (x) < 0 \forall x \in R ∖ {0}$

Bảng biến thiên:

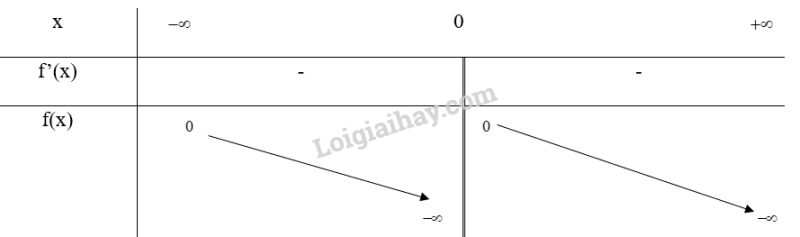
Giải SGK Toán 12 Bài 1 (Chân trời sáng tạo): Tính đơn diệu và cực trị của hàm số (ảnh 4)

Vậy hàm số $g (x) = \frac{1}{x}$ nghịch biến trên các khoảng ( $- \infty$ ; 0) và (0; $+ \infty$ )

Xem thêm lời giải bài tập Toán lớp 12 Chân trời sáng tạo hay, chi tiết khác:

Thực hành 1 trang 7 Toán 12 Tập 1: Tìm các khoảng đơn điệu của hàm số y = f(x) có đồ thị cho ở Hình 3......

Hoạt động khám phá 1 trang 7 Toán 12 Tập 1: Cho hàm số y = f(x) = $x^{2}$ .....

Thực hành 2 trang 9 Toán 12 Tập 1: Xét tính đơn điệu của các hàm số sau:.....

Thực hành 3 trang 9 Toán 12 Tập 1: Chứng minh rằng hàm số $f (x) = 3 x - s i n x$ đồng biến trên $R$ ......

Vận dụng 1 trang 9 Toán 12 Tập 1: Hãy trả lời câu hỏi trong Khởi động (trang 6) bằng cách xét dấu đạo hàm của hàm số $h (t) = 6 t^{3} - 81 t^{2} + 324 t$ với $0 \leq t \leq 8$ .......

Hoạt động khám phá 2 trang 10 Toán 12 Tập 1: Quan sát đồ thị của hàm số $y = f (x) = x^{3} - - 3 x^{2} + 1$ trong Hình 5.......

Thực hành 4 trang 11 Toán 12 Tập 1: Tìm các điểm cực trị của hàm số y = f(x) có đồ thị cho ở Hình 8......

Hoạt động khám phá 3 trang 11 Toán 12 Tập 1: Đồ thị của hàm số $y = {\begin{cases} x^{2} k h i x \leq 1 \\ 2 - x k h i x > 1 \end{cases}$ được cho ở Hình 9......

Thực hành 5 trang 12 Toán 12 Tập 1: Tìm cực trị của hàm số $g (x) = \frac{x^{2} + x + 4}{x + 1}$ ......

Vận dụng 2 trang 12 Toán 12 Tập 1: Một phần lát cắt của dãy núi có độ cao tính bằng mét được mô tả bởi hàm số .....

Bài 1 trang 13 Toán 12 Tập 1: Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 11......

Bài 2 trang 13 Toán 12 Tập 1: Xét tính đơn điệu và tìm điểm cực trị của các hàm số sau.....

Bài 3 trang 13 Toán 12 Tập 1: Tìm cực trị của các hàm số sau......

Bài 4 trang 13 Toán 12 Tập 1: Chứng minh rằng hàm số $y = \frac{2 x + 1}{x - 3}$ nghịch biến trên từng khoảng xác định của nó.....

Bài 5 trang 13 Toán 12 Tập 1: Kim ngạch xuất khẩu rau quả của Việt Nam trong các năm từ 2010 đến 2017 có thể được tính xấp xỉ bằng công thức $f (x) = 0, 01 x^{3} - - 0, 04 x^{2} + 0, 25 x + 0, 44$ (tỉ USD) với x là số năm tính từ 2010 đến 2017 ( $0 \leq x \leq 7$ ).....

Bài 6 trang 13 Toán 12 Tập 1: Xét một chất điểm chuyển động dọc theo trục $O x$ . Toạ độ của chất điểm tại thời điểm $t$ được xác định bởi hàm số $x (t) = t^{3} - 6 t^{2} + 9 t$ với $t \geq 0$ . Khi đó $x^{'} (t)$ là vận tốc của chất điểm tại thời điểm $t$ , kí hiệu $v (t)$ ; $v^{'} (t)$ là gia tốc chuyển động của chất điểm tại thời điểm $t$ , kí hiệu $a (t)$ .....

Bài 7 trang 13 Toán 12 Tập 1: Đạo hàm f '(x) của hàm số y = f(x) có đồ thị như Hình 12. Xét tính đơn điệu và tìm điểm cực trị của hàm số y = f(x).......

Xem thêm các bài giải bài tập Toán lớp 12 Chân trời sáng tạo hay, chi tiết khác:

Bài 1. Tính đơn diệu và cực trị của hàm số

Bài 2. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số

Bài 3. Đường tiệm cận của đồ thị hàm số

Bài 4. Khảo sát và vẽ đồ thị một số hàm số cơ bản

Bài tập cuối chương I

Bài 1. Vectơ và các phép toán trong không gian

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 9

Hai khối học sinh lớp 8 và lớp 9 của một trường trung học cơ sở tham gia lao động

Hai khối học sinh lớp 8 và lớp 9 của một trường trung học cơ sở tham gia lao động Lữ Ngọc My My

31

Toán Lớp 9

Bác Hương gửi tiết kiệm ngân hàng 100 triệu đồng với kì hạn 12 tháng

Bác Hương gửi tiết kiệm ngân hàng 100 triệu đồng với kì hạn 12 tháng Lữ Ngọc My My

33

Toán Lớp 9

Các kĩ sư đảm bảo an toàn của đường cao tốc thường sử dụng công thức d = 0,05v^2 + 1,1v

Các kĩ sư đảm bảo an toàn của đường cao tốc thường sử dụng công thức d = 0,05v^2 + 1,1v Lữ Ngọc My My

27

Toán Lớp 9

Tìm hai số u và v, biết: u + v = 13 và uv = 40; u – v = 4 và uv = 77

Tìm hai số u và v, biết: u + v = 13 và uv = 40; u – v = 4 và uv = 77 Lữ Ngọc My My

32

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.