Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 12 Bài 2: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số chi tiết sách Toán 12 Tập 1 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 12. Mời các bạn đón xem:
Giải bài tập Toán 12 Bài 2: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
1. Định nghĩa
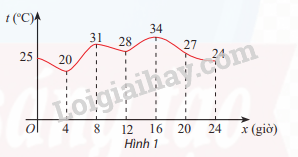
a) Khẳng định nào sau đây đúng? Vì sao?
i) Nhiệt độ cao nhất trong ngày là .
ii) Nhiệt độ cao nhất trong ngày là .
iii) Nhiệt độ cao nhất trong ngày là .
b) Hãy xác định thời điểm có nhiệt độ cao nhất trong ngày.
c) Nhiệt độ thấp nhất trong ngày là bao nhiêu?
Lời giải:
a) Khẳng định đúng là iii) vì nhìn hình ta thấy điểm cao nhất của đồ thị là
b) Thời điểm có nhiệt độ cao nhất trong ngày () là lúc 16 giờ
c) Nhiệt độ thấp nhất trong ngày là
Thực hành 1 trang 16 Toán 12 Tập 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) trên đoạn [0;3]
b) trên khoảng (0;5)
c)
Lời giải:
a) Xét trên đoạn [0;3]
Bảng biến thiên:
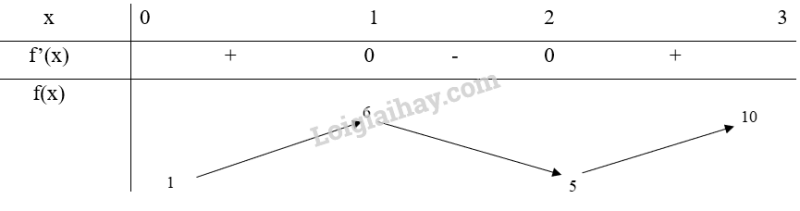
Từ bảng biến thiên, ta thấy và
b) Xét trên khoảng (0;5)
Bảng biến thiên:
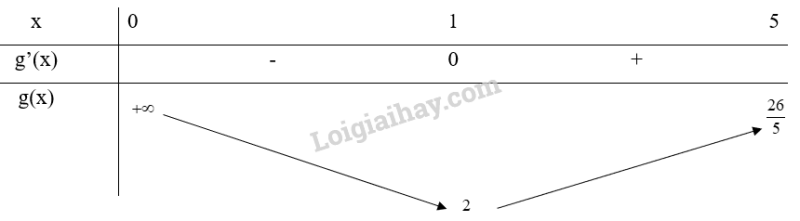
Từ bảng biến thiên, ta thấy và hàm số không tồn tại giá trị lớn nhất trên khoảng (0;5)
c) Xét
Tập xác định:
Tập xác định mới:
Bảng biến thiên:
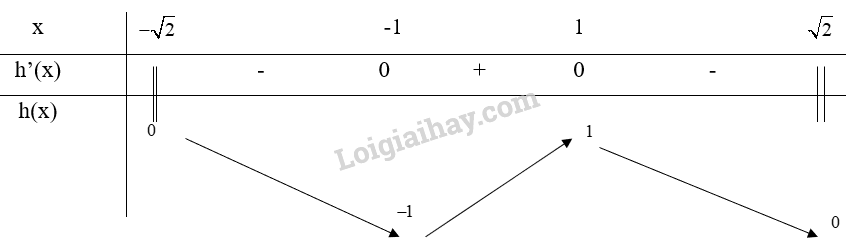
Từ bảng biến thiên, ta thấy và
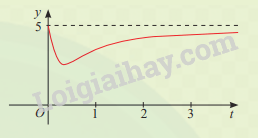
Sự phân huỷ của rác thải hữu cơ có trong nước sẽ làm tiêu hao oxygen hoà tan trong nước. Nồng độ oxygen (mg/l) trong một hồ nước sau t giờ (t 0) khi một lượng rác thải hữu cơ bị xả vào hồ được xấp xỉ bởi hàm số (có đồ thị như đường màu đỏ ở hình bên)
Vào các thời điểm nào nồng độ oxygen trong nước cao nhất và thấp nhất?
(Theo: https://www.researchgate.net/publication/264903978_Microrespirometric_ characterization _of_activated_sludge_inhibition_by_copper_and_zinc)
Lời giải:
Xét trên nửa đoạn
Bảng biến thiên:
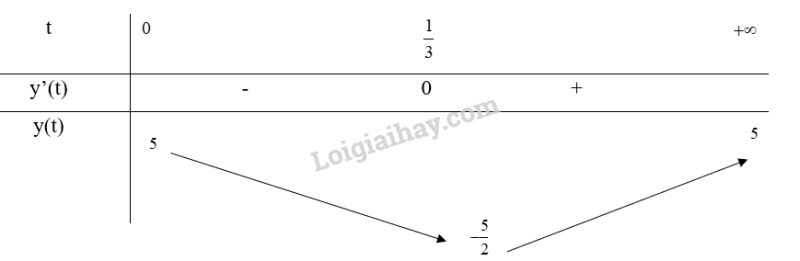
Từ bảng biến thiên, ta thấy và
Vậy vào các thời điểm t = 0 thì nồng độ oxygen trong nước cao nhất và t = giờ thì nồng độ oxygen trong nước thấp nhất
2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn
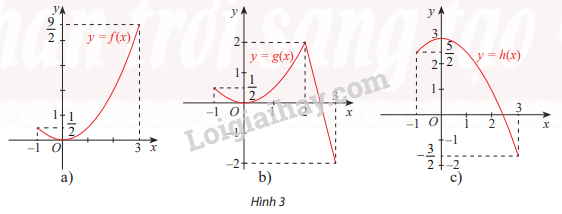
Hoạt động khám phá 2 trang 16 Toán 12 Tập 1: Hình 3 cho ta đồ thị của ba hàm số
; và trên đoạn [-1;3]
a) Hàm số nào đạt giá trị lớn nhất tại một điểm cực đại của nó?
b) Các hàm số còn lại đạt giá trị lớn nhất tại điểm nào?
Lời giải:
a) đạt giá trị cực đại tại x = 0 và
b) và
Lời giải:
Xét trên đoạn [1;4]
Bảng biến thiên:
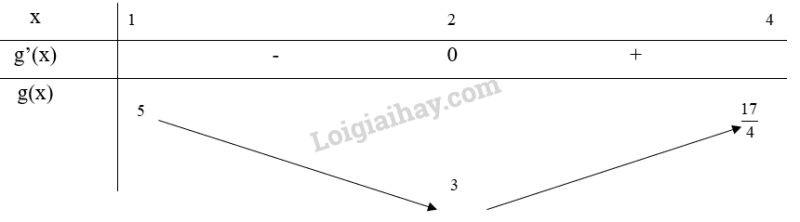
Từ bảng biến thiên, ta thấy và
Lời giải:
Đặt một cạnh góc vuông là x (x > 0) thì cạnh còn lại là
Diện tích tam giác vuông là:
Tập xác định:
Tập xác định mới:
Bảng biến thiên:
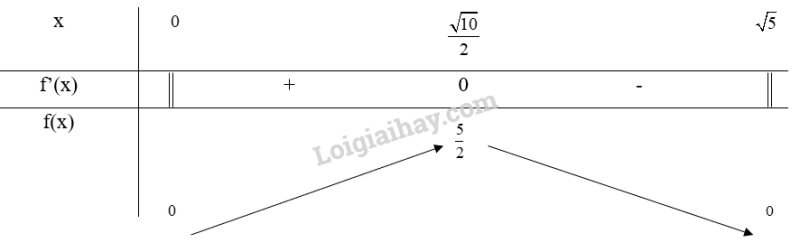
Từ bảng biến thiên, ta thấy
Vậy diện tích lớn nhất của tam giác là
Bài tập
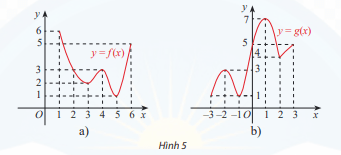
Lời giải:
a) Từ đồ thị, ta thấy và
b) Từ đồ thị, ta thấy và
Bài 2 trang 18 Toán 12 Tập 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) trên đoạn [-1;3]
b) trên đoạn [3;11]
c) trên đoạn [3;7]
d) trên đoạn
Lời giải:
a) Xét trên đoạn [-1;3]
Bảng biến thiên:
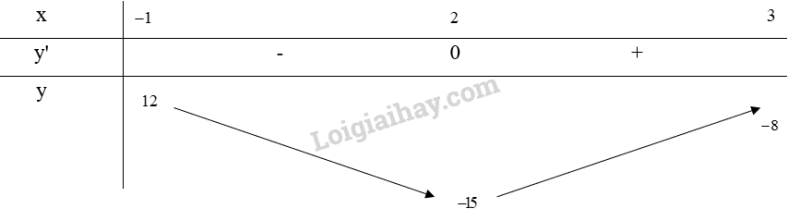
Từ bảng biến thiên, ta thấy và
b) Xét trên đoạn [3;11]
Bảng biến thiên:
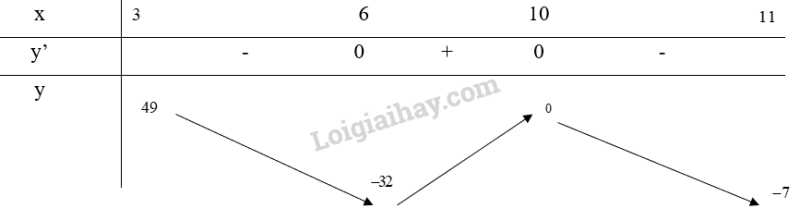
Từ bảng biến thiên, ta thấy và
c) Xét trên đoạn [3;7]
Bảng biến thiên:
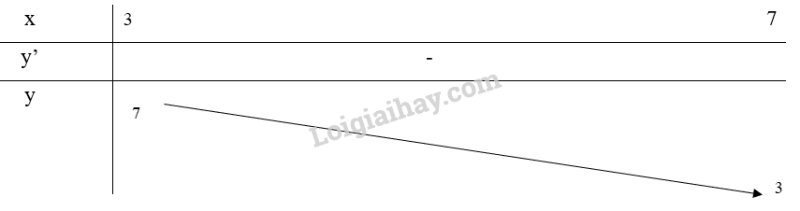
Từ bảng biến thiên, ta thấy và
d) Xét trên đoạn
Ta có:
Bảng biến thiên:
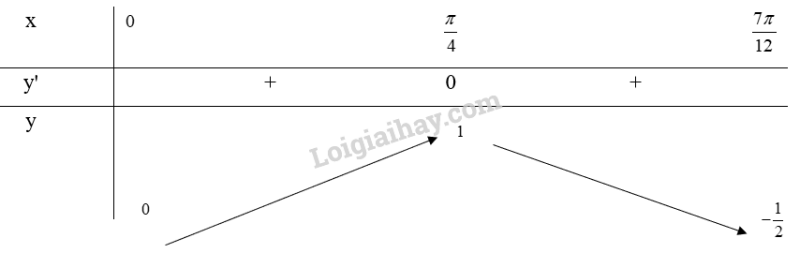
Từ bảng biến thiên, ta thấy và
Bài 3 trang 18 Toán 12 Tập 1: Tìm giá trị nhỏ nhất của các hàm số sau:
a) trên nửa khoảng [-3;2)
b) trên khoảng
Lời giải:
a) Xét trên nửa khoảng [-3;2)
Bảng biến thiên:
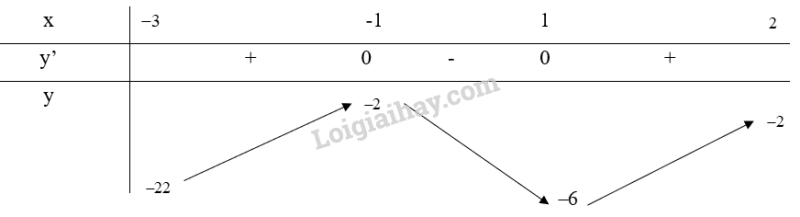
Từ bảng biến thiên, ta thấy
b) Xét trên khoảng
Tập xác định:
Bảng biến thiên:
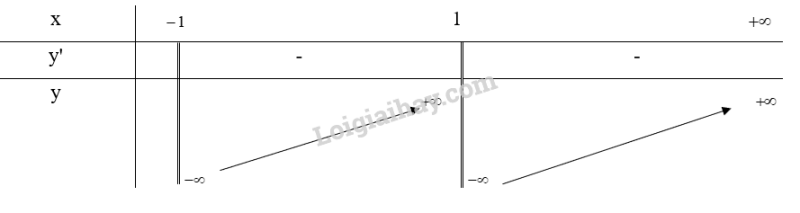
Từ bảng biến thiên, ta thấy hàm số không tồn tại giá trị nhỏ nhất trên khoảng

Lời giải:
Gọi a, b lần lượt là chiều dài và chiều rộng của cửa sổ (m; a,b > 0)
Chu vi cửa sổ là:
Diện tích cửa sổ là:
Bảng biến thiên:
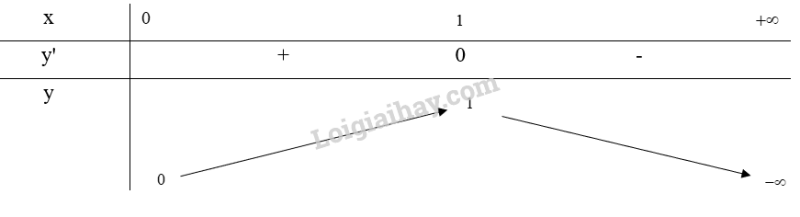
Từ bảng biến thiên, ta thấy
Vậy để diện tích cửa sổ lớn nhất bằng thì chiều dài và chiều rộng bằng nhau và bằng 1m
Bài 5 trang 18 Toán 12 Tập 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Lời giải:
Tập xác định:
Tập xác định mới:
Bảng biến thiên:
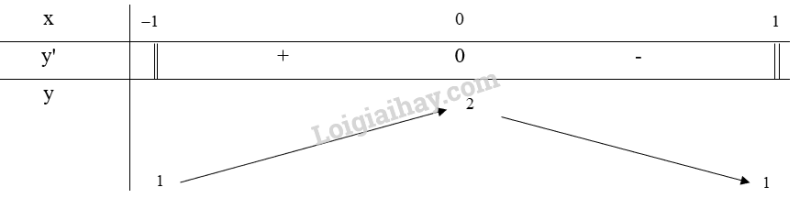
Từ bảng biến thiên, ta thấy và
a) Viết công thức biểu diễn theo .
b) Tìm giá bán mỗi kilôgam sản phẩm để đạt được doanh thu cao nhất và xác định doanh thu cao nhất đó.
Lời giải:
a) Ta có:
Thay vào ta được:
b) Đặt
Tập xác định:
Bảng biến thiên:
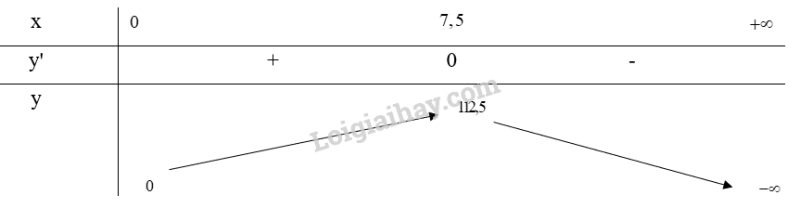
Từ bảng biến thiên, ta thấy
Vậy nếu giá bán mỗi kilôgam sản phẩm là 7,5 nghìn đồng/kg thì sẽ đạt được doanh thu cao nhất là 112,5 nghìn đồng
Lời giải:
Gọi chiều cao của hộp là h (cm)
Thể tích của hộp là:
Diện tích toàn phần của hộp là:
Tập xác định:
Bảng biến thiên:
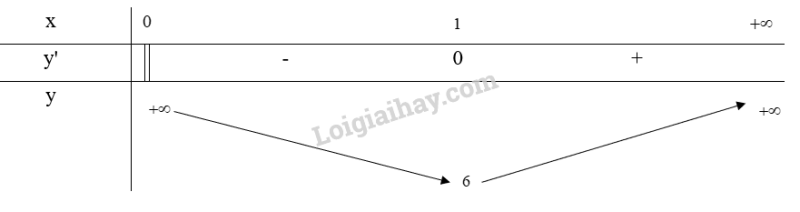
Từ bảng biến thiên, ta thấy
Vậy x = 1cm thì diện tích toàn phần của hộp nhỏ nhất và bằng 6
Xem thêm các bài giải bài tập Toán lớp 12 Chân trời sáng tạo hay, chi tiết khác:
Bài 1. Tính đơn diệu và cực trị của hàm số
Bài 2. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Bài 3. Đường tiệm cận của đồ thị hàm số
Bài 4. Khảo sát và vẽ đồ thị một số hàm số cơ bản
Bài 1. Vectơ và các phép toán trong không gian
Lý thuyết Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
1. Định nghĩa Khái niệm GTLN, GTNN của hàm số
|
Cho hàm số y = f(x) xác định trên tập D.
Kí hiệu M = hoặc M =
|
2. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn
|
Các bước tìm GTLN và GTNN của hàm số f(x) trên đoạn :
|
Ví dụ: Tìm GTLN và GTNN của hàm số trên đoạn
Ta có: hoặc (vì )
y(0) = 3; y(4) = 195; y() = -1
Do đó: ;