Tài liệu chuyên đề Đại số tổ hợpToán lớp 10 sách Kết nối tri thức gồm lý thuyết và các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Toán 10. 

Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Toán 10 Kết nối tri thức word có lời giải chi tiết:

B1: Gửi phí vào tài khoản0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây

Xem thử tài liệu tại đây: Link tài liệu

Chuyên đề Đại số tổ hợp

Tài liệu gồm 4 Chuyên đề nhỏ, mời bạn đọc xem thử nội dung Chuyên đề Hoán vị. chỉnh hợp và tổ hợp :

Chuyên đề 2: HOÁN VỊ, CHỈNH HỢP VÀ TỔ HỢP

Câu 1:         Tính số chỉnh hợp chập \[4\] của \[7\] phần tử?

A. \[24\].                          B. \[720\].                      C. \[840\].                      D. \[35\].

Lời giải

Ta có: \[A_7^4 = \frac{{7!}}{{3!}} = 840\].

Câu 2:         Công thức tính số chỉnh hợp chập \(k\) của \(n\) phần tử là:

A. \(A_n^k = \frac{{n!}}{{\left( {n - k} \right)!}}.\) B. \(A_n^k = \frac{{n!}}{{\left( {n - k} \right)!k!}}.\)                  C. \(C_n^k = \frac{{n!}}{{\left( {n - k} \right)!k!}}.\)                  D. \(C_n^k = \frac{{n!}}{{\left( {n - k} \right)!}}.\)

Lời giải

Câu hỏi lí thuyết.

Câu 3:         Công thức tính số tổ hợp chập \(k\) của \(n\) phần tử là:

A. \(A_n^k = \frac{{n!}}{{\left( {n - k} \right)!}}.\) B. \(A_n^k = \frac{{n!}}{{\left( {n - k} \right)!k!}}.\)                  C. \(C_n^k = \frac{{n!}}{{\left( {n - k} \right)!k!}}.\)                  D. \(C_n^k = \frac{{n!}}{{\left( {n - k} \right)!}}.\)

Lời giải

Câu hỏi lí thuyết.

Câu 4:         Mệnh đề nào đúng trong các mệnh đề sau:

Lời giải

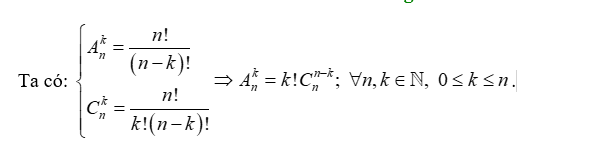
Câu 5:         Cho ,  là các số nguyên dương. Mệnh đề nào sau đây sai?

Lời giải

Theo định nghĩa về tổ hợp, chỉnh hợp và hoán vị,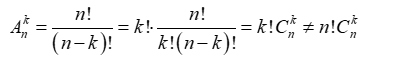 

Câu 6:         Có bao nhiêu số có ba chữ số dạng \[\overline {abc} \] với \(a,\;b,\;c \in \left\{ {0;\;1;2;\;3;\;4;\;5;\;6} \right\}\) sao cho \(a < b < c\).

A. \(30\).                          B. \(20\).                        C. \(120\).                      D. \(40\).

Lời giải

Chọn B

Nhận xét \(a,\;b,\;c \in \left\{ {0;\;1;2;\;3;\;4;\;5;\;6} \right\}\)

Số các số tự nhiên thỏa mãn bài ra bằng số các tổ hợp chập \(3\) của \(6\) phần tử thuộc tập hợp

\(\left\{ {1,2,3,4,5,6} \right\}\).

Vậy có \(C_6^3 = 20\) số.

Câu 7:         Có n phần tử lấy ra k phần tử đem đi sắp xếp theo một thứ tự nào đó,mà khi thay đổi thứ tự ta được cách sắp xếp mới. Khi đó số cách sắp xếp là:

Lời giải

Do mỗi cách lấy k trong n phần thử rồi sắp thứ tự ta được một chỉnh hợp chập k của n phần tử nên tất cả các chỉnh hợp là 

Câu 8:         Từ các chữ số \[1\]; \[2\]; \[3\]; \[4\] có thể lập được bao nhiêu số tự nhiên có \[4\] chữ số đôi một khác nhau?

A. \(12\).                          B. \(24\).                        C. \(42\).                        D. \({4^4}\).

Lời giải

Mỗi số tự nhiên có \[4\] chữ số đôi một khác nhau được tạo thành từ các chữ số \[1\]; \[2\]; \[3\]; \[4\] là một hoán vị của \[4\] phần tử. Vậy số các số cần tìm là: \[4! = 24\] số.

Câu 9:         Cho tập hợp \(M\) có \(10\) phần tử. Số tập con gồm \(2\) phần tử của \(M\) là

A. \(A_{10}^8\).               B. \(A_{10}^2\).             C. \(C_{10}^2\).             D. \({10^2}\).

Lời giải

Số tập con gồm \(2\) phần tử của \(M\) là số cách chọn \(2\) phần tử bất kì trong \(10\) phần tử của \(M\). Do đó số tập con gồm \(2\) phần tử của \(M\) là \(C_{10}^2\).

Câu 10:      Có bao nhiêu cách sắp xếp \(5\) học sinh thành một hàng dọc?

A. \({5^5}\).                     B. \(5!\).                         C. \(4!\).                         D. \(5\).

Lời giải

Số cách sắp xếp \(5\) học sinh thành một hàng dọc là \(5!\).

Câu 11:      Cho \(A = \left\{ {1,\,2,\,3,\,4} \right\}\). Từ \(A\) lập được bao nhiêu số tự nhiên có \(4\) chữ số đôi một khác nhau?

A. \(32\).                          B. \(24\).                        C. \(256\).                      D. \(1\).

Lời giải

Mỗi số tự nhiên tự nhiên có \(4\) chữ số khác nhau được lập từ tập \(A\) là hoán vị của \(4\) phần tử.

Vậy có \(4! = 24\) số cần tìm.

Câu 12:      Từ các số \(1\), \[2\], \(3\), \(4\), \[5\] có thể lập được bao nhiêu số tự nhiên có \(5\) chữ số khác nhau đôi một?

A. \(60\).                          B. \(120\).                      C. \(24\).                        D. \(48\).

Lời giải

Mỗi cách lập số tự nhiên có 5 chữ số khác nhau đôi một hoán vị của 5 phần tử.

Vậy có \(5! = 120\)số cần tìm.

Câu 13:      Từ tập \(X = \left\{ {2,3,4,5,6} \right\}\) có thể lập được bao nhiêu số tự nhiên có ba chữ số mà các chữ số đôi một khác nhau?

A. \(60\).                          B. \(125\).                      C. \(10\).                        D. \(6\).

Lời giải

Số các số tự nhiên có ba chữ số mà các chữ số đôi một khác nhau được lập từ tập \(X\) là số chỉnh hợp chập \(3\) của \(5\) phần tử\( \Rightarrow \) số các số cần lập là \(A_5^3 = 60\).

Câu 14:      Nhân dịp lễ sơ kết học kì I, để thưởng cho ba học sinh có thành tích tốt nhất lớp cô An đã mua \(10\) cuốn sách khác nhau và chọn ngẫu nhiên ra \(3\) cuốn để phát thưởng cho \(3\) học sinh đó mỗi học sinh nhận \(1\) cuốn. Hỏi cô An có bao nhiêu cách phát thưởng.

A. \[C_{10}^3\].               B. \[A_{10}^3\].             C. \[{10^3}\].                 D. \[3.C_{10}^3\].

Lời giải

Chọn ngẫu nhiên \(3\) cuốn sách rồi phát cho \(3\) học sinh có: \[A_{10}^3\] cách.

Câu 15:      Cần chọn \(3\) người đi công tác từ một tổ có \(30\) người, khi đó số cách chọn là

A. \(A_{30}^3\).               B. \({3^{30}}\).             C. \(10\).                        D. \(C_{30}^3\).

Lời giải

Số cách chọn \(3\) người bất kì trong \(30\) là: \(C_{30}^3\).

Câu 16:      Số véctơ khác \[\overrightarrow 0 \] có điểm đầu, điểm cuối là hai trong \(6\) đỉnh của lục giác \[ABCDEF\] là

A. \[{P_6}.\]                     B. \[C_6^2.\]                  C. \[A_6^2.\]                  D. \[36.\]

Lời giải

Số véc-tơ khác \[\overrightarrow 0 \] có điểm đầu, điểm cuối là hai trong \(6\) đỉnh của lục giác \[ABCDEF\] là\(A_6^2\).

Câu 17:      Số tập hợp con có \[3\] phần tử của một tập hợp có \[7\] phần tử là

A. \[A_7^3\].                    B. \[C_7^3\].                  C. \[7\].                          D. \[\frac{{7!}}{{3!}}\].

Lời giải

Chọn ba phần tử trong tập hợp bẩy phần tử để tạo thành một tập hợp mới là tổ hợp chập ba của bẩy phần tử \(C_7^3\).

Câu 18:      Số hoán vị của \(n\) phần tử là

A. \[n!\].                           B. \[2n\].                        C. \[{n^2}\].                   D. \[{n^n}\].

Lời giải

Sô hoán vị của tập có \(n\) phần tử bằng \(n!\).

Câu 19:      Tập \[A\] gồm \(n\) phần tử \(\left( {n > 0} \right)\). Hỏi \[A\] có bao nhiêu tập con?

A. \[A_n^2\].                    B. \[C_n^2\].                  C. \[{2^n}\].                   D. \({3^n}\).

Lời giải

Số tập con gồm \(k\) phần tử của tập \[A\] là \(C_n^k\).

Số tất cả các tập con của tập \(A\) là 

Câu 20:      Có bao nhiêu số tự nhiên có \[5\] chữ số, các chữ số khác \[0\] và đôi một khác nhau?

A. \(5!\).                           B. \({9^5}\).                   C. \(C_9^5\).                  D. \(A_9^5\).

Lời giải

Mỗi số tự nhiên có \[5\] chữ số, các chữ số khác \[0\] và đôi một khác nhau là một chỉnh hợp chập \[5\] của \[9\] phần tử.

Vậy số các số tự nhiên thỏa đề bài là \(A_9^5\) số.

Câu 21:      Trong một buổi khiêu vũ có \(20\) nam và \(18\) nữ. Hỏi có bao nhiêu cách chọn ra một đôi nam nữ để khiêu vũ?

A. \(C_{38}^2\).               B. \(A_{38}^2\).             C. \(C_{20}^2C_{18}^1\).                                        D. \(C_{20}^1C_{18}^1\).

Lời giải

Chọn một nam trong \(20\) nam có \(C_{20}^1\) cách.

Chọn một nữ trong \(18\) nữ có \(C_{18}^1\) cách.

Theo quy tắc nhân, số cách chọn một đôi nam nữ là \(C_{20}^1C_{18}^1\).

Câu 22:      Cho tập hợp \(A\) có \(20\) phần tử, số tập con có hai phần tử của \(A\) là

A. \(2C_{20}^2\).             B. \(2A_{20}^2\).           C. \(C_{20}^2\).             D. \(A_{20}^2\).

Lời giải

Số tập con có hai phần tử của \(A\) là \(C_{20}^2\).

Câu 23:      Có bao nhiêu cách chọn \(5\) cầu thủ từ \(11\) trong một đội bóng để thực hiện đá \(5\) quả luân lưu \(11{\rm{ m}}\), theo thứ tự quả thứ nhất đến quả thứ năm.

A. \(A_{11}^5\).               B. \(C_{11}^5\).             C. \(A_{11}^2.5!\).         D. \(C_{10}^5\).

Lời giải

Số cách chọn \(5\) cầu thủ từ \(11\) trong một đội bóng để thực hiện đá \(5\) quả luân lưu \(11{\rm{ m}}\), theo thứ tự quả thứ nhất đến quả thứ năm là số chỉnh hợp chập \(5\) của \(11\) phần tử nên số cách chọn là \(A_{11}^5\).

Câu 24:      Cho \(8\) điểm trong đó không có \(3\) điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác mà ba đỉnh của nó được chọn từ \(8\) điểm trên?

A. \(336\).                         B. \(56\).                        C. \(168\).                      D. \(84\).

Lời giải

Có \(C_8^3 = 56\) tam giác.

Câu 25:      Một hộp đựng hai viên bi màu vàng và ba viên bi màu đỏ. Có bao nhiêu cách lấy ra hai viên bi trong hộp?

A. \(10\).                          B. \(20\).                        C. \(5\).                          D. \(6\).

Lời giải

Số cách lấy ra hai viên bi là \(C_5^2 = 10\).

Câu 26:      Số giao điểm tối đa của \(10\) đường thẳng phân biệt là

A. \(50\).                          B. \(100\).                      C. \(120\).                      D. \(45\).

Lời giải

Số giao điểm tối đa của \(10\) đường thẳng phân biệt là \(C_{10}^2 = 45\).

Câu 27:      Cho tập hợp \(S\) có \[10\] phần tử. Tìm số tập con gồm \[3\] phần tử của \(S\).

A. \(A_{10}^3\).               B. \(C_{10}^3\).             C. \(30\).                        D. \({10^3}\).

Lời giải

Số tập con gồm \[3\] phần tử được lấy ra từ tập hợp gồm \[10\] phần tử ban đầu là tổ hợp chập \[3\] của \[10\]. Đáp án \(C_{10}^3\).

Câu 28:      Trong trận chung kết bóng đá phải phân định thắng thua bằng đá luân lưu \[11\] mét. Huấn luyện viên của mỗi đội cần trình với trọng tài một danh sách sắp thứ tự \[5\] cầu thủ trong \[11\] cầu thủ để đá luân lưu \[5\] quả \[11\] mét. Hỏi huấn luyện viên của mỗi đội sẽ có bao nhiêu cách chọn?

A. \(55440\).                     B. \(120\).                      C. \(462\).                      D. \(39916800\).

Lời giải

Số cách chọn của huấn luyện viên của mỗi đội là \[A_{11}^5 = 55440\].

Câu 29:      Cho tập hợp \(S = \left\{ {1;2;3;4;5;6} \right\}\). Có thể lập được bao nhiêu số tự nhiên gồm bốn chữ số khác nhau lấy từ tập hợp \(S\)?

A. \(360\).                         B. \(120\).                      C. \(15\).                        D. \(20\).

Lời giải

Từ tập \(S\) lập được \(A_6^4 = 360\) số tự nhiên gồm bốn chữ số khác nhau.

Câu 30:      Cần phân công ba bạn từ một tổ có \[10\] bạn để làm trực nhật. Hỏi có bao nhiêu cách phân công khác nhau?

A. \(720\).                         B. \({10^3}\).                 C. \(120\).                      D. \(210\).

Lời giải

Số cách phân công là \(C_{10}^3 = 120\).

Câu 31:      Cho tập \(M = \left\{ {1;2;3;4;5;6;7;8;9} \right\}\). Số các số tự nhiên gồm \(4\) chữ số phân biệt lập từ \(M\) là.

A. \(4!\).                           B. \(A_9^4\).                  C. \({4^9}\).                   D. \(C_9^4\).

Lời giải

Số các số tự nhiên gồm \(4\) chữ số phân biệt lập từ \(M\) là \(A_9^4\).

Câu 32:      Số cách chọn \(3\) học sinh từ \(5\) học sinh là

A. \(C_5^3\).                     B. \(A_5^3\).                  C. \(3!\).                         D. \(15\).

Lời giải

Số cách chọn \(3\) học sinh từ \(5\) học sinh là \(C_5^3\).

Câu 33:      Một tổ có \[10\] học sinh. Hỏi có bao nhiêu cách chọn ra \[2\] học sinh từ tổ đó để giữ hai chức vụ tổ trưởng và tổ phó.

A. \[A_{10}^2\].               B. \[C_{10}^2\].             C. \[A_{10}^8\].             D. \[{10^2}\].

Lời giải

Chọn ra \[2\] học sinh từ một tổ có \[10\] học sinh và phân công giữ chức vụ tổ trưởng, tổ phó là một chỉnh hợp chập \[2\] của 10 phần tử. Số cách chọn là \[A_{10}^2\] cách.

Câu 34:      Trong mặt phẳng cho \(15\) điểm phân biệt trong đó không có \(3\) điểm nào thẳng hàng. Số tam giác có đỉnh là \(3\) trong số \(15\) điểm đã cho là.

A. \(A_{15}^3\).               B. \(15!\).                       C. \(C_{15}^3\).             D. \({15^3}\).

Lời giải

Số tam giác có đỉnh là \(3\) trong số \(15\) điểm đã cho là: \(C_{15}^3\).

Câu 35:      Số cách chọn \(5\) học sinh trong một lớp có \(25\) học sinh nam và \(16\) học sinh nữ là

A. \[C_{25}^5 + C_{16}^5\].                                  B. \[C_{25}^5\].             C. \[A_{41}^5\].                    D. \[C_{41}^5\].

Lời giải

Chọn \[5\] học sinh trong lớp có \[41\] học sinh là số tập con có \[5\] phần tử chọn trong \[41\] phần tử nên số cách chọn là \[C_{41}^5\].

Câu 36:      Một nhóm học sinh có \(10\) người. Cần chọn \(3\) học sinh trong nhóm để làm \(3\) công việc là tưới cây, lau bàn và nhặt rác, mỗi người làm một công việc. Số cách chọn là

A. \({10^3}\).                   B. \(3 \times 10\).           C. \(C_{10}^3\).             D. \(A_{10}^3\).

Lời giải

Số cách chọn \(3\) em học sinh là số cách chọn \(3\) phần tử khác nhau trong \(10\) phần tử có phân biệt thứ tự nên số cách chọn thỏa yêu cầu là \(A_{10}^3\).

Câu 37:      Cho tập hợp \(M = \left\{ {0;\,\,1;\,\,2;\,\,3;\,\,4;\,\,5;\,\,6;\,\,7;\,\,8;\,\,9} \right\}\) có \(10\) phần tử. Số tập hợp con gồm \(2\) phần tử của \(M\) và không chứa phần tử \(1\) là

A. \[C_{10}^2\].               B. \[A_9^2\].                  C. \[{9^2}\].                   D. \[C_9^2\].

Lời giải

Câu 38:      Từ tập \(A = \left\{ {1;2;3;4;5;6;7} \right\}\) có thể lập được bao nhiêu số tự nhiên có \(5\) chữ số đôi một khác nhau

A. \(5!\).                           B. \(C_7^5\).                  C. \(A_7^5\).                  D. \({7^5}\).

Lời giải

Số tự nhiên có \(5\) chữ số đôi một khác nhau có thể lập được là: \(A_7^5\) số.

Câu 39:      Cho \[A\] là tập hợp gồm \[20\] điểm phân biệt. Số đoạn thẳng có hai đầu mút phân biệt thuộc tập \[A\] là

A. \(170\).                         B. \(160\).                      C. \(190\).                      D. \(360\).

Lời giải

Số đoạn thẳng là \[C_{20}^2 = 190\].