Tài liệu chuyên đề Phương pháp tọa độ trong mặt phẳng Toán lớp 10 sách Kết nối tri thức gồm lý thuyết và các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Toán 10. 

Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Toán 10 Kết nối tri thức word có lời giải chi tiết:

B1: Gửi phí vào tài khoản0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây

Xem thử tài liệu tại đây: Link tài liệu

Chuyên đề Phương pháp tọa độ trong mặt phẳng

Tài liệu gồm 4 Chuyên đề nhỏ, mời bạn đọc xem thử nội dung Chuyên đề Vị trí tương đối của hai đường thẳng. Góc và khoảng cách :

Chuyên đề 2: VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG. GÓC VÀ KHOẢNG CÁCH

DẠNG 1. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG

Câu 1:           Có bao nhiêu cặp đường thẳng song song trong các đường thẳng sau?

\[\left( {{d_1}} \right):\,y\, = \, - \frac{1}{{\sqrt 2 }}x - 2;\] \[\left( {{d_2}} \right):\,y\, = \, - \frac{1}{2}x + 3;\] \[\left( {{d_3}} \right):\,y\, = \,\frac{1}{2}x + 3;\] \[\left( {{d_4}} \right):\,y\, = \, - \frac{{\sqrt 2 }}{2}x - 2\]

A. \[3\].                            B. \[2\].                          C. \[1\].                          D. \[0\].

Lời giải

Chọn D

Hai đường thẳng \[y\, = \,{a_1}x + {b_1}\] và \[y\, = \,{a_2}x + {b_2}\] song song với nhau khi và chỉ khi \[\left\{ \begin{array}{l}{a_1}\, = \,{a_2}\\{b_1}\, \ne \,{b_2}\end{array} \right..\]

Trong các đường thẳng trên không có đường nào thỏa mãn. Vậy không có cặp đường thẳng nào song song.

Câu 2:         Phương trình nào sau đây là phương trình đường thẳng không song song với đường thẳng \[d:y = 3x - 2\]

A. \[ - 3x + y = 0\].          B. \[3x - y - 6 = 0\].       C. \[3x - y + 6 = 0\].      D. \[3x + y - 6 = 0\].

Lời giải

Chọn D

\[d:y = 3x - 2 \Leftrightarrow 3x - y - 2 = 0\]. \[\left( d \right)\] có VTPT \[\overrightarrow n  = \left( {3; - 1} \right)\].

Đường thẳng \[3x + y - 6 = 0\] có VTPT \[\overrightarrow {{n_1}}  = \left( {3;1} \right) \ne k\overrightarrow n \] nên \[\overrightarrow n \] và \[\overrightarrow {{n_1}} \] không cùng phương. Do đó đường thẳng \[3x + y - 6 = 0\] không song song với đường thẳng \[\left( d \right)\].

Câu 3:         Trong mặt phẳng \[Oxy\], đường thẳng \[d:\,x - 2y - 1 = 0\] song song với đường thẳng có phương trình nào sau đây?

A. \[x + 2y + 1 = 0\].       B. \[2x - y = 0\].            C. \[ - x + 2y + 1 = 0\].  D. \[ - 2x + 4y - 1 = 0\].

Lời giải

Chọn D

Ta kiểm tra lần lượt các đường thẳng

.+) Với \[d{}_1:x + 2y + 1 = 0\] có \[\frac{1}{1} \ne \frac{2}{{ - 2}} \Rightarrow d\] cắt \[d{}_1\].

.+) Với \[d{}_2:2x - y = 0\] có \[\frac{2}{1} \ne \frac{{ - 1}}{{ - 2}} \Rightarrow d\]cắt \[d{}_2\].

.+) Với \[d{}_3: - x + 2y + 1 = 0\] có \[\frac{{ - 1}}{1} = \frac{2}{{ - 2}} \ne \frac{1}{{ - 1}} \Rightarrow d\]trùng \[d{}_3\].

.+) Với \[d{}_4: - 2x + 4y - 1 = 0\] có \[\frac{1}{{ - 2}} = \frac{{ - 2}}{4} \ne \frac{{ - 1}}{{ - 1}} \Rightarrow d\] song song \[d{}_4\].

Câu 4:         Cho các đường thẳng sau.

\({d_1}:y = \frac{3}{{\sqrt 3 }}x - 2\) \({d_2}:y = \frac{1}{{\sqrt 3 }}x + 1\) \({d_3}:y =  - \left( {1 - \frac{{\sqrt 3 }}{3}} \right)x + 2\) \({d_4}:y = \frac{{\sqrt 3 }}{3}x - 1\)

Khẳng định nào đúng trong các khẳng định sau?

A. \({d_2},{d_3},{d_4}\)song song với nhau.      B. \({d_2}\) và \({d_4}\)song song với nhau.

C. \({d_1}\)và \({d_4}\)vuông góc với nhau.        D. \({d_2}\) và \({d_3}\)song song với nhau.

Lời giải

Chọn B

Vì \({d_3}:y =  - \left( {1 - \frac{{\sqrt 3 }}{3}} \right)x + 2 = \frac{1}{{\sqrt 3 }}x + 1 \Rightarrow {d_3} \equiv {d_2}\). Đường thẳng \({d_2}\) và \({d_4}\)có hệ số góc bằng nhau;hệ số tự do khác nhau nên chúng song song.

Câu 5:         Tìm các giá trị thực của tham số \(m\) để đường thẳng \(y = \left( {{m^2} - 3} \right)x + 3m + 1\) song song với đường thẳng \(y = x - 5\).

A. \[m =  \pm 2\].            B. \[m =  \pm \sqrt 2 \].                                     C. \[m =  - 2\].                      D. \[m = 2\].

Lời giải

Chọn D

Để đường thẳng \(y = \left( {{m^2} - 3} \right)x + 3m + 1\) song song với đường thẳng \(y = x - 5\) thì điều kiện là

\(\left\{ \begin{array}{l}{m^2} - 3 = 1\\3m + 1 \ne  - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m =  \pm 2\\m \ne  - 2\end{array} \right. \Leftrightarrow m = 2\).

Câu 6:         Tọa độ giao điểm của hai đường thẳng \(x - 3y - 6 = 0\) và \(3x + 4y - 1 = 0\) là

A. \(\left( {\frac{{27}}{{13}}; - \frac{{17}}{{13}}} \right)\).                       B. \(\left( { - 27;17} \right)\).                                     C. \(\left( { - \frac{{27}}{{13}};\frac{{17}}{{13}}} \right)\).      D. \(\left( {27; - 17} \right)\).

Lời giải

Chọn A

Ta có tọa độ giao điểm của hai đường thẳng \(x - 3y - 6 = 0\) và \(3x + 4y - 1 = 0\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - 3y - 6 = 0\\3x + 4y - 1 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{27}}{{13}}\\y =  - \frac{{17}}{3}\end{array} \right.\).

Câu 7:         Cho đường thẳng \[{d_1}:2x + 3y + 15 = 0\] và \[{d_2}:x - 2y - 3 = 0\]. Khẳng định nào sau đây đúng?

A. \({d_1}\) và \({d_2}\) cắt nhau và không vuông góc với nhau.            

B. \({d_1}\) và \({d_2}\) song song với nhau.

C. \({d_1}\) và \({d_2}\) trùng nhau.                    

D. \({d_1}\) và \({d_2}\) vuông góc với nhau.

Lời giải

Chọn A

Đường thẳng\[{d_1}:2x + 3y + 15 = 0\] có một vectơ pháp tuyến là \[\overrightarrow {{n_1}}  = \left( {2;3} \right)\] và đường thẳng \[{d_2}:x - 2y - 3 = 0\] có một vectơ pháp tuyến là \[\overrightarrow {{n_2}}  = \left( {1; - 2} \right)\].

Ta thấy \[\frac{2}{1} \ne \frac{3}{{ - 2}}\] và \[\overrightarrow {{n_1}} .\overrightarrow {{n_2}}  = 2.1 + 3.( - 2) =  - 4 \ne 0\].

Vậy \({d_1}\) và \({d_2}\) cắt nhau và không vuông góc với nhau.

Câu 8:         Hai đường thẳng \({d_1}:\,mx + y = m - 5,\,{d_2}:\,x + my = 9\) cắt nhau khi và chỉ khi

A. \[m \ne  - 1\].              B. \[m \ne 1\].               C. \[m \ne  \pm 1\].       D. \[m \ne 2\].

Lời giải

Chọn C

CÁCH 1

-Xét \(m = 0\) thì \({d_1}:\,y =  - 5,\,{\rm{ }}{d_2}:\,x = 9\). Rõ ràng hai đường thẳng này cắt nhau nên \(m = 0\) thỏa

mãn .

-Xét \(m \ne 0\) thì \({d_1}:\,y =  - mx + m - 5\) và \({d_2}:\,y =  - \frac{x}{m} + 9\)

Hai đường thẳng \({d_1}\) và \({d_2}\) cắt nhaut\( \Leftrightarrow  - m \ne  - \frac{1}{m} \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne  \pm 1\end{array} \right.{\rm{ (2)}}\).

Từ  và  ta có \(m \ne  \pm 1\).

CÁCH 2

\({d_1}\) và \({d_2}\) theo thứ tự nhận các vectơ \({\vec n_1} = (m;1),{\rm{ }}{\vec n_2} = (1;m)\) làm vec tơ pháp tuyến.

\({d_1}\) và \({d_2}\) cắt nhau \( \Leftrightarrow {\vec n_1}\) và \({\vec n_2}\) không cùng phương \( \Leftrightarrow \)\(m.m \ne 1.1 \Leftrightarrow m \ne  \pm 1.\)

Câu 9:         Với giá trị nào của \[m\] thì hai đường thẳng

\[{d_1}:3x + 4y + 10 = 0\] và \[{d_2}:\left( {2m - 1} \right)x + {m^2}y + 10 = 0\] trùng nhau?

A. \(m \pm 2\).                B. \[m =  \pm 1\].         C. \[m = 2\].                  D. \(m =  - 2\).

Lời giải

Câu 10:      Trong mặt phẳng với hệ tọa độ \[Oxy\], cho hai đường thẳng có phương trình \[{d_1}:mx + \left( {m - 1} \right)y + 2m = 0\] và \[{d_2}:2x + y - 1 = 0\]. Nếu \[{d_1}\] song song \[{d_2}\] thì:

A. \[m = 2.\]                     B. \[m =  - 1.\]               C. \[m =  - 2.\]               D. \[m = 1.\]

Lời giải

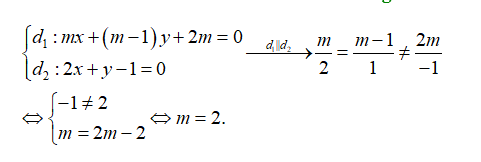
Câu 11:      Tìm \(m\) để hai đường thẳng \[{d_1}:2x - 3y + 4 = 0\] và \[{d_2}:\left\{ \begin{array}{l}x = 2 - 3t\\y = 1 - 4mt\end{array} \right.\] cắt nhau.

A. \(m \ne  - \frac{1}{2}.\)                                     B. \(m \ne 2.\)               C. \(m \ne \frac{1}{2}.\)       D. \(m = \frac{1}{2}.\)

Lời giải

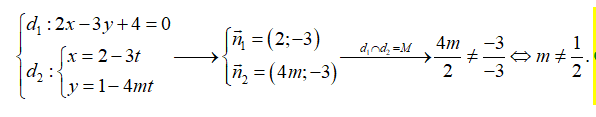
Chọn C

Câu 12:      Với giá trị nào của \(a\) thì hai đường thẳng

\[{d_1}:2x--4y + 1 = 0\] và \({d_2}:\left\{ \begin{array}{l}x =  - 1 + at\\y = 3 - \left( {a + 1} \right)t\end{array} \right.\) vuông góc với nhau?

A. \[a =  - 2.\]                   B. \[a = 2.\]                   C. \[a =  - 1.\]                D. \[a = 1\].

Lời giải

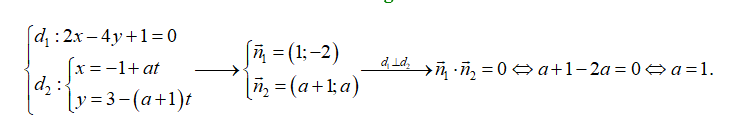
Chọn D

Câu 13:      Với giá trị nào của \(m\) thì hai đường thẳng

\({d_1}:\left\{ \begin{array}{l}x =  - 2 + 2t\\y =  - 3t\end{array} \right.\) và \({d_2}:\left\{ \begin{array}{l}x = 2 + mt\\y =  - 6 + \left( {1 - 2m} \right)t\end{array} \right.\) trùng nhau?

A. \(m = \frac{1}{2}\).     B. \(m =  - 2\).               C. \(m = 2\).                  D. \(m \ne  \pm 2\).

Lời giải

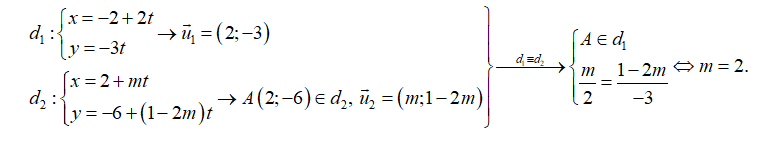
Chọn C

Câu 14:      Tìm tất cả các giá trị của \[m\] để hai đường thẳng

\[{d_1}:\left\{ {\begin{array}{*{20}{c}}{x = 2 + 2t}\\{y = 1 + mt}\end{array}} \right.\] và \[{d_2}:4x - 3y + m = 0\] trùng nhau.

A. \[m =  - 3\].                 B. \[m = 1\].                  C. \[m = \frac{4}{3}\].   D. \(m \in \emptyset \).

Lời giải

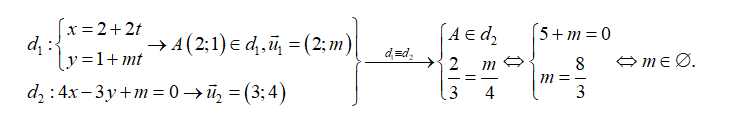
Chọn D

Câu 15:      Với giá trị nào của \(m\) thì hai đường thẳng

\({d_1}:2x + y + 4 - m = 0\) và \({d_2}:\left( {m + 3} \right)x + y + 2m - 1 = 0\) song song?

A. \(m = 1.\)                     B. \(m =  - 1.\)               C. \(m = 2.\)                  D. \(m = 3.\)

Lời giải

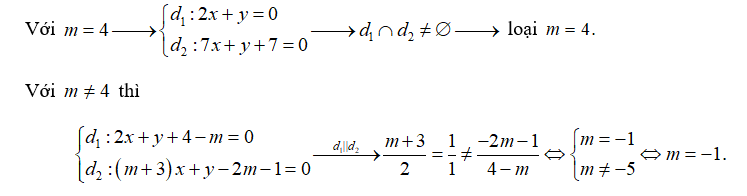
Chọn B

Câu 16:      Tìm tất cả các giá trị của \[m\] để hai đường thẳng

\[{\Delta _1}:2x - 3my + 10 = 0\] và \[{\Delta _2}:mx + 4y + 1 = 0\] cắt nhau.

A. \[1 < m < 10\].            B. \[m = 1\].                  C. Không có \[m\].        D. Với mọi \[m\].

Lời giải

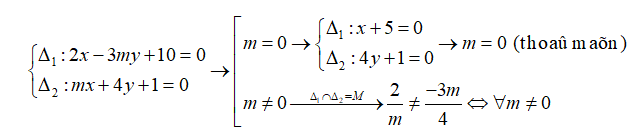
Chọn D

Câu 17:      Với giá trị nào của \(m\) thì hai đường thẳng

\[{\Delta _1}:mx + y - 19 = 0\] và \[{\Delta _2}:\left( {m - 1} \right)x + \left( {m + 1} \right)y - 20 = 0\] vuông góc?

A. Với mọi \(m\).             B. \(m = 2\).                  C. Không có \(m\).        D. \(m =  \pm 1\).

Lời giải

Ta có :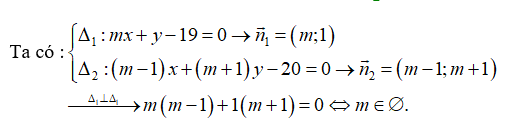 

Câu 18:      Với giá trị nào của \[m\] thì hai đường thẳng

\[{d_1}:3mx + 2y + 6 = 0\] và \[{d_2}:\left( {{m^2} + 2} \right)x + 2my + 6 = 0\] cắt nhau?

A. \[m \ne  - 1\].              B. \[m \ne 1\].               C. \(m \in \mathbb{R}\).                                        D. \[m \ne 1\;{\rm{ v\`a  }}\;m \ne  - 1\].

Ta có: \[\left\{ \begin{array}{l}{d_1}:3mx + 2y + 6 = 0 \to {{\vec n}_1} = \left( {3m;2} \right)\\{d_2}:\left( {{m^2} + 2} \right)x + 2my + 6 = 0 \to {{\vec n}_2} = \left( {{m^2} + 2;2m} \right)\end{array} \right.\]

 Chọn D

Câu 19:      Với giá trị nào của \[m\] thì hai đường thẳng

\[{d_1}:2x - 3y - 10 = 0\] và \[{d_2}:\left\{ {\begin{array}{*{20}{c}}{x = 2 - 3t}\\{y = 1 - 4mt}\end{array}} \right.\] vuông góc?

A. \[m = \frac{1}{2}\].     B. \[m = \frac{9}{8}\].   C. \[m =  - \frac{9}{8}\].                                        D. \(m =  - \frac{5}{4}\).

Lời giải

\[\left\{ \begin{array}{l}{d_1}:2x - 3y - 10 = 0 \to {{\vec n}_1} = \left( {2; - 3} \right)\\{d_2}:\left\{ {\begin{array}{*{20}{c}}{x = 2 - 3t}\\{y = 1 - 4mt}\end{array} \to {{\vec n}_2} = \left( {4m; - 3} \right)} \right.\end{array} \right.\]

 Chọn C

Câu 20:      Với giá trị nào của \[m\] thì hai đường thẳng

\[{d_1}:4x - 3y + 3m = 0\] và \[{d_2}:\left\{ {\begin{array}{*{20}{c}}{x = 1 + 2t}\\{y = 4 + mt}\end{array}} \right.\] trùng nhau?

A. \[m =  - \frac{8}{3}\].  B. \[m = \frac{8}{3}\].   C. \[m =  - \frac{4}{3}\].                                        D. \[m = \frac{4}{3}\].

Lời giải

\[\left\{ \begin{array}{l}{d_1}:4x - 3y + 3m = 0 \to {{\vec n}_1} = \left( {4; - 3} \right)\\{d_2}:\left\{ {\begin{array}{*{20}{c}}{x = 1 + 2t}\\{y = 4 + mt}\end{array} \to A\left( {1;4} \right) \in {d_2},\,\,{{\vec n}_2} = \left( {m; - 2} \right)} \right.\end{array} \right.\]

 Chọn B

Câu 21:      Với giá trị nào của \[m\] thì hai đường thẳng

\[{d_1}:3mx + 2y - 6 = 0\] và \[{d_2}:\left( {{m^2} + 2} \right)x + 2my - 3 = 0\] song song?

A. \[m = 1;\,\,m =  - 1.\]   B. \(m \in \emptyset \).                                      C. \[m = 2\].                         D. \[m =  - 1\].

Lời giải

Ta có

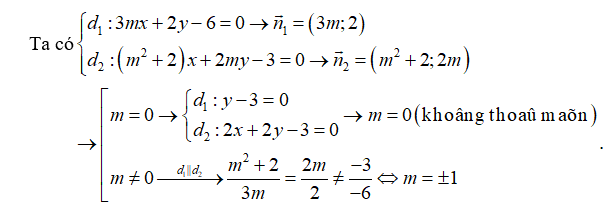
Câu 22:      Với giá trị nào của \[m\] thì hai đường thẳng

\[{d_1}:\left\{ \begin{array}{l}x = 8 - \left( {m + 1} \right)t\\y = 10 + t\end{array} \right.\] và \[{d_2}:mx + 2y - 14 = 0\] song song?

A. \[\left[ \begin{array}{l}m = 1\\m =  - 2\end{array} \right.\].                B. \[m = 1\].                         C. \[m =  - 2\].               D. \(m \in \emptyset \).

Lời giải

Ta có:\[\left\{ \begin{array}{l}{d_1}:\left\{ \begin{array}{l}x = 8 - \left( {m + 1} \right)t\\y = 10 + t\end{array} \right. \to A\left( {8;10} \right) \in {d_1},\,\,{{\vec n}_1} = \left( {1;m + 1} \right)\\{d_2}:mx + 2y - 14 = 0 \to {{\vec n}_2} = \left( {m;2} \right)\end{array} \right.\]

 Chọn A

Câu 23:      Với giá trị nào của \[m\] thì hai đường thẳng

\[{d_1}:\left( {m - 3} \right)x + 2y + {m^2} - 1 = 0\] và \[{d_2}: - x + my + {m^2} - 2m + 1 = 0\] cắt nhau?

A. \[m \ne 1\].                 B. \[\left\{ \begin{array}{l}m \ne 1\\m \ne 2\end{array} \right.\].     C. \[m \ne 2\].               D. \[\left[ \begin{array}{l}m \ne 1\\m \ne 2\end{array} \right.\].

Lời giải

\[\left\{ \begin{array}{l}{d_1}:\left( {m - 3} \right)x + 2y + {m^2} - 1 = 0\\{d_2}: - x + my + {m^2} - 2m + 1 = 0\end{array} \right.\]

 Chọn B