Tài liệu chuyên đề Tính xác suất theo định nghĩa cổ điển Toán lớp 10 sách Kết nối tri thức gồm lý thuyết và các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Toán 10. 

Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Toán 10 Kết nối tri thức word có lời giải chi tiết:

B1: Gửi phí vào tài khoản0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây

Xem thử tài liệu tại đây: Link tài liệu

Chuyên đề Tính xác suất theo định nghĩa cổ điển

Tài liệu gồm 4 Chuyên đề nhỏ, mời bạn đọc xem thử nội dung Chuyên đề Biến cố và định nghĩa cổ điển của xác suất  :

Chuyên đề 2: BIẾN CỐ VÀ ĐỊNH NGHĨA CỔ ĐIỂN CỦA XÁC SUẤT

I. BIẾN CỐ

1. Phép thử ngẫu nhiên (gọi tắt là phép thử) là một phép thử mà ta không đoán trước được kết quả của nó, mặc dù đã biết tập hợp tất cả các kết quả có thể có của phép thử đó.

2. Không gian mẫu

Tập hợp các kết quả có thể xẩy ra của một phép thử được gọi là không gian mẫu của phép thử đó và ký hiệu là \(\Omega \).

Ví dụ: Khi ta tung một đồng xu có 2 mặt, ta hoàn toàn không biết trước được kết quả của nó, tuy nhiên ta lại biết chắc chắn rằng đồng xu rơi xuống sẽ ở một trong 2 trạng thái: sấp (S) hoặc ngửa (N).

Không gian mẫu của phép thử là \(\Omega  = \left\{ {S;\,N} \right\}\)

3. Một biến cố \(A\)(còn gọi là sự kiện \[A\]) liên quan tới phép thử \[T\] là biến cố mà việc xẩy ra hay không xẩy ra của nó còn tùy thuộc vào kết quả của \[T\].

Mỗi kết quả của phép thử \[T\]làm cho biến cố \[A\] xảy ra được gọi là một kết quả thuận lợi cho \[A\].

4. Tập hợp các kết quả thuận lợi cho \[A\] được kí hiệu bởi \(n\left( A \right)\) hoặc \({\Omega _A}\). Để đơn giản, ta có thể dùng chính chữ \(A\) để kí hiệu tập hợp các kết quả thuận lợi cho \(A\).

Khi đó ta cũng nói biến cố \(A\) được mô tả bởi tập \(A\).

5. Biến cố chắc chắn là biến cố luôn xẩy ra khi thực hiện hiện phép thử \(T\). Biến cố chắc chắn được mô tả bởi tập \(\Omega \) và được ký hiệu là \(\Omega \).

6. Biến cố không thể là biến cố không bao giờ xẩy ra khi thực hiện phép thử \(T\). Biến cố không thể được mô tả bởi tập \(\emptyset \).

7. Các phép toán trên biến cố

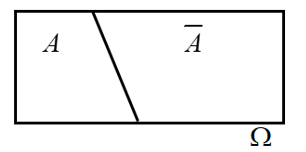
* Tập \(\Omega \backslash A\) được gọi là biến cố đối của biến cố \(A\), kí hiệu là \(\overline A \). Giả sử \(A\) và \(B\) là hai biến cố liên quan đến một phép thử. Ta có:

* Tập \(A \cup B\) được gọi là hợp của các biến cố \(A\) và \(B\).

* Tập \(A \cap B\) được gọi là giao của các biến cố \(A\) và \(B\).

* Nếu \(A \cap B = \emptyset \) thì ta nói \(A\) và \(B\) xung khắc.

8. Bảng đọc ngôn ngữ biến cố.

II. ĐỊNH NGHĨA CỔ ĐIỂN CỦA XÁC SUẤT

1. Định nghĩa cổ điển của xác suất:

Cho \(T\) là một phép thử ngẫu nhiên với không gian mẫu \(\Omega \) là một tập hữu hạn. Giả sử \(A\) là một biến cố được mô ta bằng \({\Omega _A} \subset \Omega \). Xác suất của biến cố \(A\),  kí hiệu bởi \(P(A)\), được cho bởi công thức

\(P(A) = \frac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \frac{{\left| {{\Omega _A}} \right|}}{{\left| \Omega  \right|}} = \).

Chú ý:

\( \bullet \) \(0 \le P(A) \le 1\).

\( \bullet \) \(P(\Omega ) = 1,{\rm{ }}P(\emptyset ) = 0\).

2. Định nghĩa thống kê của xác suất

Xét phép thử ngẫu nhiên T và một biến cố A liên quan tới phép thử đó. Nếu tiến hành lặp đi lặp lại N lần phép thử T và thống kê số lần xuất hiện của A là n.

Khi đó xác suất của biến cố A được định nghĩa như sau:

.

III. CÁC QUY TẮC TÍNH XÁC SUẤT

     1. Quy tắc cộng

a) Quy tắc cộng xác suất

* Nếu hai biến cố \[A,B\] xung khắc nhau thì

\(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\)

* Nếu các biến cố \[{A_1},{A_2},{A_3},...,{A_k}\] xung khắc nhau thì

\(P\left( {{A_1} \cup {A_2} \cup ... \cup {A_k}} \right) = P\left( {{A_1}} \right) + P\left( {{A_2}} \right) + ... + P\left( {{A_k}} \right)\)

b) Công thức tính xác suất biến cố đối

Xác suất của biến cố \[\overline A \] của biến cố \[A\] là

\(P\left( {\overline A } \right) = 1 - P\left( A \right)\)

2. Quy tắc nhân xác suất

Quy tắc nhân xác suất

Nếu \[A\] và \[B\] là hai biến cố độc lập thì

\[P\left( {AB} \right) = P\left( A \right).P\left( B \right)\]

Một cách tổng quát, nếu \(k\) biến cố \[{A_1},{A_2},{A_3},...,{A_k}\] là độc lập thì

\[P\left( {{A_1},{A_2},{A_3},...,{A_k}} \right) = P\left( {{A_1}} \right).P\left( {{A_2}} \right)...P\left( {{A_k}} \right)\]

Chú ý:

* Nếu \[A\] và \[B\] độc lập thì \[A\] và \[\overline B \] độc lập, \[B\] và \[\overline A \] độc lập, \[\overline B \] và \[\overline A \] độc lập. Do đó Nếu \[A\] và \[B\] độc lập thì ta còn có các đẳng thức

                                      \[\begin{array}{l}P\left( {A\overline B } \right) = P\left( A \right).P\left( {\overline B } \right)\\P\left( {\overline A B} \right) = P\left( {\overline A } \right).P\left( B \right)\\P\left( {\overline A \overline B } \right) = P\left( {\overline A } \right).P\left( {\overline B } \right)\end{array}\]

* Nếu một trong các đẳng thức trên bị vi phạm thì hai biến cố \(A\) và \(B\) không độc lập với nhau

DẠNG 1 : MÔ TẢ BIẾN CỐ, KHÔNG GIAN MẪU

Câu 1 : Hãy mô tả không gian mẫu \[\Omega \] của phép thử :  « Gieo một con súc sắc » . Hãy mô tả biến cố A :  « Số chấm trên mặt xuất hiện là số lẻ »

Câu 2 : Hãy mô tả không gian mẫu \[\Omega \] khi tung ba đồng xu

Câu 3 : Hãy mô tả không gian mẫu khi thực hiện phép thử : Lấy ngẫu nhiên từng quả cầu đánh số 1 ;2 ;3 ra và xếp thành một hàng ngang để được một số có ba chữu số.

Câu 4 : Một hộp đựng \[10\]  thẻ, đánh số từ \[1\] đến \[10\]. Chọn ngẫu nhiên \[3\]  thẻ. Gọi \[A\] là biến cố để tổng số của \[3\] thẻ được chọn không vượt quá \[8\]. Tính số phần tử của biến cố \[A\]

Câu 5 : Gieo con súc sắc hai lần. Biến cố \[A\] là biến cố để sau hai lần gieo có ít nhất một mặt 6 chấm . Mô tả biến cố \[A\]

\[A = \left\{ {\left( {6,1} \right),\,\left( {6,2} \right),\,\left( {6,3} \right),\,\left( {6,4} \right),\,\left( {6,5} \right)} \right\}\].

Câu 6.Gieo 2 con súc sắc và gọi kết quả xảy ra là tích số hai nút ở mặt trên. Số phần tử của không gian mẫu là:

Câu 7.Một hộp đựng \[10\] thẻ, đánh số từ \[1\] đến \[10\]. Chọn ngẫu nhiên \[3\] thẻ. Gọi \[A\] là biến cố để tổng số của \[3\] thẻ được chọn không vượt quá \[8\]. Số phần tử của biến cố \[A\] là:

Câu 8.Gieo một đồng tiền và một con súc sắc. Số phần tử của không gian mẫu là

Câu 9.Gieo ngẫu nhiên \[2\] đồng tiền thì không gian mẫu của phép thử có bao nhiêu phần tử?

Câu 10.Gieo một đồng tiền liên tiếp \(2\) lần. Số phần tử của không gian mẫu \[n(\Omega )\]là?

Câu 11.Gieo một con súc sắc \(2\) lần. Số phần tử của không gian mẫu là?

Câu 12.Gieo một đồng tiền liên tiếp \(3\) lần thì \[n(\Omega )\] là bao nhiêu?

DẠNG 2: MỐI LIÊN HỆ GIỮA CÁC BIẾN CỐ

Câu 1: Một lớp có 15 học sinh nam và 17 học sinh nữ. Gọi A là biến cố : “lập một đội văn nghệ của lớp gồm 7 học sinh trong đó nhất thiết phải có học sinh nữ”. Hãy mô tả biến cố đối của biến cố A (Giả thiết rằng học sinh nào cũng có khả năng văn nghệ)

Câu 2: Một xạ thủ bắn hai phát độc lập với nhau. Gọi \[{A_1},\,{A_2}\] lần lượt là biến cố lần thứ nhất và lần thứ 2 bắn trúng hồng tâm. Hãy biểu diễn các biến cố sau thông qua các biến cố \[{A_1},\,{A_2}\]

a.    Cả hai lần đều bắn trúng hồng tâm

b.   Cả hai lần không bắn trúng hồng tâm

c.    Ít nhất một lần bắn trúng hồng tâm

DẠNG 3: XÁC ĐỊNH KHÔNG GIAN MẪU VÀ BIẾN CỐ

Phương pháp 1: Liệt kê các phần tử của không gian mẫu và biến cố rồi đếm.

Phương pháp 2: Sử dụng các quy tắc đếm, các kiến thức về hoán vị, chỉnh hợp, tổ hợp để xác định số phần tử của không gian mẫu và biến cố.

Câu 1. Gieo một đồng xu cân đối và đồng chất liên tiếp cho đến khi lần đầu tiên xuất hiện mặt sấp hoặc cả năm lần ngửa thì dừng lại.

1. Mô tả không gian mẫu.

2. Xác định các biến cố:

A: “Số lần gieo không vượt quá ba”

B: “Có ít nhất 2 lần gieo xuất hiện mặt ngửa”

Câu 2. Trong một chiếc hộp đựng 6 viên bi đỏ, 8 viên bi xanh, 10 viên bi trắng. Lấy ngẫu nhiên 4 viên bi. Tính số phần tử của

1. Không gian mẫu

2. Các biến cố:

a) A: “ 4 viên bi lấy ra có đúng hai viên bi màu trắng”.

b) B: “ 4 viên bi lấy ra có ít nhất một viên bi màu đỏ”.

c) C: “ 4 viên bi lấy ra có đủ 3 màu”.

Câu 3. Chọn ngẫu nhiên một số tự nhiên có 4 chữ số đôi một khác nhau. Tính số phần tử của

1. Không gian mẫu.

2. Các biến cố

a) A: “Số được chọn chia hết cho 5”

b) B: “Số được chọn có đúng 2 chữ số lẻ và và hai chữ số lẻ không đứng kề nhau”

Câu 4. Một xạ thủ bắn liên tục 4 phát đạn vào bia. Gọi Ak là các biến cố “ xạ thủ bắn trúng lần thứ với . Hãy biểu diễn các biến cố sau qua các biến cố.

A: "Lần thứ tư mới bắn trúng bia".

B: "Bắn trúng bia ít nhất một lần".

C: "Bắn trúng bia đúng ba lần".

Câu 5. Có 100 tấm thẻ được đánh số từ 1 đến 100. Lấy ngẫu nhiên 5 thẻ. Tính số phần tử của

1. Không gian mẫu

2. Các biến cố:

   a)  A: “Số ghi trên các tấm thẻ được chọn đều là số chẵn”.

   b)  B: “Có ít nhất một số ghi trên thẻ được chọn chia hết cho 3”.