Tài liệu chuyên đề Bất phương trình và hệ bất phương trình bậc nhất hai ẩn Toán lớp 10 sách Kết nối tri thức gồm lý thuyết và các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Toán 10. 

Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Toán 10 Kết nối tri thức word có lời giải chi tiết:

B1: Gửi phí vào tài khoản0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây

Xem thử tài liệu tại đây: Link tài liệu

Chuyên đề Bất phương trình và hệ bất phương trình bậc nhất hai ẩn

Tài liệu gồm 4 Chuyên đề nhỏ, mời bạn đọc xem thử nội dung Chuyên đề Hệ bất phương trình bậc nhất hai ẩn :

Chuyên đề 2: HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN.

I. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Tương tự hệ bất phương trình một ẩn

Hệ bất phương trình bậc nhất hai ẩn gồm một số bất phương trình bậc nhất hai ẩn \[x,\,\,y\] mà ta phải tìm các nghiệm chung của chúng. Mỗi nghiệm chung đó được gọi là một nghiệm của hệ bất phương trình đã cho.

Cũng như bất phương trình bậc nhất hai ẩn, ta có thể biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn.

II. BIỂU DIỄN TẬP NGHIỆM CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Để biểu diễn miền nghiệm của hệ bất phương trình bậc nhất 2 ẩn ta làm nư sau:

- Trong cùng hệ toạ độ, biểu diễn miền nghiệm của mỗi bất phương trình trong hệ bằng cách gạch bỏ phần không thuộc miền nghiệm của nó.

- Phần không bị gạch là miền nghiệm cần tìm.

III. ÁP DỤNG VÀO BÀI TOÁN THỰC TIỄN

Giải một số bài toán kinh tế thường dẫn đến việc xét những hệ bất phương trình bậc nhất hai ẩn và giải chúng. Loại bài toán này được nghiên cứu trong một ngành toán học có tên gọi là Quy hoạch tuyến tính.

2.4. Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?

                                 a) \(\left\{ {\begin{array}{*{20}{c}}{x < 0}\\{y \ge 0;}\end{array}} \right.\)                           b) \(\left\{ {\begin{array}{*{20}{c}}{x + {y^2} < 0}\\{y - x > 1;}\end{array}} \right.\)                            c) \(\left\{ {\begin{array}{*{20}{c}}{x + y + z < 0}\\{y < 0;\quad \quad \;\,}\end{array}} \right.\)           d) \(\left\{ {\begin{array}{*{20}{c}}{ - 2x + y < {3^2}}\\{{4^2}x + 3y < 1.}\end{array}} \right.\)

Lời giải

a) \(\left\{ {\begin{array}{*{20}{c}}{x < 0}\\{y \ge 0;}\end{array}} \right.\)                 d) \(\left\{ {\begin{array}{*{20}{c}}{ - 2x + y < {3^2}}\\{{4^2}x + 3y < 1.}\end{array}} \right.\)

2.5. Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau trên mặt phẳng tọa độ:

a) \(\left\{ {\begin{array}{*{20}{c}}{y - x <  - 1}\\{x > 0\quad \;\;\;\,}\\{y < 0;\quad \quad }\end{array}} \right.\)                           b) \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0\quad \quad }\\{y \ge 0\quad \quad }\\{2x + y \le 4;}\end{array}} \right.\)                                          c) \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0\quad \;}\\{x + y > 5}\\{x - y < 0.}\end{array}} \right.\)

Lời giải

a) \(\left\{ {\begin{array}{*{20}{c}}{y - x <  - 1}\\{x > 0\quad \;\;\;\,}\\{y < 0;\quad \quad }\end{array}} \right.\)

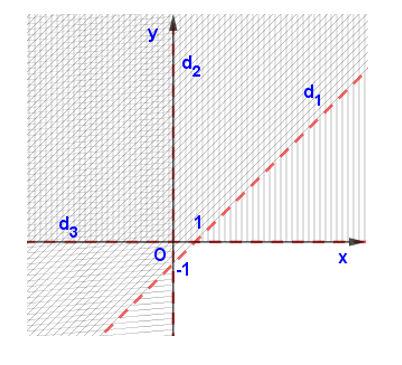
Bước 1: Vẽ đường thẳng \(\left( {{d_1}} \right): - x + y =  - 1\)

               Vì \( - 0 + 0 = 0 >  - 1\) nên tọa độ điểm \(O\left( {0;0} \right)\)không thỏa mãn bất phương trình \( - x + y <  - 1\)

                Do đó miền nghiệm của của bất phương trình\( - x + y <  - 1\) là nửa mặt phẳng bờ \({d_1}\) không chứa gốc tọa độ \(O\) không kể đường thẳng \({d_1}\).

Bước 2: Vẽ đường thẳng \(\left( {{d_2}} \right):x = 0\)

               Vì \(1 > 0\) nên tọa độ điểm \(\left( {1;0} \right)\)thỏa bất phương trình \(x > 0\)

               Do đó miền nghiệm của bất phương trình \(x > 0\)là nửa mặt phẳng bờ \(Oy\)chứa điểm \(\left( {1;0} \right)\)không kể bờ \(Oy\).

Bước 3: Vẽ đường thẳng \(\left( {{d_3}} \right):y = 0\)

               Vì \( - 1 < 0\) nên tọa độ điểm \(\left( {0, - 1} \right)\)thỏa bất phương trình \(y < 0\)

               Do đó miền nghiệm của bất phương trình \(y < 0\)là nửa mặt phẳng bờ \(Ox\)chứa điểm \(\left( {0; - 1} \right)\)không kể bờ \(Ox\).

Vậy miền nghiệm của hệ là miền không bị gạch.

b) \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0\quad \quad }\\{y \ge 0\quad \quad }\\{2x + y \le 4;}\end{array}} \right.\)

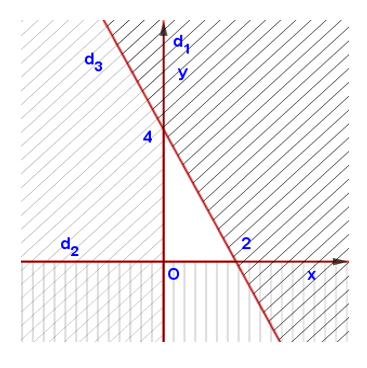
Bước 1: Vẽ đường thẳng \(\left( {{d_1}} \right):x = 0\)

               Vì \(1 > 0\) nên tọa độ điểm \(\left( {1;0} \right)\)thỏa bất phương trình \(x \ge 0\)

               Do đó miền nghiệm của bất phương trình \(x \ge 0\)là nửa mặt phẳng bờ \(Oy\) và đường thẳng \(x = 0\) chứa điểm \(\left( {1;0} \right)\).

Bước 2: Vẽ đường thẳng \(\left( {{d_2}} \right):y = 0\)

               Vì \(1 > 0\) nên tọa độ điểm \(\left( {0,1} \right)\)thỏa bất phương trình \(y \ge 0\)

               Do đó miền nghiệm của bất phương trình \(y \ge 0\)là nửa mặt phẳng bờ \(Ox\) và đường thẳng \(y = 0\)chứa điểm \(\left( {0;1} \right)\).

Bước 3: Vẽ đường thẳng \(\left( {{d_3}} \right):2x + y = 4\)

               Vì \(2.0 + 0 = 0 < 4\) nên tọa độ điểm \(O\left( {0;0} \right)\) thỏa mãn bất phương trình \(2x + y \le 4\)

                Do đó miền nghiệm của của bất phương trình\(2x + y \le 4\) là nửa mặt phẳng bờ \({d_3}\) và đường thẳng \(2x + y = 4\)chứa gốc tọa độ \(O\).

Vậy miền nghiệm của hệ là miền không bị gạch.

2.6. Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilôgam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilôgam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn; giá tiền 1 kg thịt bò là 250 nghìn đồng; 1 kg thịt lợn là 160 nghìn đồng. Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn.

a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm của hệ đó.

b) Gọi F (nghìn đồng) là số tiền phải trả cho x kilôgam thịt bò và y kilôgam thịt lợn. Hãy biểu diễn F theo x và y.

c) Tìm số kilôgam thịt mỗi loại mà gia đình cần mua để chi phí là ít nhất.

Lời giải

a) Gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giả sử gia đình này mua x kilôgam thịt bò và y kilôgam thịt lợn thì x và y cần thỏa mãn điều kiện:

\(0 \le x \le 1,6\) và \(0 \le y \le 1,1\).

Gia đình này cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày nên điều kiện tương ứng là

\(800x + 600y \ge 900\)và \(200x + 400y \ge 400\)

Hay \(8x + 6y \ge 9\) và \(x + 2y \ge 2\)

Từ các bất phương trình biểu thị các điều kiện của bài toán, ta có hệ bất phương trình sau:

\(\left\{ {\begin{array}{*{20}{c}}{0 \le x \le 1,6\,}\\{0 \le y \le 1,1\,}\\{8x + 6y \ge 9}\\{x + 2y \ge 2\,}\end{array}} \right.\)

Biểu diễn miền nghiệm của hệ bất phương trình:

\(\begin{array}{l}\left( {{d_1}} \right):x = 1,6\\\left( {{d_2}} \right):y = 1,1\\\left( {{d_3}} \right):8x + 6y = 9\\\left( {{d_4}} \right):x + 2y = 2\end{array}\)

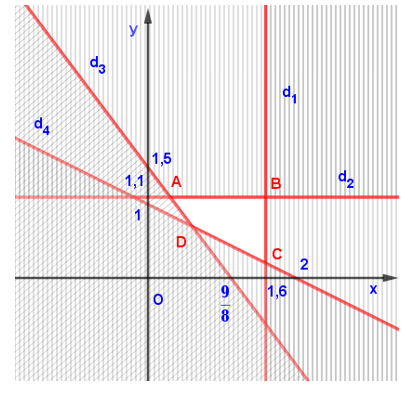
Miền nghiệm của hệ trên là miền tứ giác ABCD

(kể cả biên).

b) \(F = 250x + 160y\)(nghìn đồng)

c) \(F\left( {x;y} \right)\)đạt giá trị lớn nhất hoặc nhỏ nhất tại một trong các đỉnh của tứ giác ABCD.

\(A \in \left( {{d_2}} \right) \cap \left( {{d_3}} \right) \Rightarrow A\left( {0,3;1,1} \right)\), ta có \(F\left( {0,3;1,1} \right) = 250.0,3 + 160.0,1 = 91\)(nghìn đồng)

\(B \in \left( {{d_1}} \right) \cap \left( {{d_2}} \right) \Rightarrow B\left( {1,6;1,1} \right)\), ta có \(F\left( {1,6;1,1} \right) = 250.1,6 + 160.1,1 = 576\)(nghìn đồng)

\(C \in \left( {{d_1}} \right) \cap \left( {{d_4}} \right) \Rightarrow C\left( {1,6;0,2} \right)\), ta có \(F\left( {1,6;0,2} \right) = 250.1,6 + 160.0,2 = 432\)(nghìn đồng)

\(D \in \left( {{d_3}} \right) \cap \left( {{d_4}} \right) \Rightarrow D\left( {0,6;0,7} \right)\), ta có \(F\left( {0,6;0,7} \right) = 250.0,6 + 160.0,7 = 262\)(nghìn đồng)

Vậy gia đình đó cần mua \(0,3\)kg thịt bò và \(1,1\)kg thịt lợn để chi phí là ít nhất.