Tailieumoi.vn xin giới thiệu Đề cương ôn tập giữa kì 2 Toán 7 Chân trời sáng tạo năm 2024 – 2025. Tài liệu được biên soạn bởi đội ngũ giáo viên THPT dày dặn kinh nghiệm sẽ giúp các em làm quen với các dạng bài tập, nâng cao kỹ năng làm bài và rút kinh nghiệm cho bài thi Giữa học kì 2 Toán 7. Mời các bạn cùng đón xem:
Đề cương ôn tập giữa kì 2 Toán 7 Chân trời sáng tạo năm 2025
*Chương 6. Các đại lượng tỉ lệ
- Nhận biết tỉ lệ thức và các tính chất của tỉ lệ thức.
- Nhận biết tính chất của dãy tỉ số bằng nhau.
- Hiểu rõ định nghĩa, tính chất để lập được tỉ lệ thức.
- Sử dụng tính chất của tỉ lệ thức và dãy tỉ số bằng nhau để tính toán.
- Chứng minh đẳng thức dựa vào tính chất của tỉ lệ thức và dãy tỉ số bằng nhau.
- Vận dụng được tính chất của đại lượng tỉ lệ thuận, tỉ lệ nghịch để tìm giá trị của một đại lượng và toán chia tỉ lệ.
*Chương 8. Tam giác
- Nhận biết hai tam giác bằng nhau.
- Chứng minh hai tam giác bằng nhau theo các trường hợp.
- Tìm số đo của góc, độ dài của cạnh trong tam giác.
- Chứng minh ba điểm thẳng hàng dựa vào các dữ kiện về góc.
- Xác định loại tam giác dựa vào các dữ kiện về góc và cạnh.
- Giải thích được tính chất của tam giác cân (hai cạnh bên bằng nhau, hai góc ở đáy bằng nhau).
- Tìm độ dài cạnh và số đo góc dựa điều kiện của tam giác.
- Nhận biết khái niệm đường vuông góc và đường xiên, khoảng cách từ một điểm đến một đường thẳng.
- Nhận biết quan hệ giữa đường vuông góc và đường xiên dựa trên mối quan hệ giữa cạnh và góc đối diện trong tam giác (đối diện với cạnh lớn hơn là góc lớn hơn và ngược lại)
A. TRẮC NGHIỆM
Bài 1: Biết các cạnh của một tam giác tỉ lệ với 3; 4; 5 và chu vi của nó là 36cm. Tính các cạnh của tam giác đó
A. 9cm; 12cm; 15cm
B. 10cm; 12cm; 14cm
C. 8cm; 12cm; 16cm
D. 8cm; 10cm; 18cm
Bài 2: Học sinh của ba lớp 6 cần phải trồng và chăm sóc 48 cây xanh. Lớp 6A có 28 học sinh, lớp 6B có 32 học sinh, lớp 6C có 36 học sinh. Hỏi mỗi lớp phải trồng và chăm sóc bao nhiêu cây xanh biết số học sinh tỉ lệ với số cây xanh?
A. 14; 15 và 19
B. 15; 16 và 17
C. 14; 16 và 18
D. 13; 16 và 19
Bài 3: 4m dây đồng nặng 23g. Hỏi 8km dây đồng như thế nặng bao nhiêu kg?
A. 11,5 kg
B. 34,5 kg
C. 46kg
D. 69kg
Bài 4: Ba đơn vị kinh doanh góp vốn theo tỉ lệ 3: 4: 5. Hỏi mỗi đơn vị được chia bao nhiêu tiền lãi nếu tổng số tiền lãi là 600 triệu đồng và tiền lãi được chia tỉ lệ thuận với số vốn đã đóng?
A. 120; 200 và 280
B. 130; 200 và 270
C. 140; 200 và 260
D. 150; 200 và 250
Bài 5: Biết độ dài các cạnh của một tam giác tỉ lệ với 4: 5: 6 . Tính độ dài mỗi cạnh của tam giác đó, biết rằng cạnh lớn nhất dài hơn cạnh nhỏ nhất là 8cm.
A. 16; 20 và 24
B. 18; 20 và 26
C. 20; 24 và 28
D. 20; 22 và 28
Bài 6: Trên một chiếc đồng hồ, khi kim giờ quay đúng năm vòng thì số vòng kim phút quay được là:
A. 15
B. 36
C. 60
D. 300
Bài 7: Cho x và y là hai đại lượng tỉ lệ thuận. Khi các giá trị x1, x2 của x có tổng bằng 4 thì giá trị tương ứng y1, y2 có tổng bằng – 8 . Tính giá trị của y khi x = - 2
A. – 1
B. 1
C. – 4
D. 4
Bài 8: Chu vi của một hình chữ nhật là 48cm. Tính độ dài mỗi cạnh biết chúng tỉ lệ với 3 và 5
A. 9cm và 15cm
B. 8cm và 16cm
C. 10cm và 14cm
D. 11cm và 13cm
Bài 9: Gọi x, y, z theo thứ tự là số vòng quay của kim giờ, kim phút và kim giây trong cùng một thời gian. Tìm hệ số tỉ lệ của z đối với x
A. 60
B. 120
C. 360
D. 720
Bài 10: Biết rằng 16l xăng nặng 12kg. Hỏi 10,5kg xăng có chứa được hết vào chiếc can bao nhiêu lít?
A. 11(l)
B. 12 (l)
C. 13 (l)
D. 14(l)
Bài 11: Một đội thợ gồm 35 người ăn hết số gạo được phân phát trong 68 ngày. Hỏi 28 người ăn hết số gạo đó trong mấy ngày?
A. 50 ngày
B. 65 ngày
C. 85 ngày
D. 100 ngày
Bài 12: Cho biết ba máy cày, cày xong một cánh đồng hết 35 giờ. Hỏi năm máy cày như thế (cùng năng suất) cày xong cánh đồng đó hết bao nhiêu giờ?
A. 12 giờ
B. 15 giờ
C. 18 giờ
D. 21 giờ
Bài 13 Trong các khẳng định sau, khẳng định nào đúng?
A. Nếu hai đại lượng tỉ lệ thuận với nhau thì tích hai giá trị tương ứng luôn không đổi
B. Nếu hai đại lượng tỉ lệ nghịch với nhau thì tỉ số hai giá trị bất kì của đại lượng này bằng tỉ số giữa hai giá trị tương ứng của đại lượng kia.
C. Cho x và y là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ là 3. Khi đó, với x = 3 thì y = 1
D. Nếu hai đại lượng tỉ lệ thuận với nhau thì tỉ số hai giá trị bất kì của đại lượng này bằng nghịch đảo của tỉ số giữa hai giá trị tương ứng của đại lượng kia.
Bài 14: Một xe máy chạy từ A đến B với vận tốc 45 km/h hết 3 giờ. Hỏi xe máy đó chạy từ A đến B với vận tốc 60 km/h sẽ hết bao nhiêu thời gian?
A. 2 giờ 25 phút
B. 2 giờ 15 phú
C. 2,15 giờ
D. 2 giờ
Bài 15: Giá trị của biểu thức x3 + 2x2 - 3 tại x = 2 là
A. 13
B. 10
C. 19
D. 9
Bài 15: Cho biểu thức đại số A = x2 - 3x + 8. Giá trị của A tại x = -2 là:
A. 13
B. 18
C. 19
D. 9
Bài 17: Cho biểu thức đại số B = x3 + 6x - 35. Giá trị của B tại x = 3, y = -4 là:
A. 16
B. 86
C. -32
D. -28
Bài 18: Cho A = 4x2y - 5 và B = 3x2y + 6 x2y2 + 3xy2. So sánh A và B khi x = -1, y = 3
A. A > B
B. A = B
C. A < B
D. A ≥ B
Bài 19: Tính giá trị biểu thức B = 5x2 -2x - 18 tại |x| = 4
A. B = 54
B. B = 70
C. B = 54 hoặc B = 70
D. B = 45 hoặc B = 70
Bài 20: So sánh giá trị của biểu thức M = tại x = 1 và y = - 2 với 1.
A. M = 1
B. M > 1
C. M < 1
D. M ≤ 1
Câu 21 Cho ABCD là hình chữ nhật như hình vẽ, điểm E nằm trên cạnh CD. Khẳng định nào sau đây là sai?
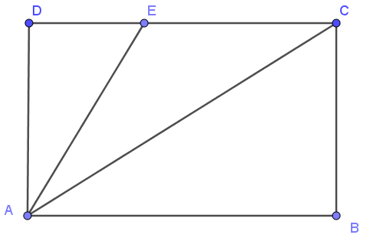
A. AE < AD;
B. AC > AD;
C. AC > AE;
D. AD < AE.
Câu 22. Điền vào chỗ trống sau: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó”.
A. Trung trực;
B. Giao điểm;
C. Trọng tâm;
D. Trung điểm.
B. PHẦN TỰ LUẬN
Bài 1. Cho hai đa thức: P(x) = x3 – 2x2 + x – 2;
Q(x) = 2x3 – 4x2 + 3x – 6.
a) Tính P(x) – Q(x).
b) Chứng tỏ rằng x = 2 là nghiệm của cả hai đa thức P(x) và Q(x).
Bài 2. Cho tỉ lệ thức . Chứng minh rằng
Bài 3. Tìm số hữu tỉ x trong các tỉ lệ thức sau:
c)
Bài 4
a. Tìm hai số a, b biết rằng 2a = 5b và 3a + 4b = 46
b. Tìm ba số a, b, c biết rằng a : b : c = 2 : 4 : 5 và a + b - c = 3
Bài 5. Trong đợt quyên góp sách ủng hộ các bạn vùng cao, số sách mà ba lớp 7A, 7B, 7C quyên góp được tỉ lệ với ba số 5; 6; 8. Tính số sách cả ba lớp đã quyên góp, biết số sách lớp 7C quyên góp nhiều hơn số sách của lớp 7A quyên góp là 24 quyển.
Bài 6
Cho tam giác ABC (AB < AC) M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho AM = EM.
a. Chứng minh: ΔAMB = ΔMCE
b. Từ A kẻ AH vuông góc với BC. Trên tia đối của tia HA lấy điểm D sao cho HA = HD. Chứng minh: CE = BD
c. Tam giác AMD là tam giác gì? Vì sao?
Bài 7. Cho tam giác ABC có D là trung điểm của AC. Trên đoạn BD lấy điểm E sao cho BE = 2ED. Điểm F thuộc tia đối của tia DE sao BF = 2BE. Gọi K là trung điểm của CF và G là giao điểm của EK và AC. Chứng minh G là trọng tâm tam giác EFC.
Bài 8. Cho tam giác ABC có góc A = 400 , AB = AC. Gọi M là trung điểm của BC. Tính các góc của tam giác AMB và tam giác AMC.
Bài 9. Cho tam giác ABC có AB = AC. D, E thuộc cạnh BC sao cho BD = DE = EC. Biết AD = AE.
a. Chứng minh góc EAB = góc DAC.
b. Gọi M là trung điểm của BC. Chứng minh AM là phân giác của góc DAE.
c. Giả sử góc DAE = 600. Tính các góc còn lại của tam giác DAE.
Bài 10. Cho tam giác ABC có góc A = 900. Vẽ AD ⊥ AB (D, C nằm khác phía đối với AB) và AD = AB. Vẽ AE ⊥ AC (E, B nằm khác phía đối với AC) và AE = AC. Biết DE = BC. Tính góc BAC.
Bài 11. Cho ABC có AB = AC. Kẻ AE là phân giác của góc BAC (E thuộc BC). Chứng minh rằng:
a. ∆ABE = ∆ACE
b. AE là đường trung trực của đoạn thẳng BC.
Bài 12. Cho ABC có AB < AC. Kẻ tia phân giác AD của góc BAC (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC. Chứng minh rằng:
a. ∆BDF = ∆EDC.
b. BF = EC.
c. F, D, E thẳng hàng.
d. AD ⊥ FC
Bài 13. Cho góc nhọn xOy. Trên tia Ox, lấy 2 điểm A và C. Trên tia Oy lấy 2 điểm B và D sao cho OA = OB; OC = OD. (A nằm giữa O và C; B nằm giữa O và D).
a. Chứng minh ∆OAD = ∆OBC
b. So sánh 2 góc CAD và CBD.
Bài 14. Cho ΔABC vuông ở A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC.
a. Chứng minh ΔABC = ΔABD
b. Trên tia đối của tia AB, lấy điểm M. Chứng minh ΔMBD = ΔMBC.
PHẦN TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Thay tỉ số 1,25 : 3,45 bằng tỉ số giữa các số nguyên ta được
A. 12,5 : 34,5;
B. 29 : 65;
C. 25 : 69;
D. 1 : 3.
Câu 2. Biết y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2. Khi x = –3 thì giá trị của y bằng bao nhiêu?
A. –6;
B. 0;
C. –9;
D. –1.
Câu 3. Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = –12 thì y = 8. Khi x = 3 thì y bằng
A. –32;
B. 32;
C. –2;
D. 2.
Câu 4. Cho hình vẽ sau:
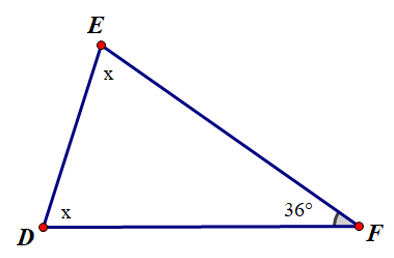
Số đo x là
A. 18°;
B. 72°;
C. 36°;
D. Không xác định được.
Câu 5. Hai tam giác bằng nhau là
A. Hai tam giác có ba cặp cạnh tương ứng bằng nhau;
B. Hai tam giác có ba cặp góc tương ứng bằng nhau;
C. Hai tam giác có ba cặp cạnh, ba cặp góc tương ứng bằng nhau;
D. Hai tam giác có hai cạnh bằng nhau.
Câu 6. Một tam giác cân có góc ở đáy bằng 40° thì số đo góc ở đỉnh là
A. 50°;
B. 40°;
C. 140°;
D. 100°.
Câu 7. Cho tam giác MNP có: MN < MP, MD ⊥ NP. Khẳng định nào sau đây là đúng?
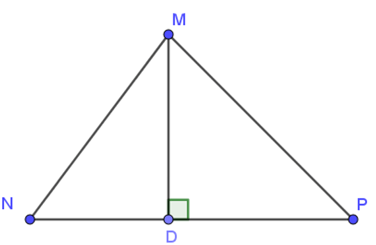
A. DN = DP;
B. MN = MP;
C. MD > MN;
D. MD < MP.
Câu 8. Điền vào chỗ trống sau: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó”.
A. Trung trực;
B. Giao điểm;
C. Trọng tâm;
D. Trung điểm.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1. (1,5 điểm) Tìm số hữu tỉ x trong các tỉ lệ thức sau:
c)
Bài 2. (2,0 điểm)
a. Tìm hai số a, b biết rằng 2a = 5b và 3a + 4b = 46
b. Tìm ba số a, b, c biết rằng a : b : c = 2 : 4 : 5 và a + b - c = 3
Bài 3. (1,5 điểm) Trong đợt quyên góp sách ủng hộ các bạn vùng cao, số sách mà ba lớp 7A, 7B, 7C quyên góp được tỉ lệ với ba số 5; 6; 8. Tính số sách cả ba lớp đã quyên góp, biết số sách lớp 7C quyên góp nhiều hơn số sách của lớp 7A quyên góp là 24 quyển.
Bài 4. (3,0 điểm)
Cho tam giác ABC (AB < AC) M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho AM = EM.
a. Chứng minh: ΔAMB = ΔMCE
b. Từ A kẻ AH vuông góc với BC. Trên tia đối của tia HA lấy điểm D sao cho HA = HD. Chứng minh: CE = BD
c. Tam giác AMD là tam giác gì? Vì sao?
Đáp án đề kiểm tra giữa kì 2 Toán 7
I. Trắc nghiệm
|
1. C |
2. A |
3. A |
4.B |
5. C |
6. D |
7. D |
8. D |
II. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm)
Vậy
Vậy
c.
3(x + 11) = 2(14 – x)
3x + 33 = 28 – 2x
3x + 2x = 28 – 33
5x = –5
x = –1
Vậy x = –1.
Bài 2. (1,5 điểm)
a) Ta có: 2a = 5b
Lại có:
=> 3a = 2. 15 = 30 => a = 10
4b = 2. 8 = 16 => b = 4.
b) a : b : c = 2 : 4 : 5
=> a = 2. 3 = 6
b = 4. 3 = 12
c = 5. 3 = 15
Bài 3. (1,5 điểm)
Gọi số sách 3 lớp 7A, 7B, 7C quyên góp được là x, y, z (quyển) ()
Vì số sách mà ba lớp 7A,7B,7C quyên góp được tỉ lệ với ba số 5;6;8 nên
Mà số sách lớp 7C quyên góp nhiều hơn số sách của lớp 7A quyên góp là 24 quyển nên z – x = 24
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
Vậy số sách 3 lớp 7A,7B,7C quyên góp được lần lượt là 40 quyển; 48 quyển và 64 quyển.
Bài 4. (3,0 điểm)
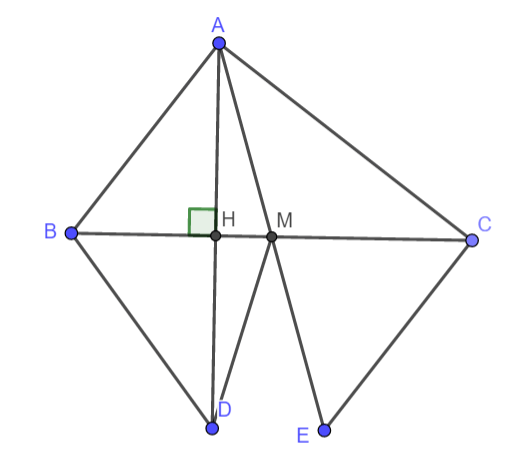
a. Xét tam giác ABM và tam giác MEC có:
BM = MC (M là trung điểm BC)
(đối đỉnh)
AM = ME (gt)
=> ΔAMB = ΔMCE (c - g - c)
b. Xét tam giác ABH vuông tại H và tam giác BHD vuông tại H có:
BH là cạnh chung
AH = DH (gt)
=> ΔABH = ΔBDH
=> AB = BD (1)
Ta lại có: ΔAMB = ΔMCE (cmt) => AB = CE (2)
Từ (1) và (2) suy ra CE = BD
c. Từ câu b ta dễ dàng suy ra MA = MD
Vậy tam giác AMD là tam giác cân tại M.